在算法30中,我们说过从左往右尝试模型,口诀就是针对固定集合,值不同,就是讨论要和不要的累加和。
那么对于非固定集合,我们应该怎么做呢?
针对非固定集合,面值固定,张数无限。口诀就是讨论要与不要,要的话逐步讨论要几张的累加和
题目:
* arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。
* 每个值都认为是一种面值,且认为张数是无限的。
* 返回组成aim的方法数
分析:
* 例如:arr = {1,2},aim = 4
* 方法如下:1+1+1+1、1+1+2、2+2 * 一共就3种方法,所以返回3
递归写法:
//递归版本public static int ways(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}return process(arr, 0, aim);}public static int process (int[] arr, int index, int aim){if (index == arr.length) { // 没钱了return aim == 0 ? 1 : 0;}//讨论不同货币组成aim的可能int ways = 0;//因为货币张数无限,所有需要讨论每一种情况。此次,就不是简单的要与不要的问题了for (int zhangshu = 0; zhangshu * arr[index] <= aim; zhangshu++) {/*** 此处,还是讨论要与不要的问题。* 0张代表不要* 要的话需要讨论要几张 :* 要1 张, 那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 要2 张,那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 依次类推*/ways += process(arr, index + 1, aim - zhangshu * arr[index]);}return ways;}动态规划
1. 套路还是老样子。以数组为横坐标,以aim为纵坐标。并且行与列都新增1个。
2. 根据递归
if (index == arr.length) { // 没钱了return aim == 0 ? 1 : 0;
}
可以推导出最后一行的第一列为1,其余全部为0.
| aim 0 | aim 1 | aim 2 | aim 3 | aim 4 | |
| index 0 (1) | |||||
| index 1 (2) | |||||
| index 2 | 1 | 0 | 0 | 0 | 0 |
3. 根据递归:
int ways = 0;
//因为货币张数无限,所有需要讨论每一种情况。此次,就不是简单的要与不要的问题了
for (int zhangshu = 0; zhangshu * arr[index] <= aim; zhangshu++) {/*** 此处,还是讨论要与不要的问题。* 0张代表不要* 要的话需要讨论要几张 :* 要1 张, 那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 要2 张,那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 依次类推*/ways += process(arr, index + 1, aim - zhangshu * arr[index]);
}
可以得到:
1. zhangshu * arr[index] <= aim必须成立,否则不做推导;直接返回0
2. 如果zhangshu * arr[index] <= aim成立,那么当前行当前列的值 依赖于下一行的aim - zhangshu * arr[index]列。
| aim= 0 | aim= 1 | aim= 2 | aim= 3 | aim= 4 | |
| index 0 (1) | |||||
| index 1 (2) | aim - zhangshu * arr[index] = 0 - 张数 *2; 讨论: 面值为2:张数为0,则 计算值为0 dp[1][0] = dp[2][0] = 1; 即只存在1种解法。 | 讨论: 张数为0 dp[1][1] = dp[2][1] = 0 张数为1 可得 1 - 2 < 0;取值0 0+0=0,最终取值0 | 讨论 张数0 dp[1][2] = dp[2][2] = 0; 张数为1,可得 2 - 2 =0; 可得dp[1][2] = dp[2][0] = 1; 张数为2,可得 2 - 2*2 <0;直接取0; 即1种解法,即0+1+0=1 | 讨论1: 张数为0 dp[1][3] ]= dp[2][3] = 0; 张数为1,可得 3 - 2 =1; 可得: dp[1][3] = dp[2][1] = 0; 张数为2。 可得3 - 2*2 < 0取值0; 张数为3. 即3-3*2<0,直接取0 0+0+0+0=0,最终取值0 | 张数为0, dp[1][4] = dp[2][4] = 0; 张数为1,可得 4 - 2 =2; dp[1][4] = dp[2][2] = 0; 张数为2. 可得4 - 2*2 = 0. dp[1][4] = dp[2][0] = 1; 张数为3: 4-3*2 < 0;直接取0 张数为4,4-4*2 < 0;直接取0 0+0+1+0+0=1 最终可得1种解法。 |
| index 2 | 1 | 0 | 0 | 0 | 0 |
接着,我们推导出第一行的数据:
| aim= 0 | aim= 1 | aim= 2 | aim= 3 | aim= 4 | |
| index 0 (1) | 面值为1 | 面值为1 张数为1: dp[0][1]=dp[1][0] = 1; 累计1种 | 张数为0: dp[0][2] = dp[1][2] = 1; 张数为1: dp[0][2] = dp[1][1] = 0; 累计1种 | 张数为0: dp[0][3] = dp[1][3] = 0; 张数为1: dp[0][3] = dp[1][2] = 1; 张数为2: dp[0][3] = dp[1][1] = 0; 累计1种 | 张数为0; dp[0][4]=[1][4-0] = dp[1][4] = 1 张数为1: dp[0][4] = dp[1][4-1*1] = dp[1][3] = 0; 张数为2: dp[0][4] = dp[1][4-2*1] = dp[1][2] = 1; 张数为3: dp[0][4] = dp[1][4-3*1] = dp[1][1] = 0; 张数为4: dp[0][4] = dp[1][4-4*1] = dp[1][0] = 1; 累计1+1+1=3; |
| index 1 (2) | aim - zhangshu * arr[index] = 0 - 张数 *2; 讨论: 面值为2:张数为0,则 计算值为0 dp[1][0] = dp[2][0] = 1; 即只存在1种解法。 | 讨论: 张数为0 dp[1][1] = dp[2][1] = 0 张数为1 可得 1 - 2 < 0;取值0 0+0=0,最终取值0 | 讨论 张数0 dp[1][2] = dp[2][2] = 0; 张数为1,可得 2 - 2 =0; 可得dp[1][2] = dp[2][0] = 1; 张数为2,可得 2 - 2*2 <0;直接取0; 即1种解法,即0+1+0=1 | 讨论1: 张数为0 dp[1][3] ]= dp[2][3] = 0; 张数为1,可得 3 - 2 =1; 可得: dp[1][3] = dp[2][1] = 0; 张数为2。 可得3 - 2*2 < 0取值0; 张数为3. 即3-3*2<0,直接取0 0+0+0+0=0,最终取值0
| 张数为0, dp[1][4] = dp[2][4] = 0; 张数为1,可得 4 - 2 =2; dp[1][4] = dp[2][2] = 0; 张数为2. 可得4 - 2*2 = 0. dp[1][4] = dp[2][0] = 1; 张数为3: 4-3*2 < 0;直接取0 张数为4,4-4*2 < 0;直接取0 0+0+1+0+0=1 最终可得1种解法。 |
| index 2 | 1 | 0 | 0 | 0 | 0 |
最终需要的是第一行最后一列数据:
1. aim为4,面值为1的一张都没有。可得dp[0][4]=[1][4-0] = dp[1][4] = 1
2. aim 为4, 面值为1的只有一张。可得 dp[0][4] = dp[1][4-1*1] = dp[1][3] = 0;
3. aim 为4, 面值为1的只有两张。可得 dp[0][4] = dp[1][4-2*1] = dp[1][2] = 1;
4. aim 为4, 面值为1的只有三张。可得 dp[0][4] = dp[1][4-3*1] = dp[1][1] = 0;
5. aim 为4, 面值为1的只有四张。可得 dp[0][4] = dp[1][4-4*1] = dp[1][0] = 1;
累计可得1+1+1 = 3, 即3种方法。
//动态规划public static int ways2(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}//老样子int N = arr.length;int[][] dp = new int[N + 1][aim + 1];//最后一行的第一列为1,其余都为0。 根据递归 return aim == 0 ? 1 : 0;得到dp[N][0] = 1;//双层for循环,动态规划的老套路。一维数组arr作为横坐标,aim作为纵坐标for (int row = N -1 ; row >= 0; row--) { //row代表递归中的 indexfor (int col = 0; col <= aim; col++) { //col代表递归中的 aim//此处是比较复杂的,完全套用递归内部的代码。这一层的for循环就是对//要的张数进行讨论。int ways = 0;//此处zhangshu * arr[row] <= col是唯一变化。重点理解for (int zhangshu = 0; zhangshu * arr[row] <= col; zhangshu++) {/*** 此处,还是讨论要与不要的问题。* 0张代表不要* 要的话需要讨论要几张 :* 要1 张, 那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 要2 张,那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 依次类推*///根据ways += process(arr, row + 1, aim - zhangshu * arr[row]);推导//此处的aim - zhangshu * arr[index] 需要变成 col - zhangshu * arr[index]ways += dp[row + 1][col - (zhangshu * arr[row])];}dp[row][col] = ways;}}return dp[0][aim];}那么如何进行时间复杂度优化呢?继续观察二维数组:
| aim= 0 | aim= 1 | aim= 2 | aim= 3 | aim= 4 | |
| index 0 (1) | 面值为1 | 面值为1 张数为1: dp[0][1]=dp[1][0] = 1; 累计1种 | 张数为0: dp[0][2] = dp[1][2] = 1; 张数为1: dp[0][2] = dp[1][1] = 0; 累计1种 | 张数为0: dp[0][3] = dp[1][3] = 0; 张数为1: dp[0][3] = dp[1][2] = 1; 张数为2: dp[0][3] = dp[1][1] = 0; 累计1种 | 张数为0; dp[0][4]=[1][4-0] = dp[1][4] = 1 张数为1: dp[0][4] = dp[1][4-1*1] = dp[1][3] = 0; 张数为2: dp[0][4] = dp[1][4-2*1] = dp[1][2] = 1; 张数为3: dp[0][4] = dp[1][4-3*1] = dp[1][1] = 0; 张数为4: dp[0][4] = dp[1][4-4*1] = dp[1][0] = 1; 累计1+1+1=3; |
| index 1 (2) | aim - zhangshu * arr[index] = 0 - 张数 *2; 讨论: 面值为2:张数为0,则 计算值为0 dp[1][0] = dp[2][0] = 1; 即只存在1种解法。 | 讨论: 张数为0 dp[1][1] = dp[2][1] = 0 张数为1 可得 1 - 2 < 0;取值0 0+0=0,最终取值0 | 讨论 张数0 dp[1][2] = dp[2][2] = 0; 张数为1,可得 2 - 2 =0; 可得dp[1][2] = dp[2][0] = 1; 张数为2,可得 2 - 2*2 <0;直接取0; 即1种解法,即0+1+0=1 | 讨论1: 张数为0 dp[1][3] ]= dp[2][3] = 0; 张数为1,可得 3 - 2 =1; 可得: dp[1][3] = dp[2][1] = 0; 张数为2。 可得3 - 2*2 < 0取值0; 张数为3. 即3-3*2<0,直接取0 0+0+0+0=0,最终取值0
| 张数为0, dp[1][4] = dp[2][4] = 0; 张数为1,可得 4 - 2 =2; dp[1][4] = dp[2][2] = 0; 张数为2. 可得4 - 2*2 = 0. dp[1][4] = dp[2][0] = 1; 张数为3: 4-3*2 < 0;直接取0 张数为4,4-4*2 < 0;直接取0 0+0+1+0+0=1 最终可得1种解法。 |
| index 2 | 1 | 0 | 0 | 0 | 0 |
1. 任何一行的每一列,当张数为0的时候,都是直接依赖下一行的当前列的值。也就是说这个值一定是依赖下一行的当前列的值。
2. col是aim的值,当 zhangshu * arr[row] <= col 的时候,我们是依赖 dp[row + 1][col - (zhangshu * arr[row])]的值的。这一点是非常非常重要的。由此我们可以推导出;
0张,我们依赖y1处的值
1张,依赖y2处的值。
2张,依赖y3处的值
3张,依赖y4处的值
4张,依赖y5处的值
5张,依赖y6处的值
那 x 不就是 y1 + y2 + y3 + y4 + y5 + y6 吗?
x1 不就是 y2 + y3 + y4 + y5 +y6 吗?
状态转移可得。 x = x1 + y1.

根据以上推导,我们是不是可以直接转化成完整的表格,即
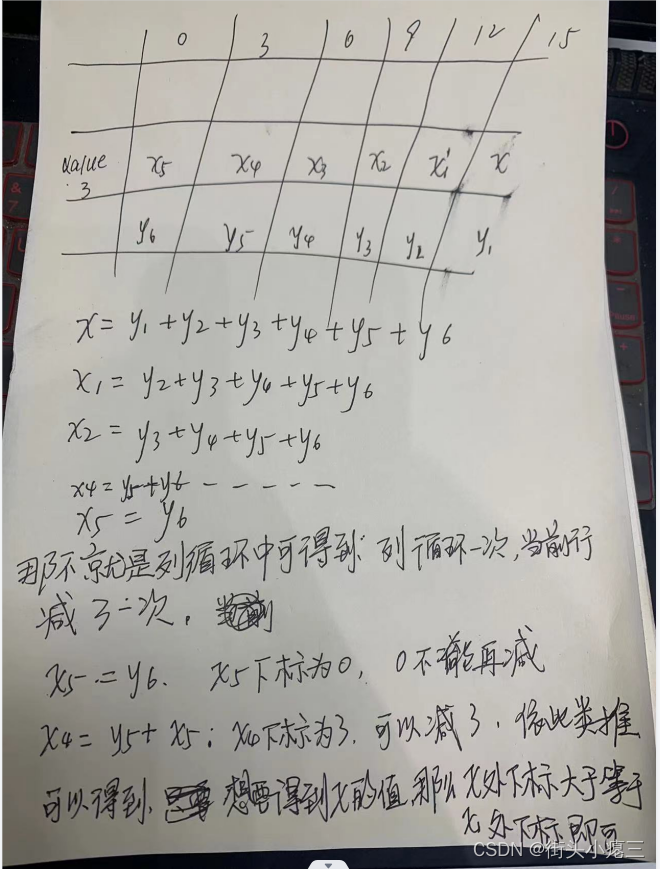
既然我们知道
x = x1 + y1; 假设x处的列下标col为15. 那么x1处的小标不就是 col - value. 此处的value不就是一维数组中的arr[index]的值,即为3。 那么x1处的下标不就是 15 - 3 = 12吗?
for (int zhangshu = 0; zhangshu * arr[row] <= col; zhangshu++);循环是每次枚举下一行的值的。既然下一行的值已经存储在 x1 x2 x3 .......处,那我们还要这个for循环干嘛呢?
时间复杂度优化代码如下:
//动态规划 针对时间复杂度的优化版public static int ways3(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}//老样子int N = arr.length;int[][] dp = new int[N + 1][aim + 1];//最后一行的第一列为1,其余都为0。 根据递归 return aim == 0 ? 1 : 0;得到dp[N][0] = 1;//双层for循环,动态规划的老套路。一维数组arr作为横坐标,aim作为纵坐标for (int row = N -1 ; row >= 0; row--) { //row代表递归中的 indexfor (int col = 0; col <= aim; col++) { //col代表递归中的 aim// 每一列都存在aim为0张的情况,// 下一行的当前列dp[row][col] = dp[row + 1][col];//当前下标col, 那么前一处的下标不就是 col - arr[row] 吗 ?if (col - arr[row] >= 0) {/*** for循环中的 下一行的 dp[row + 1][col - (zhangshu * arr[row])]列** 直接转化为当前行的 前 col - arr[row] 列。*/dp[row][col] += dp[row][col - arr[row]];}}}return dp[0][aim];}以上代码已经对时间复杂度进行了优化,下面按照空间压缩的思维,对空间复杂度再进行优化。
在算法28 算法28:力扣64题,最小路径和------------样本模型-CSDN博客 和 算法29 算法29:不同路径问题(力扣62和63题)--针对算法28进行扩展-CSDN博客中,我已经详细的分析过空间压缩的技巧以及思维。下面直接上代码
空间压缩代码
//动态规划 针对空间复杂度的优化版public static int ways4(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}//老样子int N = arr.length;int[] dp = new int[aim + 1];//最后一行的第一列为1,其余都为0。 根据递归 return aim == 0 ? 1 : 0;得到dp[0] = 1;//双层for循环,动态规划的老套路。一维数组arr作为横坐标,aim作为纵坐标for (int row = N -1 ; row >= 0; row--) { //row代表递归中的 indexfor (int col = 0; col <= aim; col++) { //col代表递归中的 aimif (col - arr[row] >= 0) {dp[col] += dp[col - arr[row]];}}}return dp[aim];}从递归到动态规划,再对动态规划代码进行时间复杂度和空间复杂度进行双重优化。本文重点介绍了从左往右模型的技巧、动态规划的推理、时间复杂度的优化。至于空间复杂度,由于前面2篇博客已经重点分析了,所有没有过多累赘叙述。
从左往右模型总结:
1、 针对固定集合,值不同,就是讨论要和不要的累加和。
2. 针对非固定集合,面值固定,张数无限。口诀就是讨论要与不要,要的话逐步讨论要几张的累加和
下面贴出完整代码,并加入对数器进行海量数据测试:
package code03.动态规划_07.lesson4;/*** arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。* 每个值都认为是一种面值,且认为张数是无限的。* 返回组成aim的方法数* 例如:arr = {1,2},aim = 4* 方法如下:1+1+1+1、1+1+2、2+2* 一共就3种方法,所以返回3*/
public class ContainWaysNotLimitPaper_05 {//递归版本public static int ways(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}return process(arr, 0, aim);}public static int process (int[] arr, int index, int aim){if (index == arr.length) { // 没钱了return aim == 0 ? 1 : 0;}//讨论不同货币组成aim的可能int ways = 0;//因为货币张数无限,所有需要讨论每一种情况。此次,就不是简单的要与不要的问题了for (int zhangshu = 0; zhangshu * arr[index] <= aim; zhangshu++) {/*** 此处,还是讨论要与不要的问题。* 0张代表不要* 要的话需要讨论要几张 :* 要1 张, 那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 要2 张,那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 依次类推*/ways += process(arr, index + 1, aim - zhangshu * arr[index]);}return ways;}//动态规划public static int ways2(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}//老样子int N = arr.length;int[][] dp = new int[N + 1][aim + 1];//最后一行的第一列为1,其余都为0。 根据递归 return aim == 0 ? 1 : 0;得到dp[N][0] = 1;//双层for循环,动态规划的老套路。一维数组arr作为横坐标,aim作为纵坐标for (int row = N -1 ; row >= 0; row--) { //row代表递归中的 indexfor (int col = 0; col <= aim; col++) { //col代表递归中的 aim//此处是比较复杂的,完全套用递归内部的代码。这一层的for循环就是对//要的张数进行讨论。int ways = 0;//此处zhangshu * arr[row] <= col是唯一变化。重点理解for (int zhangshu = 0; zhangshu * arr[row] <= col; zhangshu++) {/*** 此处,还是讨论要与不要的问题。* 0张代表不要* 要的话需要讨论要几张 :* 要1 张, 那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 要2 张,那么后面的数组需要进行递归继续讨论要还是不要,要的话要几张* 依次类推*///根据ways += process(arr, row + 1, aim - zhangshu * arr[row]);推导//此处的aim - zhangshu * arr[index] 需要变成 col - zhangshu * arr[index]ways += dp[row + 1][col - (zhangshu * arr[row])];}dp[row][col] = ways;}}return dp[0][aim];}//动态规划 针对时间复杂度的优化版public static int ways3(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}//老样子int N = arr.length;int[][] dp = new int[N + 1][aim + 1];//最后一行的第一列为1,其余都为0。 根据递归 return aim == 0 ? 1 : 0;得到dp[N][0] = 1;//双层for循环,动态规划的老套路。一维数组arr作为横坐标,aim作为纵坐标for (int row = N -1 ; row >= 0; row--) { //row代表递归中的 indexfor (int col = 0; col <= aim; col++) { //col代表递归中的 aim// 每一列都存在aim为0张的情况,// 下一行的当前列dp[row][col] = dp[row + 1][col];//当前下标col, 那么前一处的下标不就是 col - arr[row] 吗 ?if (col - arr[row] >= 0) {/*** for循环中的 下一行的 dp[row + 1][col - (zhangshu * arr[row])]列** 直接转化为当前行的 前 col - arr[row] 列。*/dp[row][col] += dp[row][col - arr[row]];}}}return dp[0][aim];}//动态规划 针对空间复杂度的优化版public static int ways4(int[] arr, int aim) {if (arr == null || arr.length == 0 || aim < 0) {return 0;}//老样子int N = arr.length;int[] dp = new int[aim + 1];//最后一行的第一列为1,其余都为0。 根据递归 return aim == 0 ? 1 : 0;得到dp[0] = 1;//双层for循环,动态规划的老套路。一维数组arr作为横坐标,aim作为纵坐标for (int row = N -1 ; row >= 0; row--) { //row代表递归中的 indexfor (int col = 0; col <= aim; col++) { //col代表递归中的 aimif (col - arr[row] >= 0) {dp[col] += dp[col - arr[row]];}}}return dp[aim];}// 为了测试public static int[] randomArray(int maxLen, int maxValue) {int N = (int) (Math.random() * maxLen);int[] arr = new int[N];boolean[] has = new boolean[maxValue + 1];for (int i = 0; i < N; i++) {do {arr[i] = (int) (Math.random() * maxValue) + 1;} while (has[arr[i]]);has[arr[i]] = true;}return arr;}// 为了测试public static void printArray(int[] arr) {for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}public static void main(String[] args) {/* int[] arr = {1,2,3};int aim = 13;System.out.println(ways(arr, aim));System.out.println(ways2(arr, aim));System.out.println(ways3(arr, aim));System.out.println(ways4(arr, aim));*/// 为了测试int maxLen = 10;int maxValue = 30;int testTime = 1000000;System.out.println("测试开始");for (int i = 0; i < testTime; i++) {int[] arr = randomArray(maxLen, maxValue);int aim = (int) (Math.random() * maxValue);int ans1 = ways(arr, aim);int ans2 = ways2(arr, aim);int ans3 = ways3(arr, aim);int ans4 = ways4(arr, aim);if (ans1 != ans2 || ans1 != ans3 || ans1 != ans4) {System.out.println("Oops!");printArray(arr);System.out.println(aim);System.out.println(ans1);System.out.println(ans2);System.out.println(ans3);break;}}System.out.println("测试结束");}
}