Geometry
- π \pi π: arccos ( − 1 ) \arccos(-1) arccos(−1)
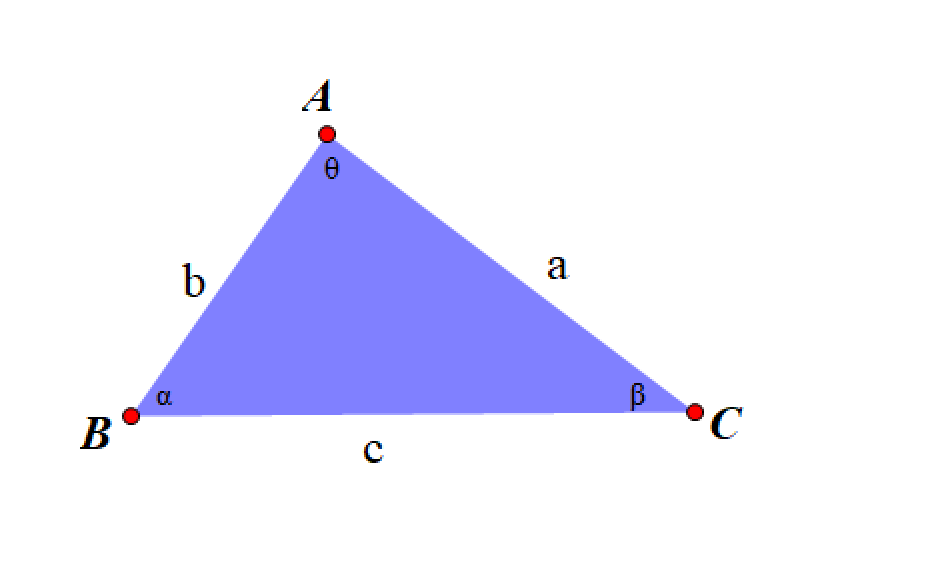
- 余弦定理:对于任意三角形(三边长为 a , b , c a,b,c a,b,c),则有 c 2 = a 2 + b 2 − 2 a b cos θ c^2=a^2+b^2-2ab\cos_{\theta} c2=a2+b2−2abcosθ,其中 θ \theta θ 为 a , b a,b a,b 边的夹角。
- 正弦定理: a sin α = b sin β = c sin θ \frac{a}{\sin_{\alpha}}=\frac{b}{\sin_{\beta}}=\frac{c}{\sin_{\theta}} sinαa=sinβb=sinθc
- 向量的加法: A ⃗ + B ⃗ = C ⃗ \vec A+\vec B = \vec C A+B=C

-
向量的减法: A ⃗ − B ⃗ = C ⃗ \vec A-\vec B=\vec C A−B=C(按照加法的定义并通过平移旋转即可得到)

-
内积(点积): A ⃗ ⋅ B ⃗ = ∣ A ⃗ ∣ ∣ B ⃗ ∣ cos θ \vec A\cdot \vec B=|\vec A||\vec B|\cos_{\theta} A⋅B=∣A∣∣B∣cosθ
几何意义:向量 A ⃗ \vec A A 在向量 B ⃗ \vec B B 上的投影与 B ⃗ \vec B B 的长度的乘积
Code:(证明略)
double dot (Point A, Point B) { return A.x * B.x + A.y * B.y } -
外积(叉积): A ⃗ × B ⃗ = ∣ A ⃗ ∣ ∣ B ⃗ ∣ sin θ \vec A\times \vec B=|\vec A||\vec B|\sin_{\theta} A×B=∣A∣∣B∣sinθ
几何意义:向量 A ⃗ \vec A A 与向量 B ⃗ \vec B B 组成的平行四边形的面积( B ⃗ \vec B B 在 A ⃗ \vec A A 的逆时针方向为正)
Code:(证明略)
double cross(Point A, Point B) { return A.x * B.y - B.x * A.y }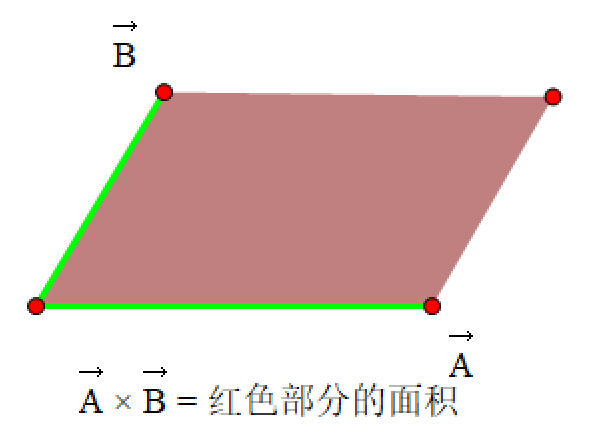
-
向量取模(向量的长度)
向量的长度为 d o t a ⃗ , a ⃗ \sqrt{\mathrm{dot_{\vec a,\vec a}}} dota,a,即 x 2 + y 2 \sqrt{x^2+y^2} x2+y2
注意:前面包括后面的所有向量都默认起点为平面直角坐标系原点
Code:
double Length(Point A) { return sqrt(dot(a, a)); } -
计算向量夹角
已知向量的点积为 ∣ A ⃗ ∣ ∣ B ⃗ ∣ cos θ |\vec A||\vec B|\cos_{\theta} ∣A∣∣B∣cosθ,现在要求 θ \theta θ,就是 KaTeX parse error: Undefined control sequence: \acos at position 1: \̲a̲c̲o̲s̲_\frac{\vec A \…
Code:
double Angle(Point A, Point B) { return acos(dot(A, B)) / Length(A) / Length(B)} -
向量 A ⃗ \vec A A 顺时针旋转 θ \theta θ 角度
( x , y ) [ cos θ − sin θ sin θ cos θ ] (x,y) \begin{bmatrix} \cos_{\theta} &-\sin_{\theta}\\ \sin_{\theta} &\cos_{\theta} \end{bmatrix} (x,y)[cosθsinθ−sinθcosθ]
其中 ( x , y ) (x,y) (x,y) 表示向量 A ⃗ \vec A A,证明略。
Code:
Point Rotate(Point A, int Theta) {return Point(A.x * cos(Theta) + A.y * sin(Theta), -A.x * sin(Theta) + A.y * cos(Theta)) } -
直线点向式表示方式: P + t V ⃗ P+t\vec V P+tV
-
判断点在直线上: A ⃗ × B ⃗ = 0 \vec A \times \vec B=0 A×B=0, B ⃗ \vec B B 是表示该直线的向量, A ⃗ \vec A A 是该点与 B ⃗ \vec B B 的起点所组成的向量
-
判断 2 2 2 条直线的位置关系,交点的位置(如果有)
cross(v, w) = 0,则两直线平行或重合。两条直线: P + t V ⃗ P+t\vec V P+tV, Q + t W ⃗ Q+t\vec W Q+tW
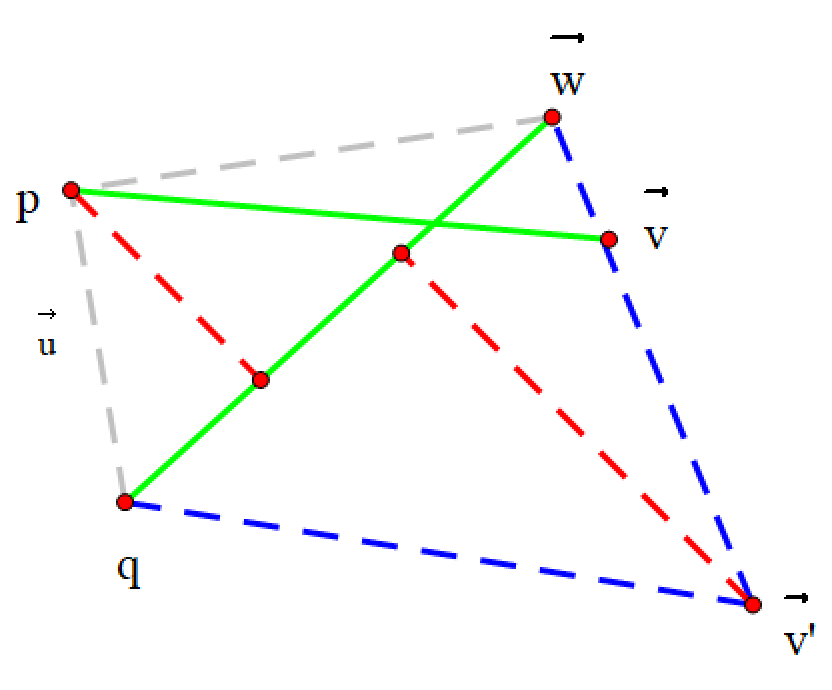
V ⃗ ′ \vec V ' V′ 为 V ⃗ \vec V V 的平移,红线为两个三角形的高,此时必有 2 2 2 个三角形相似
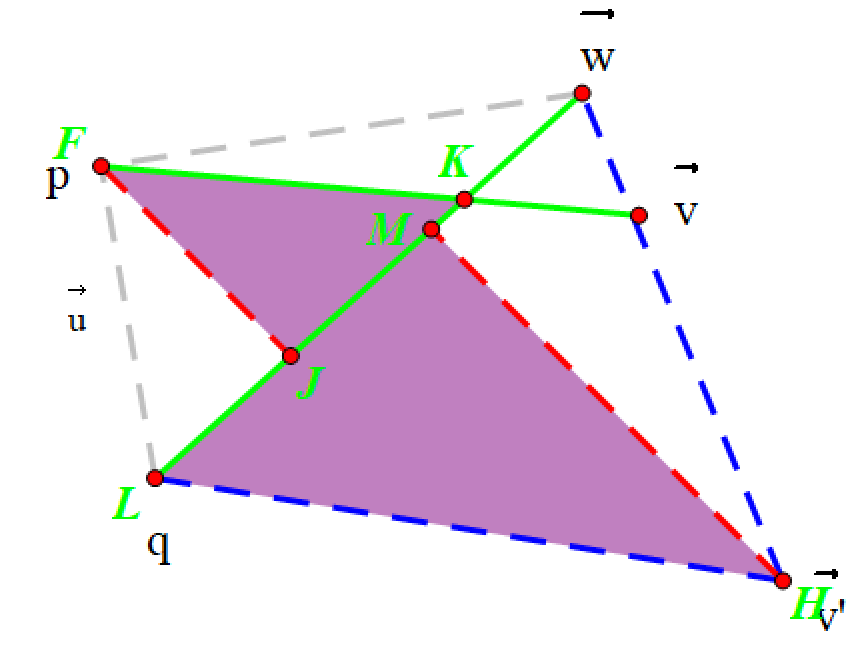
即, 2 2 2 个紫色三角形是相似的,因为 V ⃗ ′ \vec V' V′ 是 V ⃗ \vec V V 的平移,所以内错角相等,即 KaTeX parse error: Undefined control sequence: \ang at position 1: \̲a̲n̲g̲ ̲FMJ=\ang HLM,且都是直角三角形,所以相似。那么, F J M H = F K L H \frac{FJ}{MH}=\frac{FK}{LH} MHFJ=LHFK,因为 L H = ∣ V ⃗ ∣ LH=|\vec V| LH=∣V∣,所以 F J M H = F K ∣ V ⃗ ∣ \frac{FJ}{MH}=\frac{FK}{|\vec V|} MHFJ=∣V∣FK,而 K K K 的坐标为 P + V ⃗ F K ∣ V ⃗ ∣ P+\vec V \frac{FK}{|\vec V|} P+V∣V∣FK。所以只需要求出 F J M H \frac{FJ}{MH} MHFJ 即可,而 F J M H \frac{FJ}{MH} MHFJ 恰好等于 W ⃗ × u ⃗ V ⃗ × W ⃗ \frac{\vec W\times \vec u}{\vec V\times \vec W} V×WW×u。
故, K K K 点的坐标为 P + V ⃗ W ⃗ × u ⃗ V ⃗ × W ⃗ P+\vec V \frac{\vec W\times \vec u}{\vec V\times \vec W} P+VV×WW×u
Point Line_Intersection(Point P, Vector V, Point Q, Vector W) {Vector u = P - Q;return P + V * cross(W, u) / cross(V, W); } -
点到直线的距离

设向量 V ⃗ \vec V V 为 B − A B-A B−A, W ⃗ \vec W W 为 P − A P-A P−A。
则有, V ⃗ × W ⃗ L e n g t h V ⃗ \frac{\vec V\times \vec W}{\mathrm{Length_{\vec V}}} LengthVV×W 为点 P P P 到 A B AB AB 的距离。
-
点到线段的距离
与 14 14 14 略有不同,边界情况:如果线段为 1 1 1 个点,则就是 P P P 与线段端点所组成的向量的模长。
如果 V 1 ⃗ ⋅ V 2 ⃗ < 0 \vec{V_1}\cdot \vec{V_2}<0 V1⋅V2<0,则为 ∣ V 2 ⃗ ∣ |\vec {V_2}| ∣V2∣。解释: V ⃗ 1 ⋅ V ⃗ 2 \vec V_1 \cdot \vec V_2 V1⋅V2 的符号正负取决于 cos θ \cos_\theta cosθ,当 θ > 90 ° \theta>90\degree θ>90° 时, cos θ < 0 \cos_\theta<0 cosθ<0,恰好是到线段左端点的距离为点 P P P 到线段的距离。

如果 V ⃗ 3 ⋅ V ⃗ 1 > 0 \vec V_3\cdot \vec V_1>0 V3⋅V1>0,则为 ∣ V ⃗ 3 ∣ |\vec V_3| ∣V3∣,证明类似。
反之,则为点到直线的距离。
-
点在直线上的投影
用点积来求, A + V ⃗ ( d o t V ⃗ , p − a ⃗ d o t V ⃗ , V ⃗ ) A+\vec V (\mathrm{\frac{dot_{\vec V,\vec {p-a}}}{dot_{\vec V,\vec V}}}) A+V(dotV,VdotV,p−a)
与上面类似
-
点 P P P 是否在线段 A B AB AB 上
首先, c r o s s P − A , P − B = 0 \mathrm{cross_{P-A,P-B}}=0 crossP−A,P−B=0,这样保证了 P , A , B P,A,B P,A,B 三点共线。
其次, d o t P − A , P − B ≤ 0 \mathrm{dot_{P-A,P-B}}\le0 dotP−A,P−B≤0,即 cos θ ≤ 0 \cos_{\theta}\le0 cosθ≤0,当 P P P 在线段上, 2 2 2 个向量相向, θ \theta θ 为 180 ° 180\degree 180°, cos \cos cos 为负。
-
判断 2 2 2 条 线段 是否相交
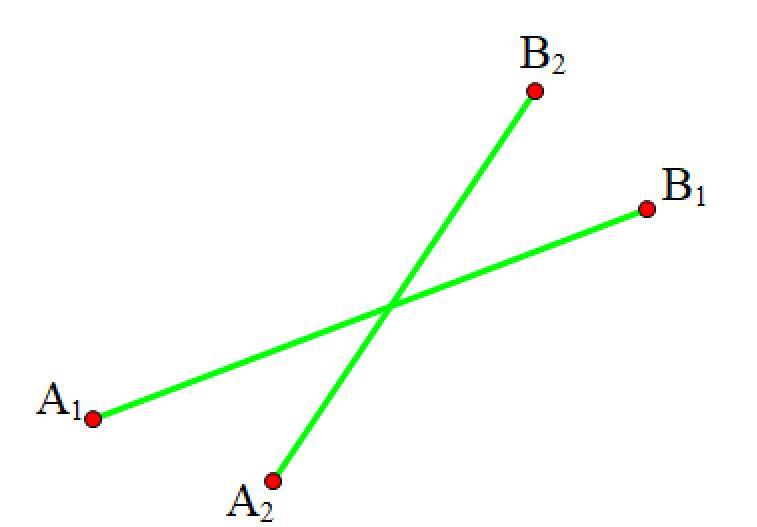
即判断 A 2 , B 2 A_2,B_2 A2,B2 是否在 A 1 B 1 A_1B_1 A1B1 的 2 2 2 侧,且 A 1 , B 1 A_1,B_1 A1,B1 在 A 2 , B 2 A_2,B_2 A2,B2 的 2 2 2 侧。
用叉积做即可。