【十六】【动态规划】97. 交错字符串、712. 两个字符串的最小ASCII删除和、718. 最长重复子数组，三道题目深度解析

动态规划

动态规划就像是解决问题的一种策略，它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题，并将每个小问题的解保存起来。这样，当我们需要解决原始问题的时候，我们就可以直接利用已经计算好的小问题的解，而不需要重复计算。

动态规划与数学归纳法思想上十分相似。

数学归纳法：

  1. 基础步骤（base case）：首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况，可以直接验证命题是否成立。

  2. 归纳步骤（inductive step）：假设命题在某个情况下成立，然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。

通过反复迭代归纳步骤，我们可以推导出命题在所有情况下成立的结论。

动态规划：

  1. 状态表示：

  2. 状态转移方程：

  3. 初始化：

  4. 填表顺序：

  5. 返回值：

数学归纳法的基础步骤相当于动态规划中初始化步骤。

数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。

动态规划的思想和数学归纳法思想类似。

在动态规划中，首先得到状态在最小的基础情况下的值，然后通过状态转移方程，得到下一个状态的值，反复迭代，最终得到我们期望的状态下的值。

接下来我们通过三道例题，深入理解动态规划思想，以及实现动态规划的具体步骤。

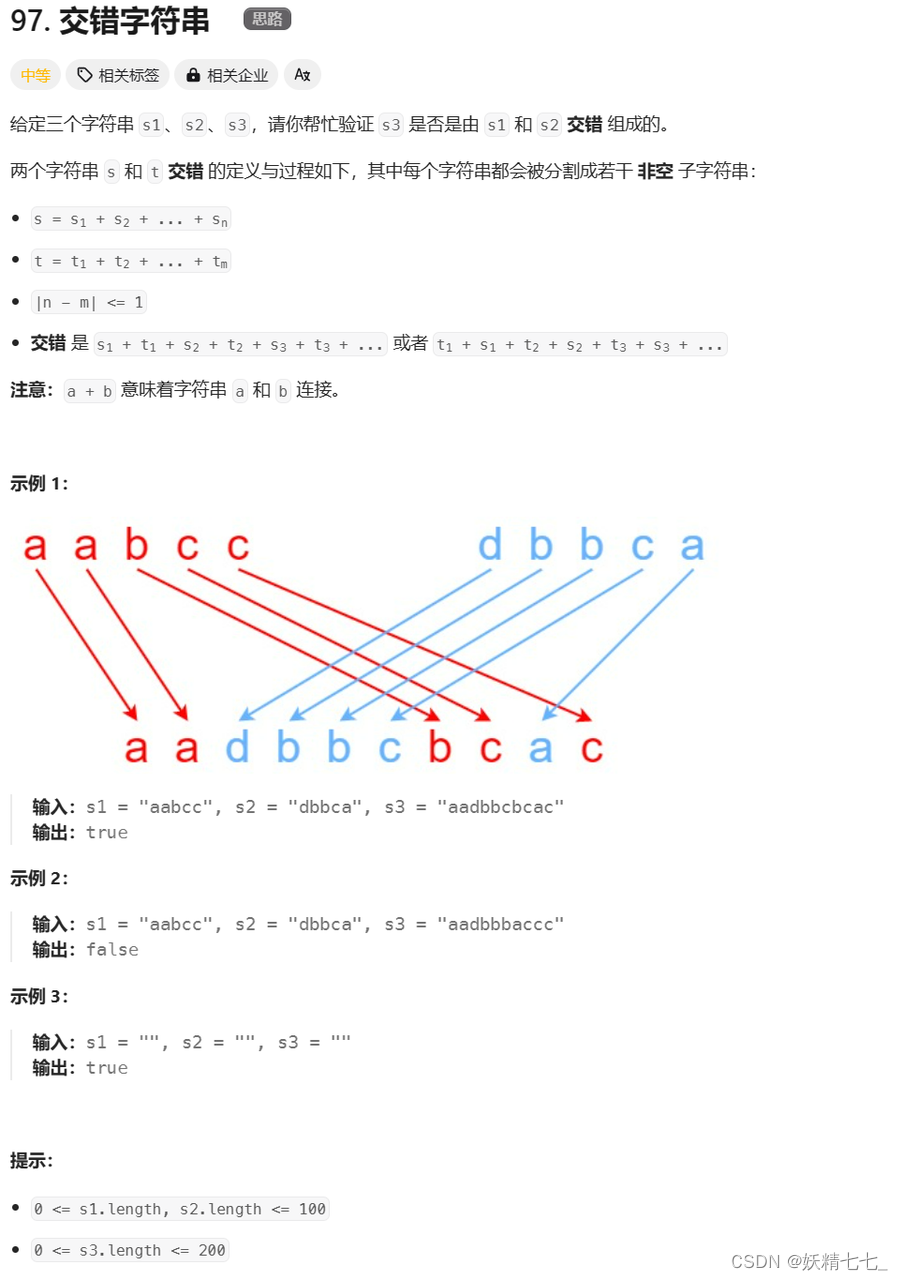
97. 交错字符串 - 力扣（LeetCode）

题目解析

状态表示

对于两个字符串之间的dp问题，我们的一般的思考方式如下：

  1. 选取第一个字符串的[0,i]区间以及第二个字符串的[0,j]区间当成研究对象，结合题目要求来定义状态表示。

  2. 然后根据两个区间上最后一个位置的状况进行分类讨论，从而确定状态转移方程。

由于这段题目里面空串是研究意义的，因此我们先预处理一下原字符串，前面统一加上一个占位符：s1=s1+“ ”，s2=s2+” “，s3=s3+” “；

根据上述思路，我们很容易可以定义这样一个状态表示，

定义dp[i][j]表示字符串s1中[1,i]区间内的字符串以及s2中[1,j]区间内的字符串能否拼接成s3中[1,i+j]区间内的字符串。

状态转移方程

  1. 如果s3[i+j]==s1[i]， 此时s3[i+j]与s1[i]匹配，如果s1[1,i-1]和s2[1,j]可以拼成s3[1,i+j-1]说明s1[1,i]和s2[1,j]可以拼成s3[1,i+j]，此时dp[i][j]=dp[i-1][j]；

  2. 如果s3[i+j]==s2[j], 此时s3[i+j]与s2[i]匹配，如果s1[1,i]和s2[1,j-1]可以拼成s3[1,i+j-1]说明s1[1,i]和s2[1,j]可以拼成s3[1,i+j]，此时dp[i][j]=dp[i][j-1]；

  3. 如果s3[i+j]！=s1[i]&&s3[i+j]!=s2[j]， 此时dp[i][j]=false；

综上所述，将false设置为初始值，得到状态转移方程为

 

    dp[i][j] = (s1[i] == s3[i + j] && dp[i - 1][j]) ||(s2[j] == s3[i + j] && dp[i][j - 1]);
 

初始化
 

 

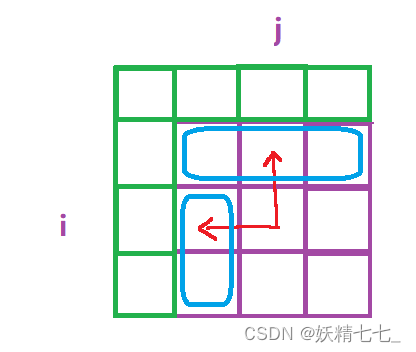
根据状态转移方程，我们知道，想要推到（i，j）位置的状态，我们需要用到（i-1，j）（i，j-1）位置的状态。
 

所以我们需要初始化第一行和第一列。
 

  1.  
    初始化第一行， 第一行表示s1是空串，此时s2[1,j]必须和s3[1,i+j]对应相等，dp[i][j]才为true。
     
  2.  
    初始化第一列， 第一列表示s2是空串，此时s1[1,j]必须和s3[1,i+j]对应相等，dp[i]j]才为true。
     
 

 

故初始化为，
 

 

    for (int j = 1; j <= n; j++) if (s2[j] == s3[j])dp[0][j] = true;elsebreak;for (int i = 1; i <= m; i++)if (s1[i] == s3[i])dp[i][0] = true;elsebreak;
 

填表顺序
 

根据状态转移方程，我们知道，想要推到（i，j）位置的状态，我们需要用到（i-1，j）（i，j-1）位置的状态。
 

  1.  
    固定i，改变j， i的变化需要从小到大，由于需要用到（i，j-1）位置的状态，所以j的变化也需要从小到大。
     
  2.  
    固定j，改变i， j的变化需要从小到大，由于需要用到（i-1，j）位置的状态，所以i的变化也需要从小到大。
     
 

返回值
 

定义dp[i][j]表示字符串s1中[1,i]区间内的字符串以及s2中[1,j]区间内的字符串能否拼接成s3中[1,i+j]区间内的字符串。
 

结合题目意思，我们需要判断字符串s1中[1,m]区间内的字符串以及s2中[1,n]区间内的字符串能否拼接成s3中[1,m+n]区间内的字符串。
 

故返回dp[m][n]；
 

代码实现
 

 

class Solution {
public:bool isInterleave(string s1, string s2, string s3) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int m = s1.size(), n = s2.size();if (m + n != s3.size())return false;s1 = " " + s1, s2 = " " + s2, s3 = " " + s3;vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));dp[0][0] = true;for (int j = 1; j <= n; j++) if (s2[j] == s3[j])dp[0][j] = true;elsebreak;for (int i = 1; i <= m; i++)if (s1[i] == s3[i])dp[i][0] = true;elsebreak;for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)dp[i][j] = (s1[i] == s3[i + j] && dp[i - 1][j]) ||(s2[j] == s3[i + j] && dp[i][j - 1]);return dp[m][n];}
};
 

712. 两个字符串的最小ASCII删除和 - 力扣（LeetCode）
 

 

题目解析
 

 

状态表示
 

对于两个字符串之间的dp问题，我们的一般的思考方式如下：
 

  1.  
    选取第一个字符串的[0,i]区间以及第二个字符串的[0,j]区间当成研究对象，结合题目要求来定义状态表示。
     
  2.  
    然后根据两个区间上最后一个位置的状况进行分类讨论，从而确定状态转移方程。
     
 

根据上述思路，我们很容易可以定义这样一个状态表示，
 

定义dp[i][j]表示s1[0,i]和s2[0,j]区间中所有公共子序列ASCII的最大和。
 

状态转移方程
 

 

  1.  
    如果公共子序列包括s1[i]和s2[j]，此时s1[i]==s2[j]， 此时dp[i][j]=dp[i-1][j-1]+s1[i]；或者dp[i][j]=dp[i-1][j-1]+s2[j]；
     
  2.  
    如果公共子序列包括s1[i]但是不包括s2[j]， 因为要使得公共子序列ASCII尽可能大，所以此时s1[i]!=s2[j], 此时dp[i][j]=dp[i][j-1];
     
  3.  
    如果公共子序列包括s2[j]但是不包括s1[i]， 因为要使得公共子序列ASCII尽可能大，所以此时s1[i]!=s2[j], 此时dp[i][j]=dp[i-1][j];
     
  4.  
    如果公共子序列不包括s1[i]也不包括s2[j]， 因为要使得公共子序列ASCII尽可能大，所以此时s1[i]!=s2[j], 此时dp[i][j]=dp[i-1][j-1];
     
 

 

将上述情况进行合并和简化，得到状态转移方程，
 

 

    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);if (s1[i] == s2[j])dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i]);

 

初始化
 

 

根据状态转移方程，我们知道在推导（i，j）位置的状态时需要用到（i，j-1）（i-1，j）（i-1，j-1）以及s1（i-1）和s2（j-1）的值。
 

所以蓝色部分会发生越界情况，此时推导这些位置的状态没有前驱值，所以我们需要将这些位置的状态进行初始化。
 

 

我们可以正常对这些位置进行初始化，也可以添加虚拟结点代替这些位置的虚拟化。
 

添加虚拟节点，即多添加一行和一列，代替原先需要初始化的位置，现在只需要初始化绿色位置的值，即可。这样做的好处是绿色位置的初始化过程可能很简单，而蓝色位置的初始化过程可能稍微复杂。
 

 

我们添加虚拟节点后，状态表示、状态转移方程会发生改变，即 定义dp[i][j]表示s1[0,i-1]和s2[0,j-1]区间中所有公共子序列ASCII的最大和。
 

 

    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);if (s1[i - 1] == s2[j - 1])dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i - 1]);
 

 

添加虚拟结点之后有两点注意事项，
 

  1.  
    初始化虚拟节点，必须保证推导后续位置的状态的正确性。
     
  2.  
    下标的映射关系。
     
 

 

初始化虚拟节点：
 

我们根据状态表示，定义dp[i][j]表示s1[0,i-1]和s2[0,j-1]区间中所有公共子序列ASCII的最大和，可以将第一行和第一列虚拟节点位置表示为空串的意义，统一状态表示。
 

接下来初始化绿色位置的状态。
 

  1.  
    初始化第一行， 此时i=0，表示s1为空串，公共子序列不存在，所以对应ASCII值应该为0。将第一行全部初始化为0。
     
  2.  
    初始化第一列， 此时j=0，表示s2为空串，公共子序列不存在，所以对应ASCII值应该为0。将第一列全部初始化为0。
     
 

下标映射关系：
 

  1.  
    此时，定义dp[i][j]表示s1[0,i-1]和s2[0,j-1]区间中所有公共子序列ASCII的最大和。 dp中i对应s1的i-1位置，dp中j对应s2的j-1位置。
     
  2.  
    如果在s1，s2前面添加一个占位符，就可以使得dp中i，j继续映射s1，s2中i，j。
     
 

 

我们这里选择第一种解决办法。
 

填表顺序
 

根据状态转移方程，
 

 

    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);if (s1[i - 1] == s2[j - 1])dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i - 1]);
 

我们知道在推导（i，j）位置的状态时，需要用到（i，j-1）（i-1，j）（i-1，j-1）以及s1（i-1）和s2（j-1）的值。
 

  1.  
    固定i改变j， i的变化需要从小到大，由于需要用到（i，j-1）位置的状态，所以j的变化需要从小到大。
     
  2.  
    固定j改变i， j的变化需要从小到大，由于需要用到（i-1，j）位置的状态，所以j的变化需要从小到大。
     
 

返回值
 

根据状态表示，定义dp[i][j]表示s1[0,i-1]和s2[0,j-1]区间中所有公共子序列ASCII的最大和。
 

结合题目要求，我们需要找到s1[0,m-1]和s2[0,n-1]区间中所有公共子序列ASCII的最大和。然后返回”s1，s2中ASCII和“ - 2*dp[m][n]；
 

代码实现
 

 

class Solution {
public:int minimumDeleteSum(string s1, string s2) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int m = s1.size(), n = s2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++) {dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);if (s1[i - 1] == s2[j - 1])dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i - 1]);}int sum = 0; // 统计元素和for (auto s : s1)sum += s;for (auto s : s2)sum += s;return sum - dp[m][n] - dp[m][n];}
};
 

718. 最长重复子数组 - 力扣（LeetCode）
 

 

题目解析
 

 

状态表示
 

对于两个字符串之间的dp问题，我们的一般的思考方式如下：
 

  1.  
    选取第一个字符串的[0,i]区间以及第二个字符串的[0,j]区间当成研究对象，结合题目要求来定义状态表示。
     
  2.  
    然后根据两个区间上最后一个位置的状况进行分类讨论，从而确定状态转移方程。
     
 

根据上述思路，我们很容易可以定义这样一个状态表示，
 

dp[i][j]表示以nums1中i位置元素结尾、nums2中j位置元素结尾的所有公共子数组中，最长的公共子数组长度值。
 

状态转移方程
 

 

  1.  
    如果nums1[i]==nums2[j]， 因为是子数组，所以，如果以nums1[i]、nums2[j]为结尾的公共子数组长度大于等于2，此时一定包括nums1[i-1]、nums[j-1]元素。此时dp[i][j]=dp[i-1][j-1]+1。
     
  2.  
    如果nums1[i]==nums2[j]， 此时不存在以nums1[i]、nums2[j]为结尾的公共子数组，所以长度为0。
     
 

 

故状态转移方程为，
 

 

if (nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1, ret = max(ret, dp[i][j]);

 

初始化
 

 

根据状态转移方程，我们知道在推导（i，j）位置的状态时可能需要用到（i-1，j-1）位置的状态。
 

所以蓝色位置的状态会发生越界，此时推导（i，j）位置的状态时没有前驱值，所以我们需要初始化这些位置的状态。
 

或者我们可以添加虚拟节点，即多添加一行和一列，使这些虚拟节点成为蓝色位置的前驱，这样就不用初始化蓝色位置的值，而变为初始化虚拟节点即可。
 

这样做的好处是，虚拟结点的初始化可能比蓝色部分位置状态的初始化要简便许多。
 

 

 

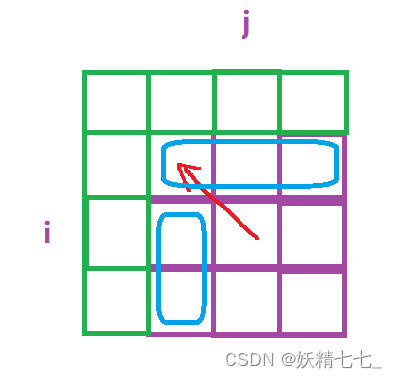
添加虚拟结点后，状态表示和状态转移方程会发生改变，即，
 

dp[i][j]表示以nums1中i-1位置元素结尾、nums2中j-1位置元素结尾的所有公共子数组中，最长的公共子数组长度值。
 

 

if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1, ret = max(ret, dp[i][j]);
 

 

添加虚拟节点后，有两点注意事项，
 

  1.  
    初始化虚拟节点，必须保证推导后续位置的状态的正确性。
     
  2.  
    下标的映射关系。
     
 

 

初始化虚拟节点：
 

我们根据状态表示，dp[i][j]表示以nums1中i-1位置元素结尾、nums2中j-1位置元素结尾的所有公共子数组中，最长的公共子数组长度值，可以将第一行和第一列虚拟节点位置表示为空串的意义，统一状态表示。
 

接下来初始化绿色位置的状态。
 

  1.  
    初始化第一行， 此时i=0，表示nums1为空串，公共子数组不存在，所以对应长度值应该为0。将第一行全部初始化为0。
     
  2.  
    初始化第一列， 此时j=0，表示nums2为空串，公共子数组不存在，所以对应长度值应该为0。将第一列全部初始化为0。
     
 

下标映射关系：
 

  1.  
    此时，定义dp[i][j]表示nums1[0,i-1]和nums2[0,j-1]区间中所有公共子序列ASCII的最大和。 dp中i对应nums1的i-1位置，dp中j对应nums2的j-1位置。
     
  2.  
    如果在nums1，nums2前面添加一个占位符，就可以使得dp中i，j继续映射nums1，nums2中i，j。
     
 

 

我们这里选择第一种解决办法。
 

填表顺序
 

根据状态转移方程，我们知道在推导（i，j）位置的状态时可能需要用到（i-1，j-1）位置的状态。
 

  1.  
    固定i改变j， 此时i的变化需要从小到大，j的变化可以从小到大也可以从大到小。
     
  2.  
    固定j改变i， 此时j的变化需要从小到大，i的变化可以从小到大也可以从大到小。
     
 

返回值
 

dp[i][j]表示以nums1中i-1位置元素结尾、nums2中j-1位置元素结尾的所有公共子数组中，最长的公共子数组长度值。
 

结合题目意思，我们需要返回所有情况下最长的公共子数组的长度值，所以我们需要遍历dp表找到最大的值然后返回。
 

代码实现
 

 

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(), n = nums2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));int ret = 0;for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1, ret = max(ret, dp[i][j]);return ret;}
};
 

结尾
 

今天我们学习了动态规划的思想，动态规划思想和数学归纳法思想有一些类似，动态规划在模拟数学归纳法的过程，已知一个最简单的基础解，通过得到前项与后项的推导关系，由这个最简单的基础解，我们可以一步一步推导出我们希望得到的那个解，把我们得到的解依次存放在dp数组中，dp数组中对应的状态，就像是数列里面的每一项。最后感谢您阅读我的文章，对于动态规划系列，我会一直更新，如果您觉得内容有帮助，可以点赞加关注，以快速阅读最新文章。
 

 

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。
 

 

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。
 

 

谢谢您的支持，期待与您在下一篇文章中再次相遇！











本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/327507.html


如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！












相关文章










Redis基础学习一








Redis基础学习一




1. Redis 入门 
1.1. Redis 诞生历程 
1.1.1.从一个故事开始 
08 年的时候有一个意大利西西里岛的小伙子&#xff0c;笔名 antirez&#xff08;http://invece.org/&#xff09;&#xff0c;创建了一个访客信息网站 LLOOGG.COM。有的时候我们需要知道网站的访问情况&#xff0c;…




阅读更多...

















软件测试/测试开发丨Vuetify框架的使用








软件测试/测试开发丨Vuetify框架的使用




介绍 
Vuetify 是一个基于 Vue.js 精心打造 UI 组件库&#xff0c;整套 UI 设计为 Material 风格。能够让没有任何设计技能的开发者创造出时尚的 Material 风格界面。 
为什么要使用Vuetify框架 
所有组件遵从 Material Design 设计规范&#xff0c;UI 体验非常优秀&#xff0c…




阅读更多...

















软件测试|深入解析Docker Run命令：创建和启动容器的完全指南








软件测试|深入解析Docker Run命令：创建和启动容器的完全指南




简介 
Docker是一种流行的容器化平台&#xff0c;用于构建、分发和运行应用程序。其中一个最基本且重要的Docker命令是docker run&#xff0c;用于创建和启动容器。本文将详细解析docker run命令的用途、参数和示例&#xff0c;帮助您全面掌握创建和启动容器的过程。 
docker r…




阅读更多...

















Springboot整合MQ学习记录








Springboot整合MQ学习记录




Mq介绍 
RabbitMQ是由erlang语言开发&#xff0c;基于AMQP&#xff08;Advanced Message Queue 高级消息队列协议&#xff09;协议实现的消息队列&#xff0c;它是一种应用程序之间的通信方法&#xff0c;消息队列在分布式系统开发中应用非常广泛。支持Windows、Linux/Unix、MA…




阅读更多...

















论文阅读_InP-Based_Generic_Foundry_Platform_for_Photonic_Integrated_Circuits








论文阅读_InP-Based_Generic_Foundry_Platform_for_Photonic_Integrated_Circuits




InP-Based_Generic_Foundry_Platform_for_Photonic_Integrated_Circuits 
时间&#xff1a;2018年 
作者&#xff1a;Luc M. Augustin, Member, IEEE, Rui Santos, Erik den Haan, Steven Kleijn, Peter J. A. Thijs, Sylwester Latkowski, Senior Member, IEEE, Dan Zhao, Wei…




阅读更多...

















计算机毕业设计 SpringBoot的一站式家装服务管理系统 Javaweb项目 Java实战项目 前后端分离 文档报告 代码讲解 安装调试








计算机毕业设计 SpringBoot的一站式家装服务管理系统 Javaweb项目 Java实战项目 前后端分离 文档报告 代码讲解 安装调试




&#x1f34a;作者&#xff1a;计算机编程-吉哥 &#x1f34a;简介&#xff1a;专业从事JavaWeb程序开发&#xff0c;微信小程序开发&#xff0c;定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事&#xff0c;生活就是快乐的。 &#x1f34a;心愿&#xff1a;点…




阅读更多...

















探讨一下WebINFO 下的一些思考








探讨一下WebINFO 下的一些思考




在平时的开发中&#xff0c;我们经常看到一个/WEB-INF 这个目录&#xff0c;这个是web 容器初始化加载的一个标准路径。官方解释&#xff1a;WEB-INF 是 Java 的 web 应用的安全目录。所谓安全就是客户端无法访问&#xff0c;只有服务端可以访问的目录。也就是说&#xff0c;这…




阅读更多...

















拜佛行善心要诚，否则就是不敬！








拜佛行善心要诚，否则就是不敬！




佛教所主张的“善因有善果&#xff0c;恶因有恶果”&#xff0c;又叫做“善有善报&#xff0c;恶有恶报”。峰民佛学悟语&#xff1a;“善有善报&#xff0c;恶有恶报。不是不报&#xff0c;时辰未到。”这句话表达的是一种因果循环、报应不爽的善恶法则&#xff0c;它告诉我们…




阅读更多...

















Redis 键中冒号的用途是什么？可以使匹配查询更快吗？








Redis 键中冒号的用途是什么？可以使匹配查询更快吗？




Redis 键中冒号的用途是什么在Redis中&#xff0c;冒号&#xff08;:&#xff09;用作键的分隔符&#xff0c;它的主要作用是创建层次结构和命名空间。通过在键中使用冒号&#xff0c;可以将键分为多个部分&#xff0c;从而更好地组织和管理数据。 以下是冒号在Redis键中的用途…




阅读更多...

















uniapp中uview组件库CircleProgress 圆形进度条丰富的使用方法








uniapp中uview组件库CircleProgress 圆形进度条丰富的使用方法




目录 
#内部实现 
#平台差异说明 
#基本使用 
#设置圆环的动画时间 
#API 
#Props 展示操作或任务的当前进度&#xff0c;比如上传文件&#xff0c;是一个圆形的进度环。 
#内部实现 
组件内部通过canvas实现&#xff0c;有更好的性能和通用性。 
#平台差异说明 
AppH5微信小程…




阅读更多...

















计算机毕业设计选题分享-SSM律师事务所业务管理系统01664（赠送源码数据库）JAVA、PHP，node.js，C++、python，大屏数据可视化等








计算机毕业设计选题分享-SSM律师事务所业务管理系统01664（赠送源码数据库）JAVA、PHP，node.js，C++、python，大屏数据可视化等




SSM律师事务所业务管理系统 摘  要 随着科学技术的飞速发展&#xff0c;社会的方方面面、各行各业都在努力与现代的先进技术接轨&#xff0c;通过科技手段来提高自身的优势&#xff0c;律师事务所业务管理系统当然也不能排除在外。律师事务所业务管理系统是以实际运用为开发背景…




阅读更多...

















AWS(三)：如何在AwsManagedAd目录和windowsAD实例之间建立双向信任。








AWS(三)：如何在AwsManagedAd目录和windowsAD实例之间建立双向信任。




前提&#xff1a; 
1.创建好了一个AWS managed AD目录&#xff0c;我的目录域名为:aws.managed.com 
2.创建好了一个windows AD实例并提升了为域控服务器,实例域名为:aws2.com 看过我AWS 一和二的应该都会创建windows实例了&#xff0c;切记不能将其无缝加入到aws managed AD的…




阅读更多...


















推荐文章












最新文章


















Copyright @ 2022~2023