矩形区域不超过K的最大数值和
题目要求


解题思路
来自[宫水三叶]
从题面来看显然是一道[二维前缀和]的题目。本题预处理前缀和的复杂度为O(m* n)
搜索所有子矩阵需要枚举[矩形左上角]和[矩形右下角],复杂度是 O ( m 2 ∗ n 2 ) O(m^2 * n^2) O(m2∗n2),因此,如果把本题当作二维前缀和模板题来做的话,整体复杂度为 O ( m 2 ∗ n 2 ) O(m^2 * n^2) O(m2∗n2).
数据范围是 1 0 2 10^2 102,对应的计算量是 1 0 8 10^8 108,理论上会超时,但当我们枚举[矩形左上角](i,j)的时候,我们只需要搜索位于(i,j)的右下方的点(p,q)作为[矩形右下角],所以其实我们是取不满 m 2 ∗ n 2 m^2 * n^2 m2∗n2的,但是,仍然存在超时风险。
前缀和 & 二分(抽象一维)
我们来细想一下[朴素二维前缀和]解法是如何搜索答案(子矩阵):通过枚举[左上角] & [右下角]来确定某个矩阵
换句话说是通过枚举(i,j)和(p,q)来唯一确定子矩阵的四条边,每个坐标点可以看作确定子矩阵的某条边。
既然要确定的边有四条,我们如何降低复杂呢?
简单的,我们先思考一下同样是枚举的[两数之和]问题
在[两数之和]中可以暴力枚举两个数,也可以只枚举其中一个数,然后使用数据结构(哈希表)来加速找另一个数(这是一个通用的[降低枚举复杂度]思考方向)。
对应到本题,我们可以枚举其中三条边,然后使用数据结构来加速找第四条边。
当我们确定了三条边(红色)之后,形成的子矩阵就单纯取决于第四条边的位置(黄色):
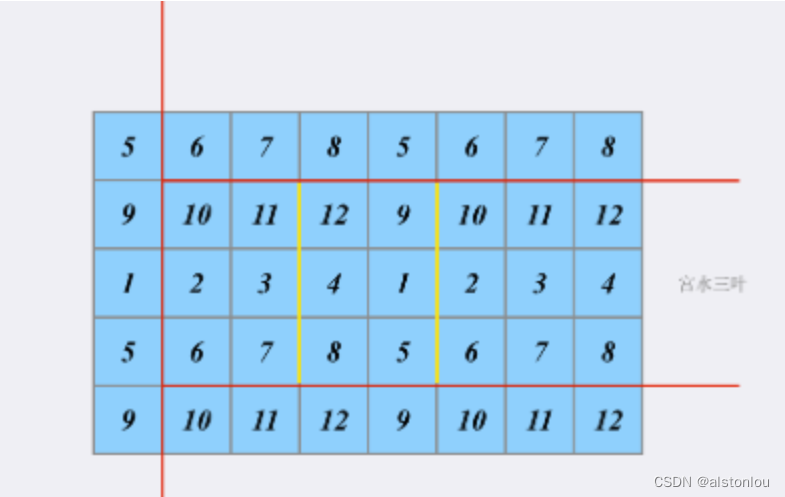
于是问题转换为[如何快速求得第四条边(黄色)的位置在哪]。
我们可以进一步将问题缩小,考虑矩阵之有一行(一维)的情况:
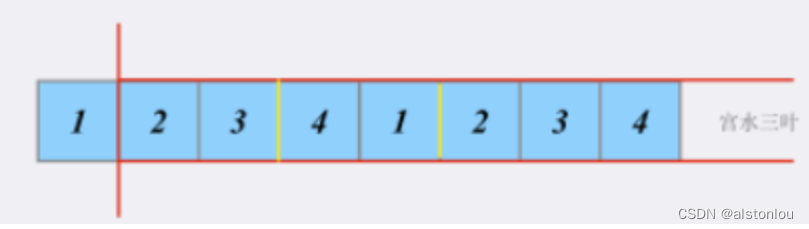
这时候问题进一步转换为[在一维数组中,求解和不超过K的最大连续子数组之和]。
对于这个一维问题,我们可以先预处理出[前缀和],然后枚举子数组的左端点,然后通过[二分]来求解其右端点的位置。
假定我们已经求得一维数组的前缀和数组sum,即可得下标范围[i,j]的和为:
areaSum(i,j) = sum[j] - sum[i-1] <=k
经过变形后得:
sum[j] <= k + sum[i-1]
我们两种思路来最大化areaSum(i,j):
- 确定(枚举)左端点位置
i,求得符合条件的最大右端点sum[j] - 确定(枚举)右端点位置
j,求得符合条件的最小左端点sum[i]
对于没有负权值的一维数组,我们可以枚举左端点i,同时利用前缀和的[单调递增]特性,通过[二分]找到符合sum[j] <= k +sum[i-1]条件的最大值sum[j],从而求解出答案
但是如果是含有负权值的话,前缀和将会丢失[单调递增]的特性,我们也就无法使用枚举i并结合[二分]查找j的做法。
这时候需要将过程反过来处理:我们从左到右枚举j,并使用[有序集合]结构维护遍历过的位置,找到符合sun[j] - k <= sum[i] 条件最小值sum[i],从而求解出答案。
基于上述分析,解决这样的一维数组问题复杂度是 O ( n l o g n ) O(n log n) O(nlogn)。将这样子思路应用到二维需要一点点抽象能力。
同时,将一维思路引用到本题(二维),复杂度要么是 O ( m 2 ∗ n l o g n ) O(m ^2 * n logn) O(m2∗nlogn)要么是 O ( n 2 ∗ m l o g m ) O(n^2 * m log m) O(n2∗mlogm)
我们先不考虑[最大化二分收益]问题,先假设我们是固定枚举[上下行]和[右边列],这时候唯一能够确定一个子矩阵则是取决于[左边列]:
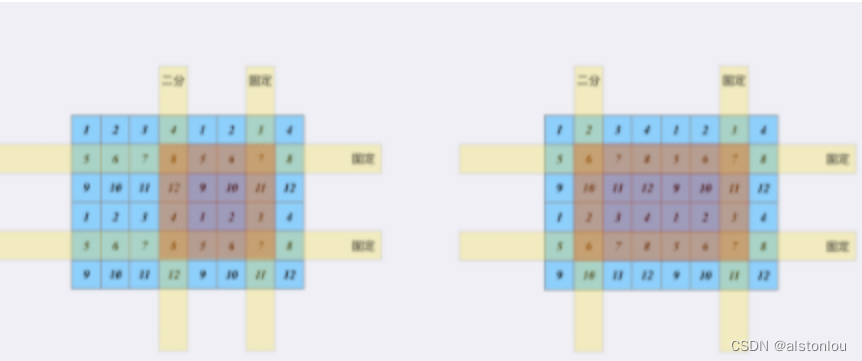
重点是如何与[一维]问题进行关联:显然[目标子矩阵的和]等于[子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵和] - [子矩阵左边列 与 原矩阵左边列 形成的子矩阵和]
我们可以使用area[r]代表[子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵之和],使用area[l-1]代表[子矩阵的左边列 与 原矩阵的左边列 形成的子矩阵和]的话,则有:
target = area[r] - area[l-1] <=k
这与我们[一维问题]完全一直,同时由[上下行]&[右边列]可与直接确定area[r]的大小,通过[有序集合]存储我们遍历r过程中固定所有area[r]从而实现[二分]查找符合area[r] - k <= area[l-1]条件的最小的area[l-1]。
至此,我们通过预处理前缀和+容斥原理彻底将题目转换为[一维问题]进行来求解。
其他解法
首先有三个变量row,col,res第一个记录行,第二个记录列,第三个记录矩形和
然后看二维矩阵matrix,我们有两个索引left,right,这两个索引代表列与列之间的范围。
开始先从第0列开始,同时也作为左边的列left,然后再取右边的列right逐渐将右移。并且记录同一行左边的列与右边的列的和.
这里有个需要注意的,我们首先是取第0列作为左边的列,然后右边的列依次从第0列开始逐渐到最后一列,在此期间同一行的左右列会逐渐相加。当我们这次一整个循环完,左边的列会更新成1,也就是for left in range(col),然后重置新一轮的计算和,再继续循环右边的列。
接下来当我们累加和计算完之后就相当于将二维变成了一维,之后我们将在这个一维里面计算最大的矩形和。一个列表lst用来存放累加的和,一个变量cur用来累加之前算出来的累加列表sums。
我们这里需要找到的是最大的矩形和,但是有一个条件,那就是不大于k。比如我们要求sums(i,j)=sums(0,j)-sums(0,i-1)那么我们可以把sums(i,j)=k且不大于k,sums(0,j)-sums(0,i-1)<=k,可以写成sums(0,j)-k<=sums(0,i-1),我们可以看这个式子是否成立。
所以当我们累加和第一个值之后loc = bisect.bisect_left(lst,cur-k)可以看成sums(0,j)-k<=sums(0,i-1),接下来进行一个if判断,如果成立那么cur-lst[loc]可以看成sums(0,j)-sums(0,i-1)<=k计算出值,之后进行res最大值计算。
想不起来可以参看
https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/solution/javacong-bao-li-kai-shi-you-hua-pei-tu-pei-zhu-shi/
代码
class Solution:def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:import bisectrow = len(matrix)col = len(matrix[0])res = float("-inf")for left in range(col):# 以left为左边界,每行的总和_sum = [0] * rowfor right in range(left, col):for j in range(row):_sum[j] += matrix[j][right]# 在left,right为边界下的矩阵,求不超过K的最大数值和arr = [0]cur = 0for tmp in _sum:cur += tmp# 二分法loc = bisect.bisect_left(arr, cur - k)if loc < len(arr):res = max(cur - arr[loc], res)# 把累加和加入bisect.insort(arr, cur)return res复杂度分析
时间复杂度: O ( m 2 ∗ n 2 ) O(m^2 * n^2 ) O(m2∗n2)
空间复杂度: O ( n ) O(n) O(n)