7-35 有理数均值分数 20-编程知识

7-35 有理数均值分数 20

每日一言

我们把世界看错，反说它欺骗了我们。 --飞鸟集

题目

本题要求编写程序，计算N个有理数的平均值。

输入格式：

输入第一行给出正整数N（≤100）；第二行中按照a1/b1 a2/b2 …的格式给出N个分数形式的有理数，其中分子和分母全是整形范围内的整数；如果是负数，则负号一定出现在最前面。

输出格式：

在一行中按照a/b的格式输出N个有理数的平均值。注意必须是该有理数的最简分数形式，若分母为1，则只输出分子。

输入样例1：

4
1/2 1/6 3/6 -5/10

输出样例1：

1/6

输入样例2：

2
4/3 2/3

输出样例2：

如果不懂化简可以去看
有理分式化简
点一下就可以跳转

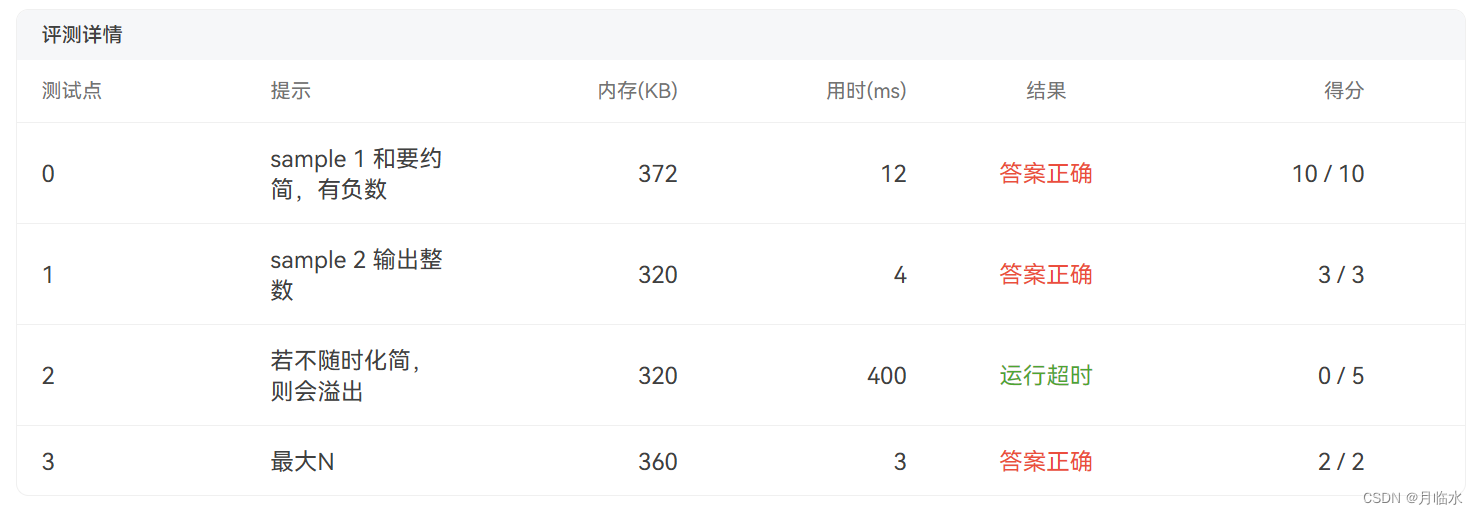
思路一：先计算总结果，最后化简

（运行溢出）
本来想着先计算出总结果，最后再化简的，果然偷懒就拿不了满分 ┭┮﹏┭┮

代码：

#include<stdio.h>
#include<math.h>
int main()
{int n=0;scanf("%d",&n);int i=0;int fz[n];int fm[n];int tmp=0;for(i=0;i<n;i++){scanf("%d/%d",&fz[i],&fm[i]);}int j=0;long long zfm=1;long long zfz=0;for(i=0;i<n;i++){for(j=0;j<n;j++){if(j!=i){fz[i]*=fm[j];}}zfz+=fz[i];zfm*=fm[i];}zfm*=n;for(i=zfm;i>=2;i--){if(zfm%i==0&&zfz%i==0){zfm/=i;zfz/=i;break;}}if(zfz==0){printf("0");return 0;}if(zfm==1)printf("%lld",zfz);elseprintf("%lld/%lld",zfz,zfm);return 0;
}

解释：

用户输入n，表示分数的个数。
定义两个数组fz和fm，用于存储分子和分母。
使用循环，依次读取每个分数的分子和分母并存储到数组中。
初始化两个变量zfz和zfm，分别表示最终的分子和分母，初始值都为0和1。
使用两个嵌套循环，计算每个分数的通分分子，并将通分分子累加到zfz上。
计算所有分数的通分分母，并将其乘以n。
使用循环，从zfm开始递减，判断zfm和zfz是否都能整除以i，如果能整除，则将两者都除以i，即化简为最简形式。
最后，根据zfz和zfm的值的不同情况，进行输出。若zfz为0，则输出0；若zfm为1，则只输出zfz；否则输出zfz和zfm的值。这段代码实现了计算n个分数的和，并化简为最简形式的功能。

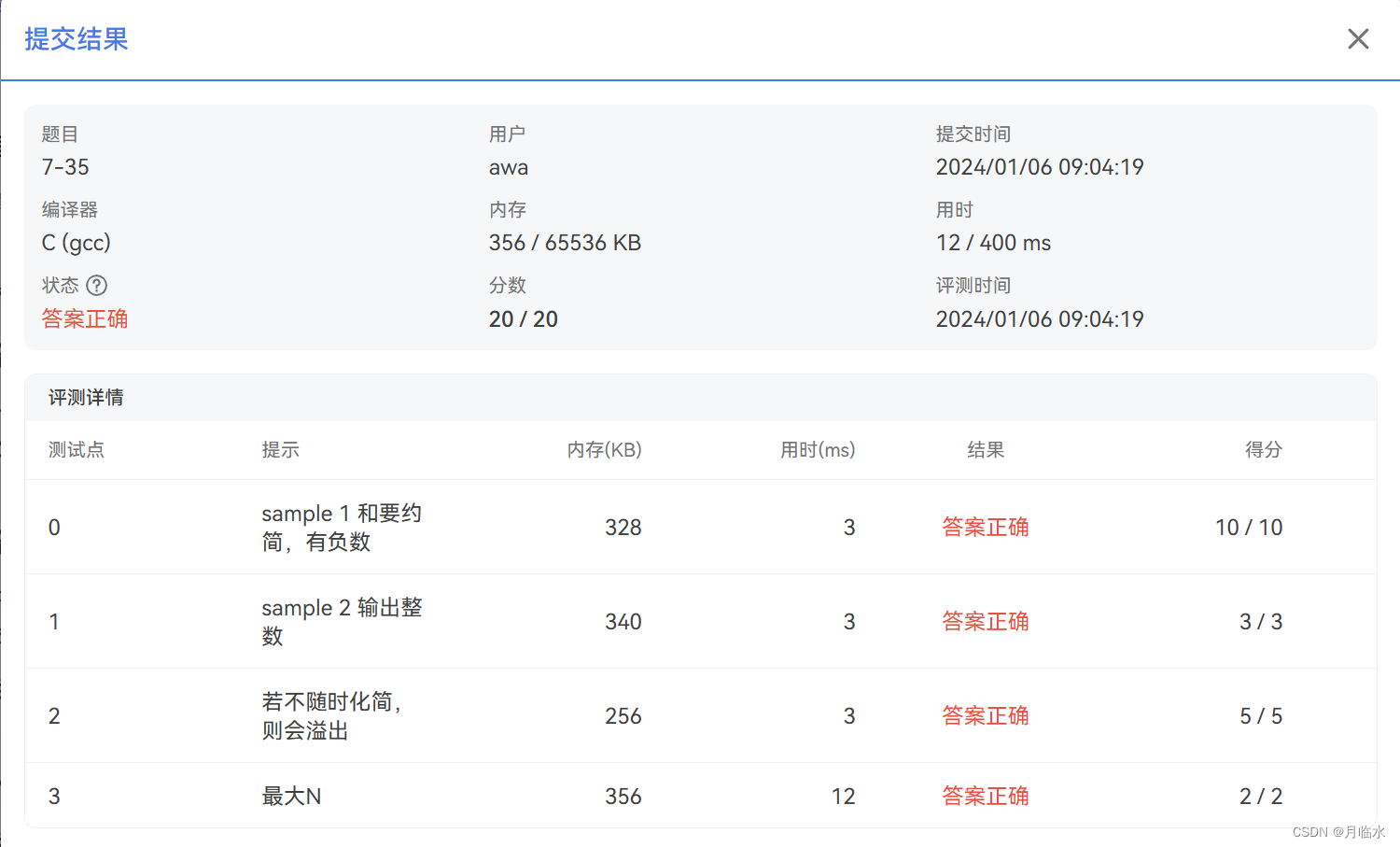
偷懒只能能拿到15分
在这里插入图片描述

思路二：每输入一个分数就化简一次

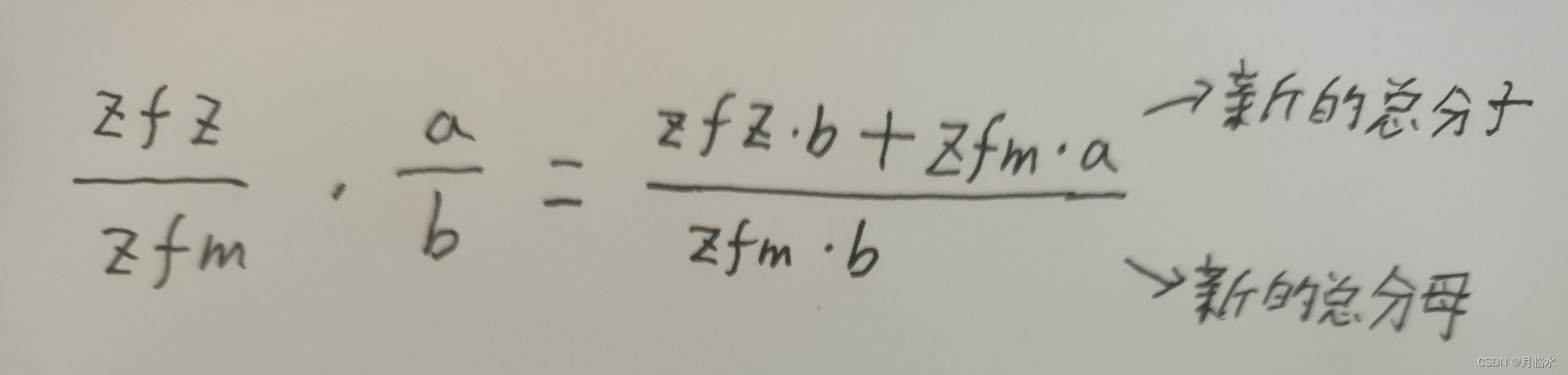
在这里插入图片描述

#include<stdio.h>
void simp(int* x,int* y)//化简分数
{int tmp=*x<*y?*x:*y;while(tmp>1){if(*x%tmp==0&&*y%tmp==0){*x/=tmp;*y/=tmp;break;}tmp--;}
}int main()
{int n =0;scanf("%d",&n);//输入的分数数目int a=0;int b=0;scanf("%d/%d",&a,&b);int zfz=a;int zfm=b;simp(&zfz,&zfm);//化简while(~scanf("%d/%d",&a,&b)){zfz=zfz*b+zfm*a;zfm*=b;simp(&zfz,&zfm);//化简}zfm*=n;//分母乘以n，来计算平均数simp(&zfz,&zfm);if(1==zfm)//如果分母为1，只打印分子就行{printf("%d",zfz);}else if(0==zfz)//如果分子为0，打印0printf("0");elseprintf("%d/%d",zfz,zfm);//正常打印return 0;
}