3D数学基础

学习视频:线性代数的本质 强烈推荐！！

矢量/向量

在笔记中

• 变量使用小写字母表示，a
• 由于笔记中画上箭头表示向量比较麻烦，这里小写字母加粗显示，a
• 矩阵变量使用粗体大写字母表示，A

线性代数围绕向量加法+向量数乘两种基本运算。行矩阵和列矩阵都可以描述向量，在本笔记中，没有特殊说明都是采用行矩阵。

什么是向量

在线性代数中，Vector被称为向量，在几何中，Vector被称为矢量，文中向量矢量都在使用。数字 = 标量，通常用于缩放向量。

向量是空间中的箭头，在线代中，向量经常以原点作为起点。向量的数组表示法[x,y]表示从原点出发(向量起点)如何到达向量终点。

矢量意义
矢量是具有大小和方向的有向线段。

• 矢量的大小：矢量的长度，非负值。
• 矢量的方向：描述矢量在空间中指向的方向。

图形上每个矢量是位置无关的，比如使用笛卡尔坐标描述矢量时，每个坐标相当于描述对应维度(x、y或其他)中有符号位移。
比如三维矢量[3,-1,2]可以表示为①向+x轴平移3个单位②向+y轴平移-1个单位(或者-y轴平移1个单位)③向+z轴平移2个单位。其实顺序不重要，移动的总量是一样的。

矢量可以理解为某种运动方式(二维中沿x轴怎么运动，沿y轴怎么运动)

零矢量：矢量中唯一没有方向的，可以理解为无位移(而不是一个点因为矢量不描述一点)

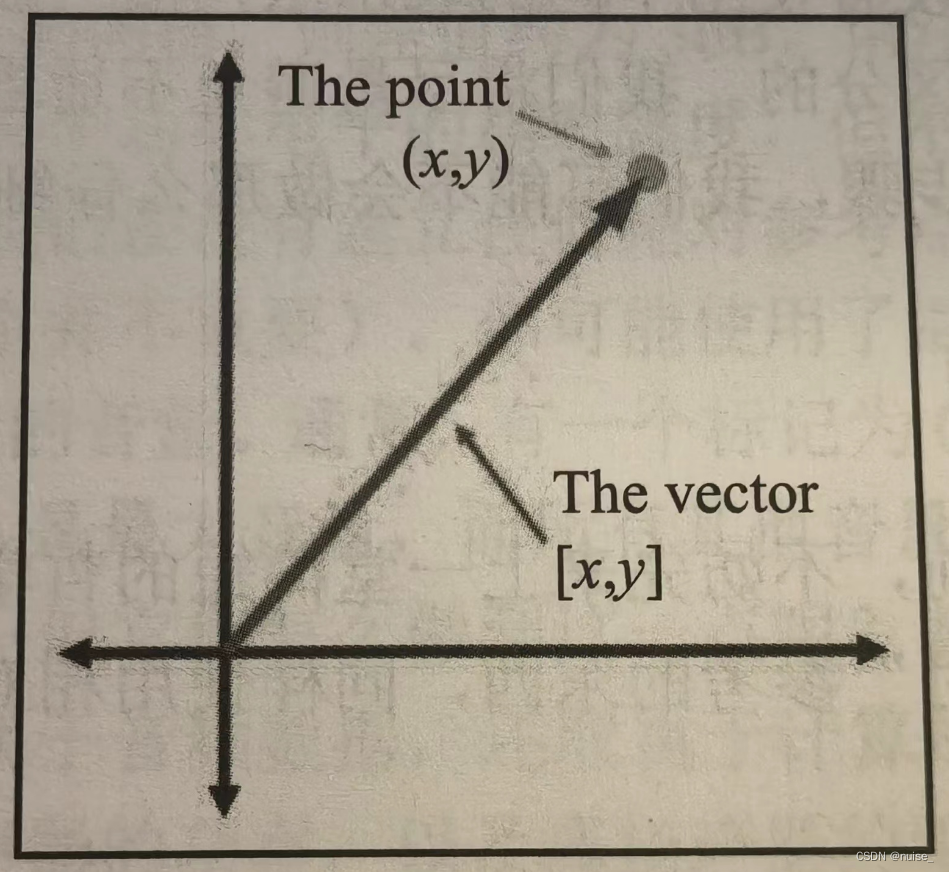
点与矢量的关系

假设有点(x,y)与矢量[x,y]
如果从原点开始按照矢量[x,y]指定的量移动，最终将到达点(x,y)的位置。或者说矢量[x,y]给出了原点到点(x,y)的位移。

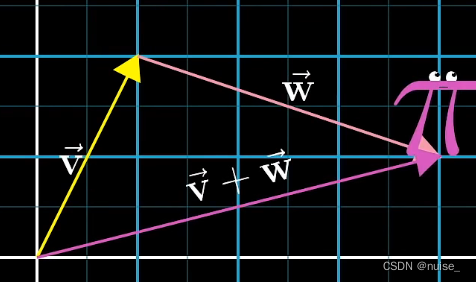
向量基础运算 向量加法

比如v+w，三角形法则几何理解为从一个点开始应用由c指定的位移，然后再应用由w指定的位移，与直接应用v+w指定的位移效果一致。

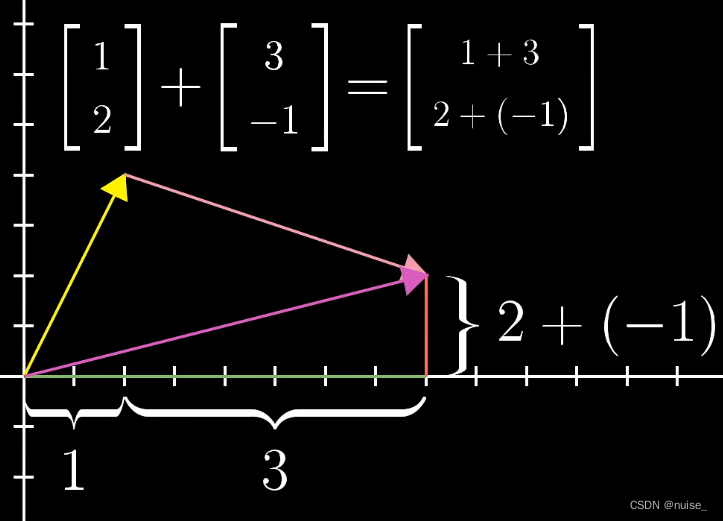
比如在一维轴上，先向右走2步再向右走5步的效果等于直接从原点向右走7步。

假设v=[1,2]、w=[3,-1],v+w表示先沿x轴移动1+3个位移，再沿y轴移动2+(-1)个位移

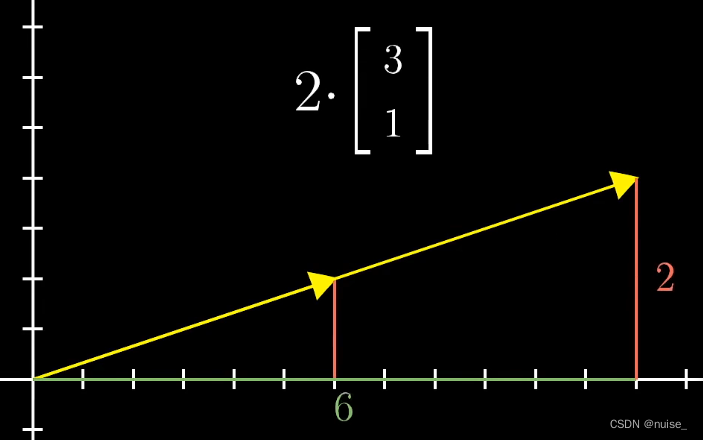
向量基础运算 数乘

运算式：k[x,y,z] = [x,y,z]k = [kx,ky,kz]

数字 = 标量，通常用于缩放向量。

kv表示向量沿指定方向缩放k倍，从数字的角度看，对应于将每一个分量分别*k。
向量与标量相乘就是将向量中的每个分类与标量相乘。

线性组合 - 坐标系的基

假设 i和j是坐标系的基向量
其中
x方向的单位向量i：长度为1，指向+x方向
y方向的单位向量j：长度为1，指向+y方向

并不是说基向量一定是单位向量，空间的一组基严格定义：向量空间的一组基是张成该空间的一个线性无关向量集合

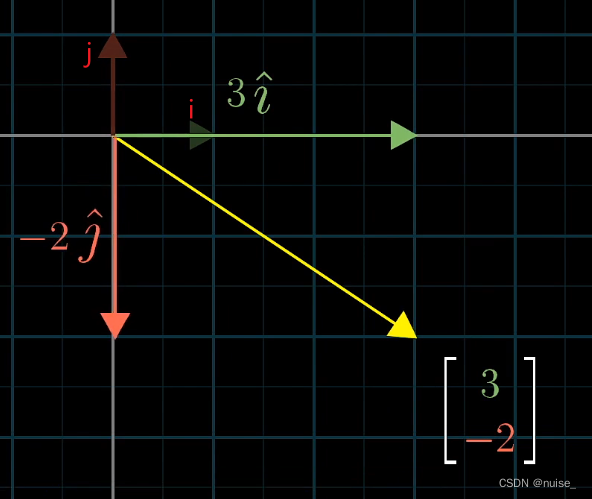
利用坐标系的基，我们可以从另一个角度描述向量。向量可以表示为缩放坐标系的基向量并相加，向量=两个经过缩放的向量和。

将向量v=[3,-2]的分量想象成标量，3表示拉伸i为原来的3倍，-2表示反向拉伸j为原来的两倍。所以向量v = 3i+(-2)j。

如果选择不同的基向量会怎么样？- 张成(Span)的空间

任选两个基向量，使用任意两个标量缩放基向量，然后两基向量相加可以得到所有的二维向量。
当用数字(坐标)描述向量时，都依赖于我们正在使用的基。

比如描述物体的运动时，要依赖参考系。所以用数字描述向量时，要看是在哪个基向量下。

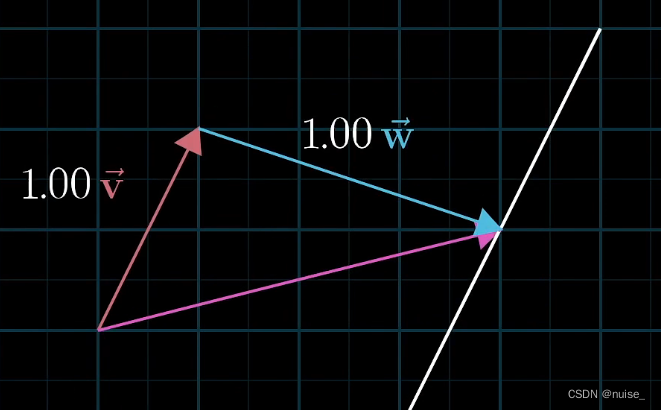
两个数乘向量的和被称为这两个向量的线性组合

为什么叫线性？如果固定住其中一个向量，让另一个向量自由变化，那么向量的终点会描出一条直线。

• 如果同时缩放两个向量，这两个向量并不共线且都不是零向量，那么就可以得到平面中的所有位置。
• 如果两个初始向量共线，产生的向量终点被限制在一条过原点的直线上。
• 如果两个初始向量为零向量，那么产生的向量终点就是原点。

任意两个不共线的向量可以作为平面空间的基底

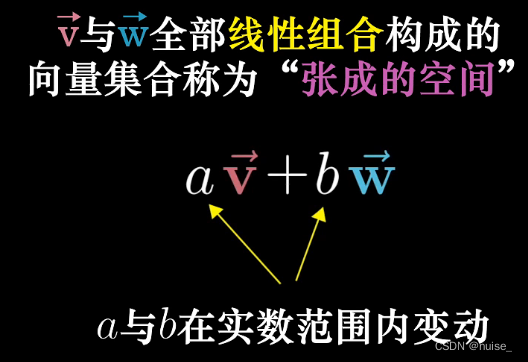
张成(Span)的空间 ：v和w全部线性组合构成的向量集合

是扩张成（张开形成?）的空间吗？感觉这里的张成应该是一个动词？对大部分向量v和w来说，他们张成的空间是所有二维向量的集合，对共线的v和w来说，他们张成的空间是终点落在一条直线上的向量的集合。

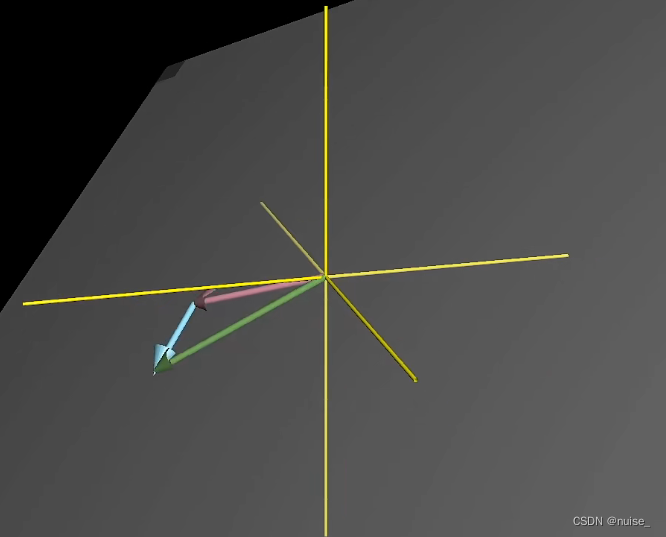
三维向量的张成空间

两个三维向量张成的空间是一个过原点的平面，所有终点落在这个平面上的向量的集合就是这两个向量张成的空间。

三个三维向量张成的空间

1. 第三个向量恰好落在前两个向量所张成的平面上(第三个向量由前两个线性组合形成，可以想象成二维的共线)，张成的空间不会变化还是之前的两个三维向量的张成空间。
2. 如果没有落在前两个向量张成的空间上，这三个三维向量可以描述所有的三维向量(当缩放第三个向量时，前两个向量张成的平面沿着第三个向量的方向来回移动)

线性相关与线性相关

在二维空间的案例中，两个向量共线；在三维空间的案例中，第三个向量恰好落在前两个向量所张成的平面上。

从几何的角度解释线性相关
当有多个向量时，移除其中一个而步减小张成的空间，称这组向量是线性相关的。
其中一个向量可以表示为其他向量的线性组合，因为这个向量已经落在其他向量张成的空间中。

线性无关
二维中的表示就是不共线
三维中的表示就是其中一个向量不在另外两个向量张成的空间中

矩阵与线性变换

线性变换：将输入的向量映射之后输出新的向量，比如映射F(a)=b 表示映射F将a映射到b。
使用变换暗示了可以将这种映射想象成一种运动，比如旋转。

定义：当F满足线性映射时,F(a+b) = F(a)+F(b) 且 F(ka) = F(kb)
描述：将两个矢量相加然后执行变换 = 单独对两个矢量执行变换，然后将变换后的矢量加载一起。缩放一个矢量然后执行变换 = 先变换后缩放

线性变换需要同时具备的性质
1.直线在变换后仍然保持为直线，不能弯曲
2.原点保持固定

矩阵-几何意义线性变换

记录两个基向量i和j变换后的位置，就可以计算出任意向量经过变换后的位置
重要性质：线性变换保持组合系数不变

因为向量之间的关系没变(标量不变)，变的只是基向量
组合系数是特征值？

矩阵只是一个记号，描述了一个线性变换的信息，或者说记录变换后的基向量

案例
假设存在v=[-1,2]，v=-1i+2j，线性变换保持组合系数不变，所以转换后的v = -1转换后的i + 2转换后的j

方阵的几何意义:如果知道一对基如何变换等于知道整个坐标系怎么变换了

• 方阵的行(如果基向量是列向量则是方阵的列)可以理解为坐标空间变换之后的基向量
• 将向量从原始空间变化到新坐标空间的方法是：向量 * 矩阵，矩阵向量乘法就是计算线性变化作用于定向量的一种途径。
• 可通过可视化变化后坐标空间的基矢量来可视化矩阵。

另一个角度理解矩阵乘法的定义

矩阵乘法与线性变换复合

AB：先执行A变换然后执行B变换
如果采用列矩阵表示向量，则先执行B变换再执行A变换。

渲染案例
世界上任何位置和方向都有一个对象，假设希望给定的任意位置和方向上的相机渲染此对象。
前提：取得该对象的顶点(很多顶点)
步骤
1.模型变换，将对象的顶点从对象空间变换到世界空间中
2.视图变换，将世界空间顶点变换到相机空间

Pwld = Pobj Mobj->wld
Pcam = PwldMwld->cam
=> Pcam = Pobj(Mobj->wldMwld->cam)
=> Pcam = Pobj(Mobj->cam)

• AB 不一定等于 BA ：可以将这种变换想象成函数f(g(x))，由于f(g(x)) 不一定等于g(f(x))，所以AB 不一定等于 BA。
• (AB)C = A(BC)：可以将括号理解为将两次变化步骤一次性合并了，但变换的顺序还是一致的。