问题描述
双十一,不仅是购物狂欢节,更有 "光棍节" 之称。这源于 11:1111:11 由四个 11 构成,象征着单身。
作为大学生的小蓝也想经历甜甜的校园恋爱,于是他找到了爱神丘比特,向他祈祷能为自己带来一段邂逅。
丘比特是乐于助人的,他承诺小蓝只要回答出一个简单的数学问题,就完成小蓝的愿望。
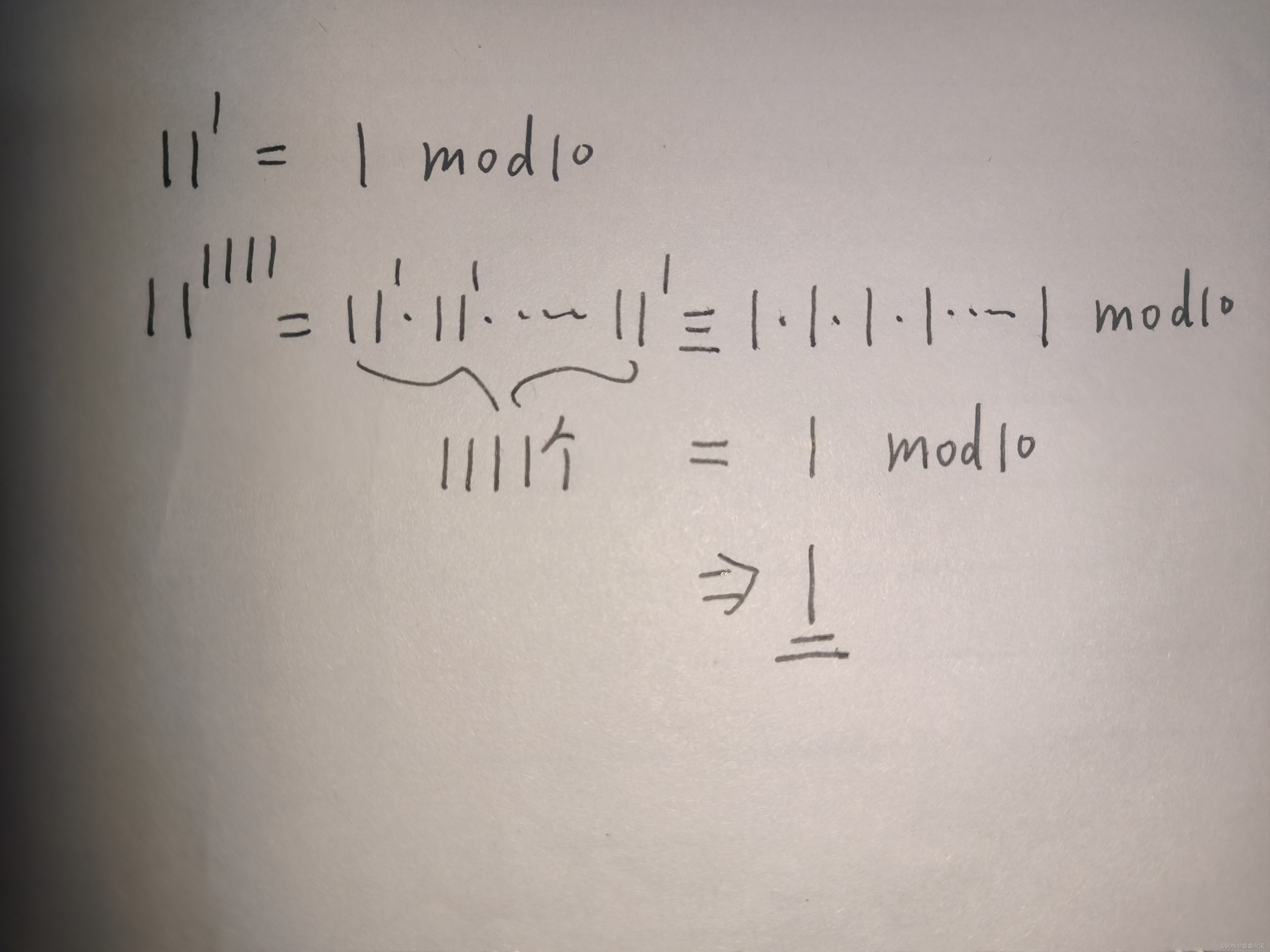
问题是: 111111111111 的 个位数 是多少?
作为小蓝的好朋友,为了小蓝的幸福,请你帮忙解决这个问题。
注意:使用阿拉伯数字作答。
输入格式
本题为填空题,无需输入即可作答(当然如果你单身,你也可以读入一个字符串看看是否有惊喜)。
输出格式
输出一个数字,表示答案。
提示
1×1=11×1=1。
运行限制
| 语言 | 最大运行时间 | 最大运行内存 |
|---|---|---|
| C++ | 1s | 256M |
| C | 1s | 256M |
| Java | 2s | 256M |
| Python3 | 3s | 256M |
| PyPy3 | 3s | 256M |
| Go | 3s | 256M |
| JavaScript | 3s | 256M |
总通过次数: 2225 | 总提交次数: 2300 | 通过率: 96.7%
思路分享:这题是一个数学问题,用数学思路的欧拉定理去做就可以了。

1.基本概念
在证明欧拉定理之前需要先了解几个知识点
1.1 质数
质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数(规定1既不是质数也不是合数)。在数学界,关于质数的研究非常多,最著名便是哥德巴赫猜想
1.2 公约数
公约数,亦称“公因数”。它是指能同时整除几个整数的数 。如果一个整数同时是几个整数的约数,称这个整数为它们的“公约数”;公约数中最大的称为最大公约数。对任意的若干个正整数,1总是它们的公因数。
最大公约数可记为gcd()或()。
1.3 互质
互质是公约数只有1的两个整数,叫做互质整数。公约数只有1的两个自然数,叫做互质自然数,后者是前者的特殊情形。例如,3与5的公约数只有1,所以它们是互质的。可以记为gcd(3,5)=1.
1.4 同余
同余是数论中的重要概念。给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。
1.5 完全剩余系
命 m 为一个自然数,a,b为整数。如果 为 n 的整数倍,则称 a,b 关于 n 同余,用同余式 a ≡ b(mod m) 记之。否则称a,b关于 n 不同余,记为 a ≢ b(mod m)。我们称 n 为同余式的模(modulus)。同余式满足:
反射性(reflection),即 a ≡ a(mod m);
对称性(symmetry),即由 a ≡ b(mod m)可得 b ≡ a(mod m);
传递性(transitivity),即由 a ≡ b(mod m),b ≡ c (mod m)可得 a ≡ c(mod m)。
因此,可以利用同余关系将整数分类,凡同余的数属于一个类,于是异类中的数皆不同余。共得到整数的 n 个类。在每一个类中各取一个数作为代表所成的集合称为模 n 的一个完全剩余系。
代码分享:
#include <iostream>
using namespace std;
int main()
{// 请在此输入您的代码cout<<"1"<<endl;return 0;
}