在本篇中，我将通过一个例子演示在 MATLAB 如何使用 LIME 进行复杂机器学习模型预测结果的解释。

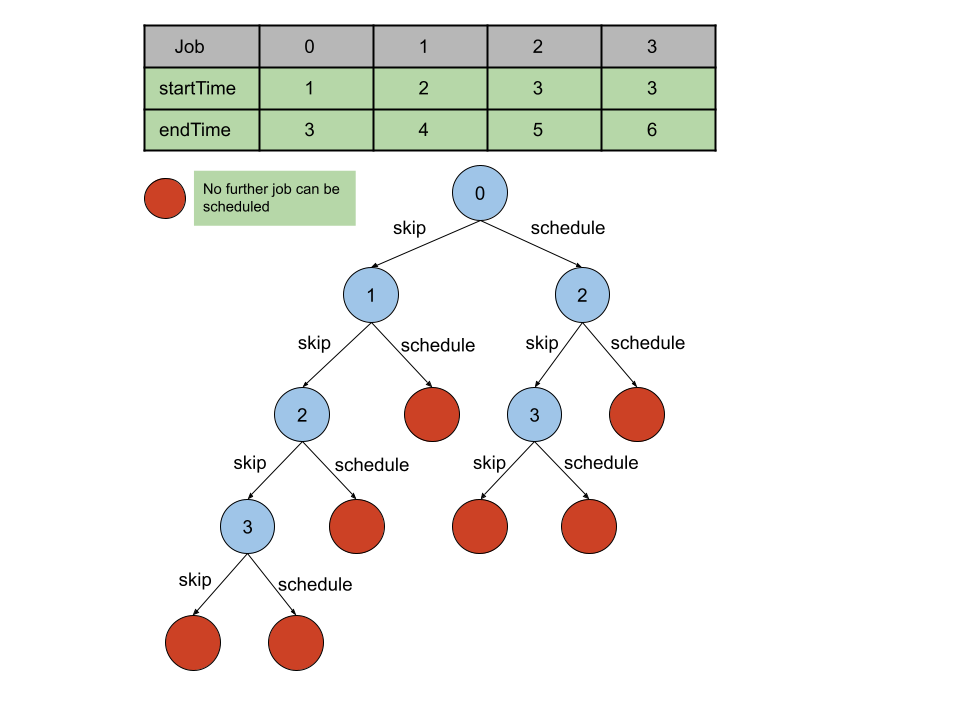
我使用数据集 carbig（MATLAB 自带的数据集）训练一个回归模型，用于预测汽车的燃油效率。数据集 carbig 是 70 年代到 80 年代生产的汽车的一些数据，包括：

其中：MPG 为响应变量（预测结果），其它变量为预测变量（数据特征），训练一个回归模型 f，该回归模型可以通过汽车的气缸数量、排量、生产年份等信息预测汽车的燃油效率，数学表达如下:

MPG = f(Cylinders,Displacement,Horsepower,modelyear,Weight,Acceleration)

利用 LIME 技术对回归模型 f 的预测结果进行解释，查看是那些特征对预测结果产生影响。具体的实现过程如下。

训练机器学习模型

导入数据集并构建数据表：

rng(0);

load carbig

tbl =table(Acceleration,Cylinders,Displacement,…

Horsepower,Model_Year,Weight,MPG);

进行数据预处理，去除带有缺失值的行：

tbl =rmmissing(tbl);

生成变量数据表：

tblX =removevars(tbl,'MPG');

head(tblX)

将变量按数据类型进行划分。其中第二列 Cylinders 和第五列 Model_Year 是分类变量，其它列是数值变量

tblX_num= removevars(tblX,{'Cylinders','Model_Year'});

tblX_cate= tblX(:,{'Cylinders','Model_Year'});

对于数值变量查看变量之间的相关性

cor =corr(tblX_num{:,:});

h =heatmap(cor);

h.XDisplayLabels= tblX_num.Properties.VariableNames;

h.YDisplayLabels= tblX_num.Properties.VariableNames;

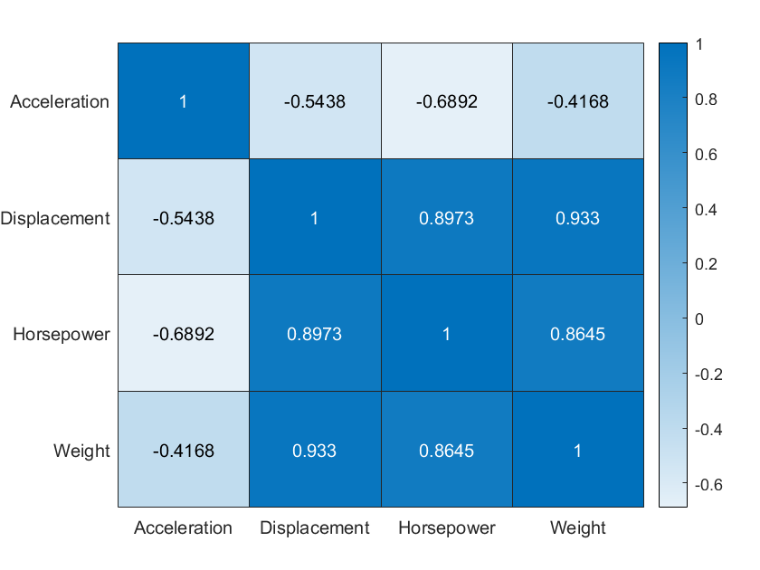
 图 1

从图 1 的计算结果得出，Displacement 与 Weight 具有强相关性，Displacement 与 Horsepower 的相关性也较大。因此，去除 Displacement 变量。

tblX_num= removevars(tblX_num,{'Displacement'});

再次计算变量之间的相关性：

cor =corr(tblX_num{:,:});

h =heatmap(cor);

h.XDisplayLabels= tblX_num.Properties.VariableNames;

h.YDisplayLabels= tblX_num.Properties.VariableNames;

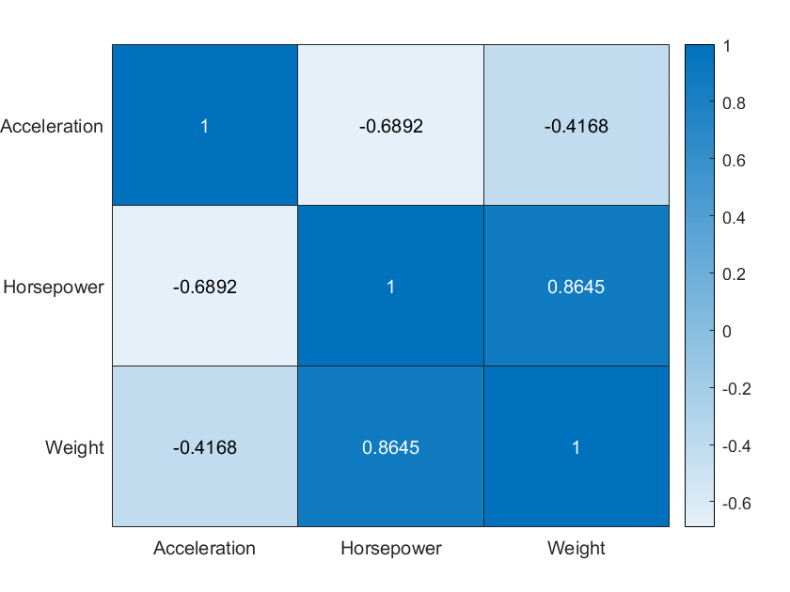
图 2

图 2 显示，变量之间的相关性都小于 0.9，因此保留相关性小于 0.9 的变量作为预测变量。

对数值型预测变量进行标准化，缩放到[0,1]之间，以消除量纲对预测结果的影响。

tblX_num= normalize(tblX_num,"range");

tbl.MPG =normalize(tbl.MPG,"range");

head(tblX_num)

将数值变量和分类变量合并成训练数据集：

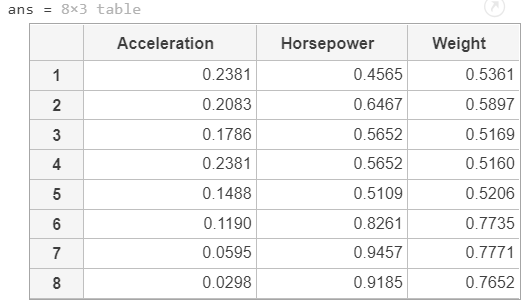
将数值变量和分类变量合并成训练数据集：

tblX =[tblX_num tblX_cate];

head(tblX)

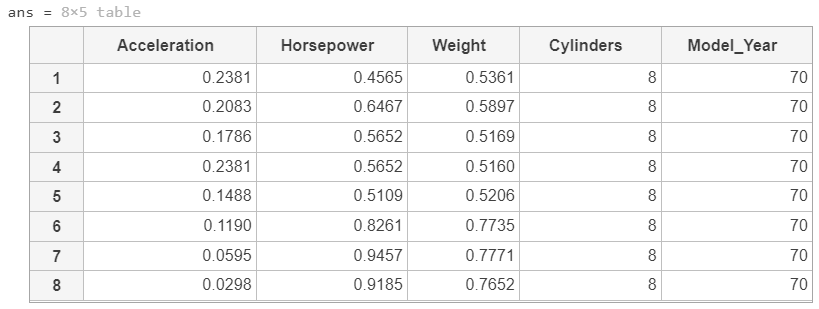
训练一个随机森林回归模型，预测变量是表 tblX 中的变量，响应变量是 MPG，并指明第 4 和第 5 列是分类变量。

mdl_bag= fitrensemble(tblX,tbl.MPG,'Method',"Bag",…

'CategoricalPredictors',[4 5]);

对机器学习模型进行解释

利用 LIME 对训练好的回归模型进行解释。

首先构建使用 lime 函数构建一个 LIME，简单的解释模型选择决策树，同时 lime 中也指明了原始回归模型的训练样本的第 4 和第 5 列是分类变量。

lime_bag = lime(mdl_bag,'CategoricalPredictors',[4 5],…        'SimpleModelType',"tree");

我们从训练集中选取一个样本作为预测数据（即 QueryPoint），测试模型的预测结果，以及模型的解释结果。选择训练集中的第 257 个样本作为预测数据。

num =257;

queryPoint= tblX(num,:)

以预测数据为基础生成合成数据，并训练一个可解释模型（决策树模型）。对于可解释模型，指定变量个数为 5。也就是说，我们最多只分析 5 个对预测结果产生影响的变量。

lime_bag= fit(lime_bag,queryPoint,5);

根据预测变量对预测结果的影响程度进行排序并可视化。

f =plot(lime_bag);

title('随机森林回归模型的LIME');

f.CurrentAxes.TickLabelInterpreter= 'none';

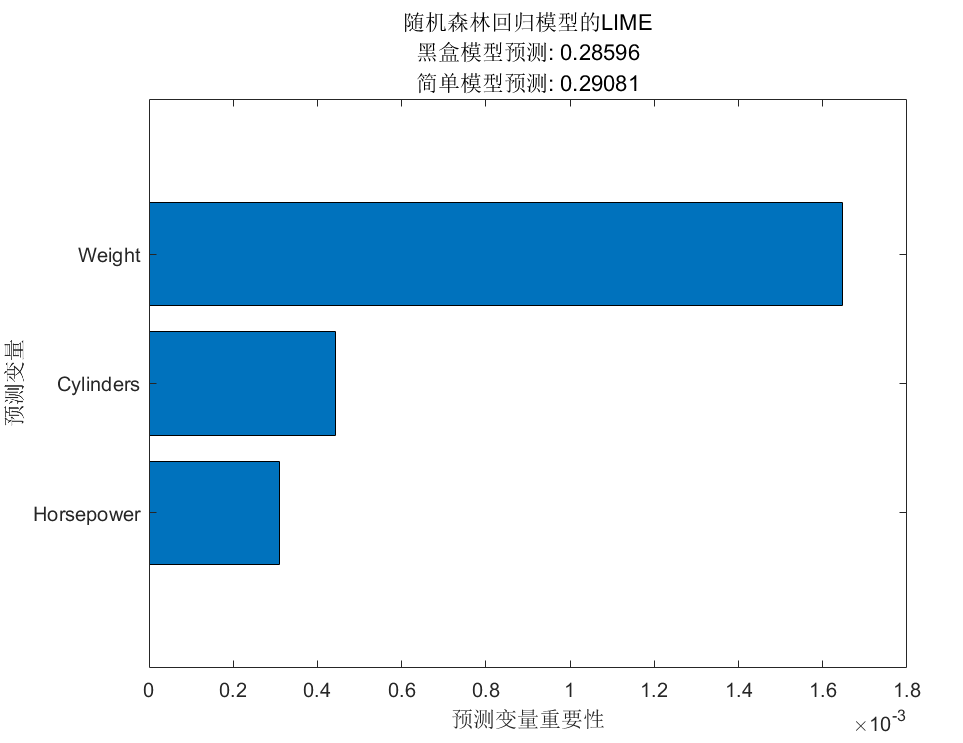
图 3

从图 3 可以看出，预测变量 Weight，对回归模型预测的结果影响最大，其次是 Cylinders 和 Horsepower。

可以解释为：基于输入数据预测出的汽车燃油效率，主要依次考虑了汽车的重量（Weight）、汽车的动力（Horsepower）、汽车汽缸数量（Cylinders）。

这种解释也是符合我们的先验知识：汽车自重越大燃油效率越低，也就是每加仑行驶的里程数越少。汽车功率越大、汽缸数量越多，耗油越大。

因此说，回归模型预测的结果是可信的。