1329：【例8.2】细胞广度优先搜索-编程知识

1329：【例8.2】细胞广度优先搜索

1329：【例8.2】细胞

时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
一矩形阵列由数字0
到9组成,数字1到9
代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。如:
4 10
0234500067
1034560500
2045600671
0000000089
有4个细胞。

【输入】
第一行为矩阵的行n和列m;
下面为一个n×m的矩阵。
【输出】
细胞个数。

【输入样例】
4 10
0234500067
1034560500
2045600671
0000000089
【输出样例】
4

解析：
题意可知：只要是上下左右相邻都是不为0数字，即为同一种细胞（我第一次读以为只有上下左右有数字不为0，才能算一种细胞emmmm傻狗）

如果把该二位数组每个位置视为节点，则题目思路如下：

可以用深度优先算法：从第一个节点开始遍历，然后分别判断其上下左右是否有相邻的。dfs的精髓就是每次再判断这个节点的数的‘邻居’是否其相邻是同一细胞时，只要是，就立即dfs该‘邻居’,，继续dfs，直到判断完成，又回溯到上一个节点，判断其上下左右。
也可以用广度优先算法：从一个节点开始遍历，然后分别判断其上下左右是否是同一种细胞，如果是，则上下左右判断完后，再判断该节点的上下左右（即该节点的上面一个节点）
- 而表示这个遍历了上下左右后再回到该节点就需要用到队列（先进先出）
- 可以用一个结构体队列，将下标(x,y）遍历时入队，然后判断四个方向，如果是同一种细胞则压入队列，四个方向遍历完后，回到队列头部，将其出队（q.pop()）,然后又从队头开始去判断其四个方向，，，，直到该队列为空，说明这一种细胞已经搜索完了（由于队列的顺序性，也可以不用结构体数组，直接分别将x,y分别压入队列，在获取到队头的x后，及时Pop（），也可以通过q.front()拿到y,所以可以不用结构体数组）
不管是哪个搜索，都可以在搜索到一个节点时，及时标注（用一个数组去记录是否访问过），减少遍历时间。由于此题特殊，可以直接将数组值设为0,也可以在搜索完成后不会出现二次遍历的情况

代码示例：

深度优先搜索

//深搜-样例比较小时可以用 
#include<bits/stdc++.h>
using namespace std;
#define N 101
int n,m,num;
char a[N][N];
int dx[4]={-1,1,0,0};  //上、下、左、右四个方向 
int dy[4]={0,0,-1,1};
void dfs(int x,int y);
int main()
{cin>>n>>m; for(int i=0;i<n;i++)scanf("%s",&a[i]);//遍历每个元素，用标记数组标记已经访问过的，则可以避免二次遍历 ，减缩短运行时间 for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(a[i][j]!='0'){num++;    //没被访问过说明是新的不同的细胞 dfs(i,j); //搜索这一元素的四个方向}}}cout<<num;return 0;
}
void dfs(int x,int y)
{a[x][y]='0';//为0即也表示该细胞已经访问过了 int newx,newy;for(int i=0;i<4;i++){newx=x+dx[i];newy=y+dy[i];//首先保证在边界内，其次保证他是细胞，最后保证他是未被访问过的 ，都满足即可继续访问其周围的细胞 if(newx<n && newx>=0 && newy<m && newy>=0&&a[newx][newy]!='0')  {dfs(newx,newy);}}
}

广度优先搜索

//广搜 
#include<bits/stdc++.h>
using namespace std;
#define N 101
int n,m,num;
char a[N][N];
int dx[4]={-1,1,0,0};  //上、下、左、右四个方向 
int dy[4]={0,0,-1,1};	
queue<int>q;//数据类型为int的队列 -先进先出 
void bfs(int x,int y);
int main()
{cin>>n>>m; for(int i=0;i<n;i++)scanf("%s",&a[i]);for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(a[i][j]!='0'){num++;    //没被访问过说明是新的不同的细胞 bfs(i,j); //搜索这一元素的四个方向}}}cout<<num;return 0;
}
void bfs(int x,int y)
{a[x][y]='0';//表示访问过 ,在这里不会影响入队后的周围细胞的判断，因为一次bfs就完成了同一个细胞的问题 q.push(x),q.push(y);//将下标分别压入队列（属于同一个细胞队列） int newx,newy;//同一个细胞队列，先拿到队列的数据，出队处理，然后一次访问四个方向(立即出队便于后面同一种细胞进来，保证每次循环处理的是新一个细胞) while(!q.empty()){int nx=q.front();  q.pop();int ny=q.front();q.pop();for(int i=0;i<4;i++){newx=nx+dx[i],newy= ny+dy[i];if(newx<n && newx>=0 && newy<m && newy>=0&&a[newx][newy]!='0') {//继续压入栈（是同一个细胞）q.push(newx);q.push(newy);a[newx][newy]='0';//只是压入同一个细胞的栈，不会继续搜索，所以要标记为以访问，避免重复访问 }}} }

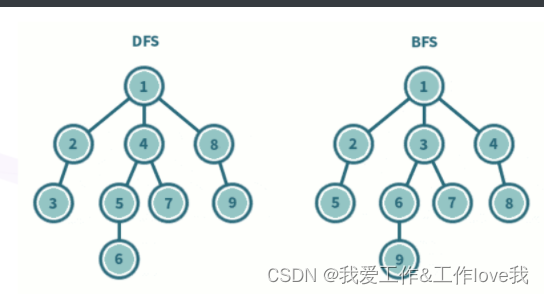
深度优先算法BFS是一种图像搜索演算法，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，主要借助一个队列、一个布尔类型数组、邻接矩阵完成**。
从图像来看，他是先一个节点搜索所有的子节点遍历完毕后，再回到同层次的第一个的节点再次遍历其所有子节点。
在实际运用时，遍历子节点的过程实质是求完一个情况的所有相邻的解，再开始搜索下一个节点

以下是bfs和dfs的树遍历对比
在这里插入图片描述