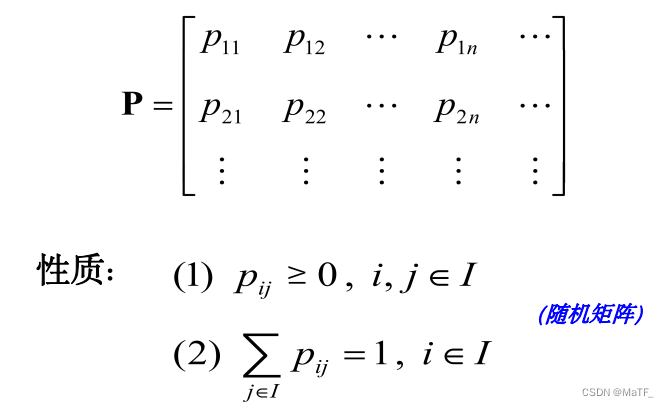参考资料:
- 《机器学习》周志华
- https://zhuanlan.zhihu.com/p/27056207
1 马尔可夫链
1.1 定义

直观含义:在已知现在的条件下,过去与未来相互独立。
1.2 马尔可夫模型

根据定义,A 必为方阵
其中, p i j ( n ) = P { X n + 1 = j ∣ X n = i } p_{ij}(n)=P\lbrace X_{n+1}=j|X_n=i\rbrace pij(n)=P{Xn+1=j∣Xn=i}称为一步转移概率。

n n n 步转移的性质: P ( n ) = P n P^{(n)}=P^n P(n)=Pn

p j ( n ) = ∑ i ∈ I p i p i j n = P T ( 0 ) P ( n ) p_j(n)=\sum\limits_{i\in I}p_ip_{ij}^n=P^T(0)P^{(n)} pj(n)=i∈I∑pipijn=PT(0)P(n)
1.3 例


2 隐马模型(HMM)
2.1 模型定义
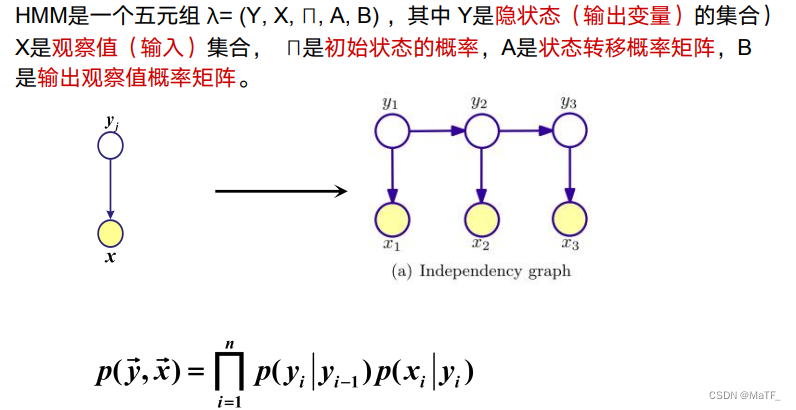

2.2 基本问题

2.3 相关算法
2.3.1 前向算法(问题一)
给定隐马模型 λ \lambda λ ,定义时刻 t t t 为止的观测序列为 x 1 , x 2 , ⋯ , x t x_1, x_2,\cdots,x_t x1,x2,⋯,xt ,且状态为 i i i 的概率为前向概率,即:
α t ( i ) = P ( x 1 , x 2 , ⋯ , x t , y t = i ∣ λ ) \alpha_t(i)=P(x_1,x_2,\cdots,x_t,y_t=i|\lambda) αt(i)=P(x1,x2,⋯,xt,yt=i∣λ)
算法流程:
- 初值: α 1 ( i ) = π i b i ( x 1 ) \alpha_1(i)=\pi_ib_i(x_1) α1(i)=πibi(x1)
- 递推式: α t + 1 ( i ) = [ ∑ j = 1 N α t ( j ) a i j ] b i ( x t + 1 ) \alpha_{t+1}(i)=\big[\sum\limits_{j=1}^{N}\alpha_t(j)a_{ij}\big]b_i(x_{t+1}) αt+1(i)=[j=1∑Nαt(j)aij]bi(xt+1)
- 终止: P ( O ∣ λ ) = ∑ i = 1 N α n ( i ) P(O|\lambda)=\sum\limits_{i=1}^{N}\alpha_n(i) P(O∣λ)=i=1∑Nαn(i)
2.3.2 后向算法(问题一)
给定隐马模型 λ \lambda λ ,定义时刻 t t t 状态为 i i i 的条件下, t + 1 t+1 t+1 到 n n n 的部分观测序列为 x t + 1 , x t + 2 , ⋯ , x n x_{t+1},x_{t+2},\cdots,x_{n} xt+1,xt+2,⋯,xn的概率为后向概率,即:
β t ( i ) = P ( x t + 1 , x t + 2 , ⋯ , x n ∣ y t = i , λ ) \beta_t(i)=P(x_{t+1},x_{t+2},\cdots,x_{n}|y_t=i,\lambda) βt(i)=P(xt+1,xt+2,⋯,xn∣yt=i,λ)
算法流程:
- 初值: β n ( i ) = 1 \beta_n(i)=1 βn(i)=1
- 递推式: β t ( i ) = ∑ j = 1 N a i j b j ( x t + 1 ) β t + 1 ( j ) \beta_t(i)=\sum\limits_{j=1}^{N}a_{ij}b_j(x_{t+1})\beta_{t+1}(j) βt(i)=j=1∑Naijbj(xt+1)βt+1(j)
- 终止: P ( O ∣ λ ) = ∑ i = 1 N π i ∗ b 1 ( x 1 ) ∗ β 1 ( i ) P(O|\lambda)=\sum\limits_{i=1}^{N}\pi_i*b_1(x_1)*\beta_1(i) P(O∣λ)=i=1∑Nπi∗b1(x1)∗β1(i)
本质上都是全概率公式!
2.3.3 Viterbi算法(问题二)

算法流程:
- 初值: δ 1 ( i ) = π i b i ( x 1 ) , ψ 1 ( i ) = 0 \delta_1(i)=\pi_ib_i(x_1),\ \psi_1(i)=0 δ1(i)=πibi(x1), ψ1(i)=0
- 递推式: δ t + 1 ( i ) = max 1 ≤ j ≤ N δ t ( j ) a j i b i ( x t + 1 ) , δ t + 1 ( i ) = arg max 1 ≤ j ≤ N δ t ( j ) a j i b i ( x t + 1 ) \delta_{t+1}(i)=\max\limits_{1\le j\le N}\delta_t(j)a_{ji}b_{i}(x_{t+1}),\ \delta_{t+1}(i)=\argmax\limits_{1\le j\le N}\delta_t(j)a_{ji}b_{i}(x_{t+1}) δt+1(i)=1≤j≤Nmaxδt(j)ajibi(xt+1), δt+1(i)=1≤j≤Nargmaxδt(j)ajibi(xt+1)
- 最优路径: y t ∗ = ψ t + 1 ( y t + 1 ∗ ) y_t^*=\psi_{t+1}(y^*_{t+1}) yt∗=ψt+1(yt+1∗)(倒推得到最优路径)
算法解释:https://www.zhihu.com/question/20136144
该算法似乎适用于在全连通图上找最短路?
2.3.4 Baum-Welch算法(问题三)
给定 HMM 和观察序列,定义 ξ t ( i , j ) \xi_t(i,j) ξt(i,j) 为在时间 t t t 位于状态 i i i ,时间 t + 1 t+1 t+1 位于状态 j j j 的概率:
ξ t ( i , j ) = P ( y t = i , y t + 1 = j ∣ X , λ ) = P ( y t = i , y t + 1 = j , X ∣ λ ) P ( X ∣ λ ) = α t ( i ) a i j b j ( x t + 1 ) β t + 1 ( j ) P ( X ∣ λ ) = α t ( i ) a i j b j ( x t + 1 ) β t + 1 ( j ) ∑ i = 1 N ∑ j = 1 N α t ( i ) a i j b j ( x t + 1 ) β t + 1 ( j ) \begin{align} \xi_t(i,j)&=P(y_t=i,y_{t+1}=j|X,\lambda)\\ &=\frac{P(y_t=i,y_{t+1}=j,X|\lambda)}{P(X|\lambda)}\\ &=\frac{\alpha_t(i)a_{ij}b_j(x_{t+1})\beta_{t+1}(j)}{P(X|\lambda)}\\ &=\frac{\alpha_t(i)a_{ij}b_j(x_{t+1})\beta_{t+1}(j)}{\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_t(i)a_{ij}b_j(x_{t+1})\beta_{t+1}(j)} \end{align} ξt(i,j)=P(yt=i,yt+1=j∣X,λ)=P(X∣λ)P(yt=i,yt+1=j,X∣λ)=P(X∣λ)αt(i)aijbj(xt+1)βt+1(j)=i=1∑Nj=1∑Nαt(i)aijbj(xt+1)βt+1(j)αt(i)aijbj(xt+1)βt+1(j)
(2)→(3)利用了乘法原理,即先到达状态 i i i ,再由状态 i i i 转移到 状态 j j j ,然后在状态 j j j 下取到观测值 x t + 1 x_{t+1} xt+1 ,再从状态 j j j 得到剩下的观测值。
(3)→(4)利用了全概率公式
疑问:既然已经得到了 α , β \alpha,\beta α,β ,为啥不直接通过 α n \alpha_n αn 或 β 1 \beta_1 β1 求呢?
给定 HMM 和观察序列,在时间 t t t 位于状态 i i i 的概率为:
γ t ( i ) = ∑ j = 1 N ξ t ( i , j ) \gamma_t(i)=\sum\limits_{j=1}^{N}\xi_t(i,j) γt(i)=j=1∑Nξt(i,j)

参数的更新可由 EM 算法推导出来,不过直观上也是比较容易理解的。