💡💡💡全网独家首发创新(原创),纯自研模块,适合paper !!!
💡💡💡内涵CBAM注意力改进、ECA改进,SPPF改进等!!!

全网首发独家原创
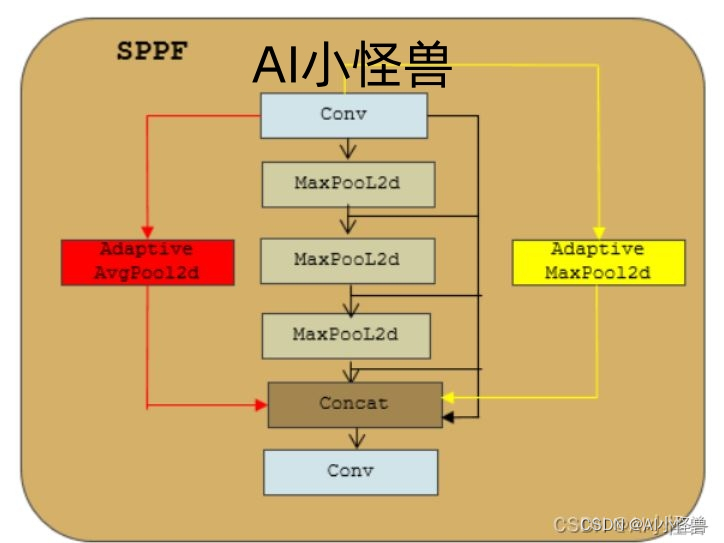
1.SPPF创新结构
重新设计全局平均池化层和全局最大池化层,增强全局视角信息和不同尺度大小的特征
分析SPPF的问题点,只关注边缘信息而忽略背景信息
如何改进:
我们在SPPF模块的基础上,利用全局平均池化层和全局最大池化层,加入一些全局背景信息和边缘信息,帮助网络更好的做出判断。
YOLOv8实现SPPF创新实现
YOLOv5实现SPPF创新实现
YOLOv7实现SPPF创新实现
2.创新自研CPMS注意力
多尺度通道注意力具+多尺度深度可分离卷积空间注意力,全面升级CBAM
CPMS | 亲测在多个数据集能够实现涨点,对标CBAM。
在道路缺陷检测任务中,原始map为0.8,cbam为0.822 ,CPMS 为 0.874
CPMS注意力结构图
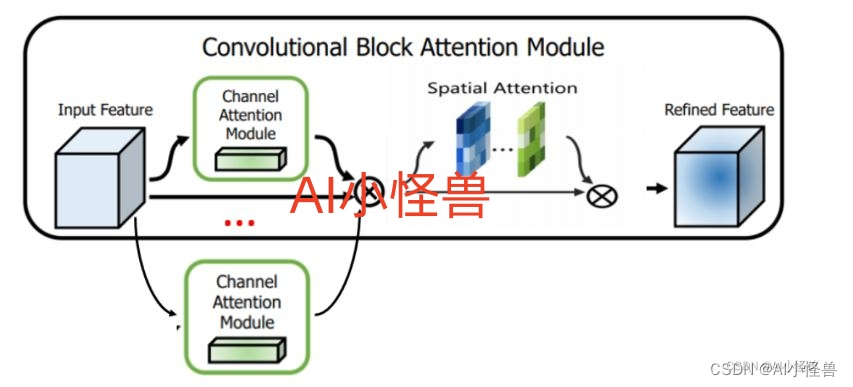
原始CBAM结构图:
 YOLOv8 CPMS实现
YOLOv8 CPMS实现
YOLOv5 CPMS实现
YOLOv7 CPMS实现
3.MSAM(CBAM升级版)
通道注意力具备多尺度性能,多分支深度卷积更好的提取多尺度特征,最后高效结合空间注意力
MSCA | 亲测在多个数据集能够实现涨点,对标CBAM。
在道路缺陷检测任务中,原始map为0.8,cbam为0.822 ,MSCA 为 0.855

YOLOv8实现MSAM注意力实现
YOLOv5实现MSAM注意力实现
YOLOv7实现MSAM注意力实现
4.高效率通道注意力EMCA
一种新颖的跨通道交互的高效率通道注意力EMCA,ECA改进版
EMCA结构图:

ECA结构图:

YOLOv8实现EMCA注意力实现
YOLOv5实现EMCA注意力实现
YOLOv7实现EMCA注意力实现
5. 自研独家创新FT_Conv
卷积高效结合分数阶变换
卷积如何有效地和频域结合,引入分数阶傅里叶变换(FrFT)和分数阶Gabor变换(FrGT),最终创新到YOLOv8。
在道路缺陷检测任务中,原始map为0.8,FT_Conv为0.82
YOLOv8实现FT_Conv实现
YOLOv5实现FT_Conv实现
YOLOv7实现FT_Conv实现
6.自研独家创新BSAM注意力
提出新颖的注意力BSAM(BiLevel Spatial Attention Module),创新度极佳,适合科研创新,效果秒杀CBAM,Channel Attention+Spartial Attention升级为新颖的 BiLevel Attention+Spartial Attention

YOLOv8实现BSAM注意力实现
YOLOv5实现BSAM注意力实现
YOLOv7实现BSAM注意力实现
原创性专栏介绍
💡💡💡全网独家首发创新(原创),适合paper !!!
💡💡💡 2024年计算机视觉顶会创新点适用于Yolov5、Yolov7、Yolov8等各个Yolo系列,专栏文章提供每一步步骤和源码,轻松带你上手魔改网络 !!!
💡💡💡重点:通过本专栏的阅读,后续你也可以设计魔改网络,在网络不同位置(Backbone、head、detect、loss等)进行魔改,实现创新!!!
YOLOv8原创自研
https://blog.csdn.net/m0_63774211/category_12511737.html?spm=1001.2014.3001.5482

YOLOv5原创自研
https://blog.csdn.net/m0_63774211/category_12511931.html

YOLOv7原创自研
https://blog.csdn.net/m0_63774211/category_12511937.html