因子化简

题目背景
质数（又称“素数”）是指在大于 1的自然数中，除了 1和它本身以外不再有其他因数的自然数。

问题描述
小 P 同学在学习了素数的概念后得知，任意的正整数 n都可以唯一地表示为若干素因子相乘的形式。如果正整数 n有 m个不同的素数因子 p1,p2,…pm，则可以表示为：n = (p1^t1) x (p2^t2) x … x (pm^tm)。

小 P 认为，每个素因子对应的指数 ti反映了该素因子对于 n的重要程度。现设定一个阈值 k，如果某个素因子 pi 对应的指数 ti小于 k，则认为该素因子不重要，可以将 pi^ti项从 n中除去；反之则将 pi^ti项保留。最终剩余项的乘积就是n简化后的值，如果没有剩余项则认为简化后的值等于 1。

试编写程序处理 q个查询：

每个查询包含两个正整数 n和 k，要求计算按上述方法将 n简化后的值。
输入格式
从标准输入读入数据。

输入共 q + 1行。

输入第一行包含一个正整数 q，表示查询的个数。

接下来 q行每行包含两个正整数 n和 k，表示一个查询。

输出格式
输出到标准输出。

输出共 q行。

每行输出一个正整数，表示对应查询的结果。

样例输入

3
2155895064 3
2 2
10000000000 10

样例输出

2238728
1
10000000000

样例解释
查询一：

其中素因子 3指数为 2，107 指数为 1。将这两项从 n中除去后，剩余项的乘积为 。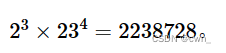

查询二：

所有项均被除去，输出 1。

查询三：

所有项均保留，将 n原样输出。

子任务
40% 的测试数据满足：n <= 1000；

80% 的测试数据满足：n <= 10^5；

全部的测试数据满足：1 < n <= 10^10 且 1 < k ,q <= 10。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
ll n;
ll x;
int q,k;
ll ans = 1;ll qmi(ll a,ll b)
{ll res = 1;while(b){if(b & 1) res = res * a;a = a * (ll)a;b = b >> 1;}return res;
}void divide(ll x)
{for(ll i=2;i<=x/i;i++){if(x%i == 0){ll res = 0;while(x%i == 0){x /= i;res++;}// cout<<i<<" "<<res<<endl;if(res >= k) ans *= (ll)qmi(i,res);// cout<<i<<" "<<res<<endl;// cout<<(ll)i*i<<endl;}}// if(x>1)// {//     cout<<x<<" "<<"1"<<endl;// }cout<<ans<<endl;
}int main()
{cin>>q;while(q--){ans = 1;cin>>n>>k;divide(n);}return 0;
}