大纲
- 3维数组切分
- 打平重组法
- 深度切分法
- 3维数组堆叠
我们在用手机拍照片时,往往会对照片进行滤镜处理,从而让照片更加美观。本文我们将实现几种滤镜效果——去除所有像素中的某一种原色,形成只有红绿、红蓝和绿蓝原色的照片。
为了突出色彩丰富性,我们借用梵高的《星空》为测试照片。

在《使用numpy处理图片——基础操作》一文中,我们介绍了RGBA色彩空间模型。本文我们将忽略Alpha通道,只考虑RGB模型。于是我们得到的数组将是height * width * 3,其中的3是RGB的值所在的维度长度。
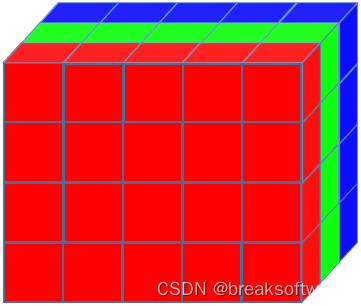
我们希望把上图中不同原色的数组进行切分,然后通过不用原色的组合获得新图片。

这儿涉及两个问题:
- 三维数组切分
- 三维数组堆叠
3维数组切分
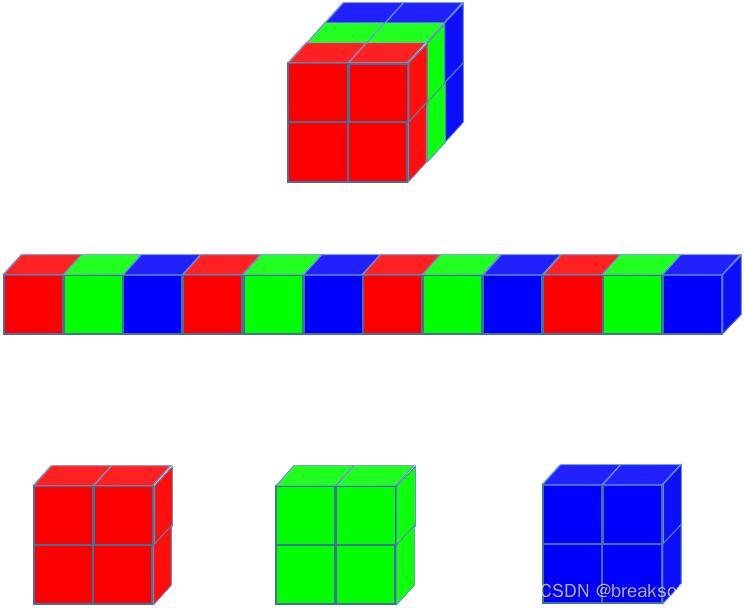
3维数组切分有两种方法。一种是将三维数组打平,然后切片找到相同原色对应的元素,最后重组出长宽不变,但是深度为1的3维数组,我们称之为打平重组法;另外一种就是按深度进行切分,我们称之为深度切分法。
打平重组法
import numpy as np
from PIL import Imageimg = Image.open('the_starry_night.jpg')
data = np.array(img)dataOneDim = data.reshape(data.size)
red = dataOneDim[0::3].reshape((data.shape[0], data.shape[1], 1))
green = dataOneDim[1::3].reshape((data.shape[0], data.shape[1], 1))
blue = dataOneDim[2::3].reshape((data.shape[0], data.shape[1], 1))
我们对dataOneDim中元素进行选择,红色(R)位于RGB的第一位,所以下标是0;绿色(G)位于RGB的第二位,所以下标是1;蓝色(B)位于RGB的第三位,所以下标是2。然后每隔3个元素把所有相同原色的元素挑选出来。
深度切分法
import numpy as np
from PIL import Imageimg = Image.open('the_starry_night.jpg')
data = np.array(img)colorDim3List = np.dsplit(data, 3)
red = colorDim3List[0]
green = colorDim3List[1]
blue = colorDim3List[2]
这儿我们使用dsplit方法,在第三个维度上进行切分。
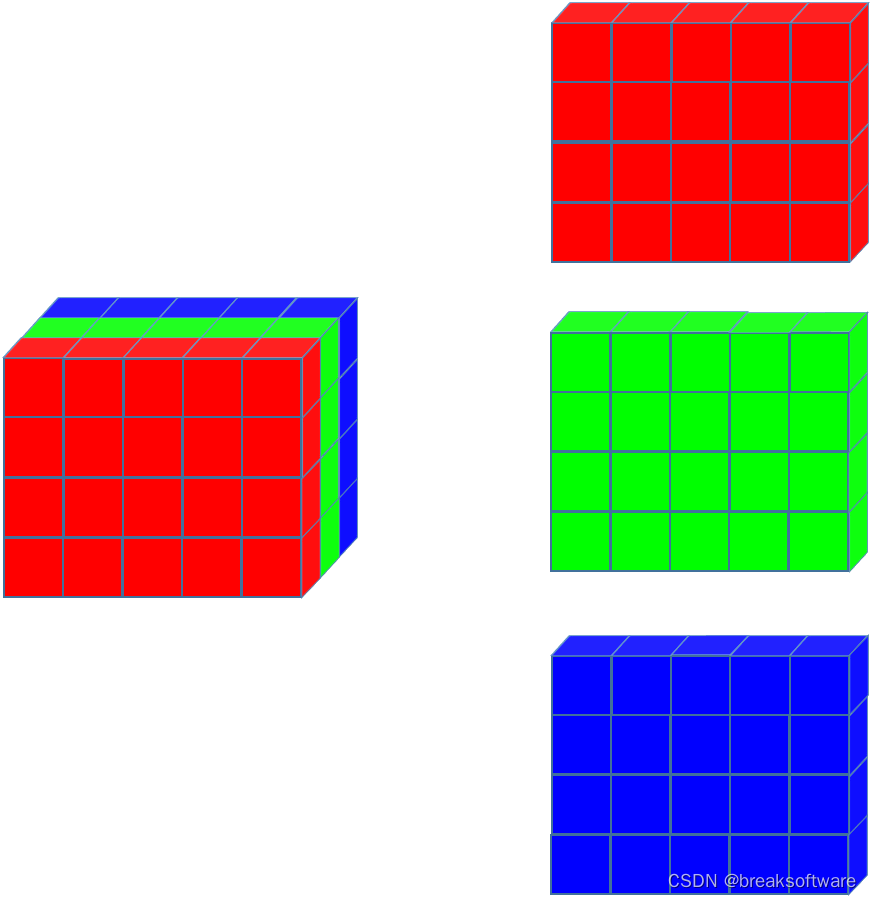
3维数组堆叠
我们构造出一个和上述只有一个原色的数组相同的数组,它们结构一致,但是每个元素的值为0。
zeros = np.zeros_like(blue)
然后使用dstack方法,将不同原色的三维数组进行堆叠。
redgreen = np.dstack((red, green, zeros))
redgreenImg = Image.fromarray(redgreen)
redgreenImg.save('redgreen.png')redblue = np.dstack((red, zeros, blue))
redblueImg = Image.fromarray(redblue)
redblueImg.save('redblue.png')greenblue = np.dstack((zeros, green, blue))
greenblueImg = Image.fromarray(greenblue)
greenblueImg.save('greenblue.png')
得出来的图如下



![[算法与数据结构][c++]:Static关键字和全局变量](https://img-blog.csdnimg.cn/img_convert/cbc3a1d31bdebf148e733f853d479674.png#pic_center)