初窥burnside

前言

• 最没道理的，竟做了一圈，菜的不成样子

Burnside

• 警告：我不会啊，只是一种理解罢了，符号，措辞，非常不严禁（欢迎大家指正）

\[|X/G|=\frac{1}{|G|}\sum_{g\in G}|X^g| \]

• \(X\) 表示所有方案的集合

• 若 \(x\in X,g\in G\) 有 \(x\cdot g=y\) 表示一种方案 \(x\) 在 \(g\) 变换后，变为一种方案 \(y\)

• \(X/G\) 表示，所有 \(G\) 作用在 \(X\) 后的等价类的集合，一个等价类，就是本质相同的一组方案，换句话说这组方案可以通过 \(G\) 中的变换，互相到达。

• \(X^g=\{x|x\cdot g=x,x\in X\}\)，在 \(g\) 变换后保持不变的。

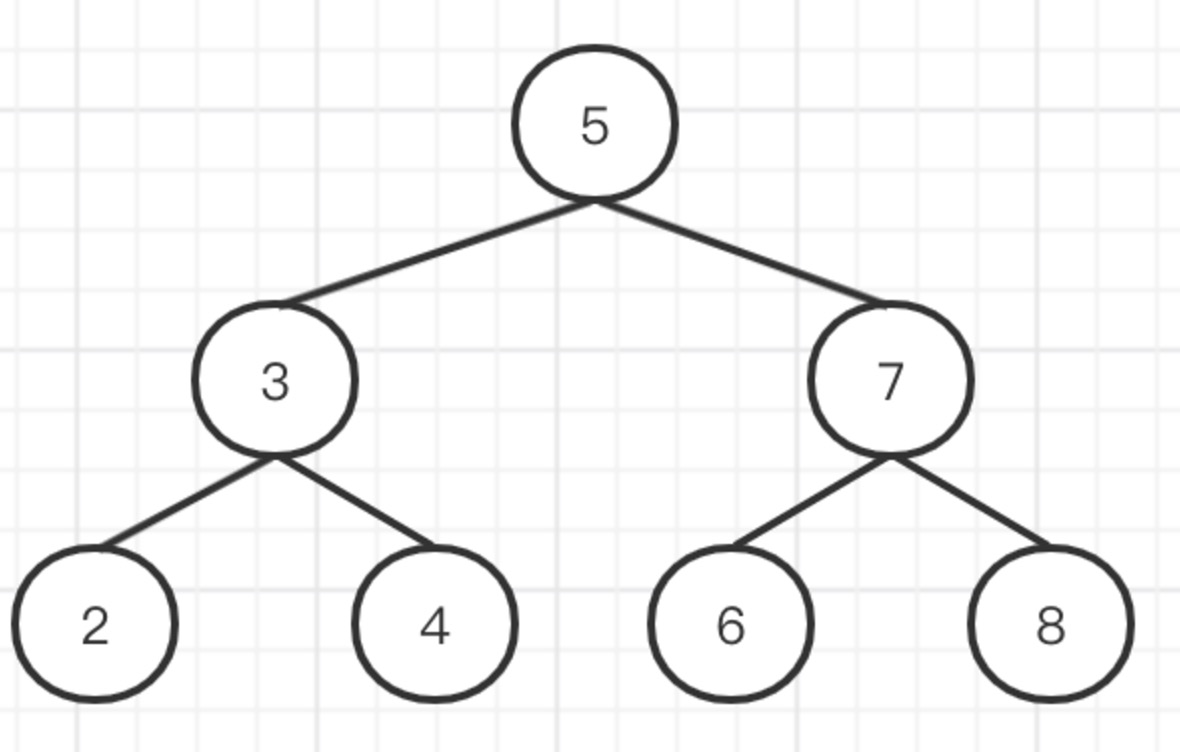
• 具体的，举例：长度为 \(4\) 的环 \(a_i\)，每个元素的取值为 \(A_0,A_1\)，计算本质不同的环的数量

• 给环标号为 \(1,2,3,4\)。

• \(X=\{\{A_0,A_0,A_0,A_0\},\{A_0,A_0,A_0,A_1\},\{A_0,A_0,A_1,A_0\},\{A_0,A_0,A_1,A_1\}\cdots,\{A_1,A_1,A_1,A_1\}\}\) 有 \(|X|=2^4\)

• \(G(\{g_0,g_1,g_2,g_3\},\cdot)\)

• \(g_0=(1,2,3,4)\)，\(g_1=(2,3,4,1)\)，\(g_2=(3,4,1,2)\)，\(g_3=(4,1,2,3)\)

• 我们定义 \(x\cdot g\) 为，举例说明 \(\{A_0,A_1,A_0,A_1\}\cdot g_1=\{A_1,A_0,A_1,A_0\}\)

• \(X^{g_2}=\{\{A_0,A_1,A_0,A_1\},\{A_0,A_0,A_0,A_0\},\{A_1,A_1,A_1,A_1\},\{A_1,A_0,A_1,A_0\}\}\)

• \(X/G=\{\{\{A_0,A_1,A_0,A_1\},\{A_1,A_0,A_1,A_0\}\},\{\{A_0,A_0,A_0,A_0\}\},\{\{A_0,A_1,A_1,A_0\},\{A_1,A_1,A_0,A_0\},\{A_1,A_0,A_0,A_1\},\{A_0,A_0,A_1,A_1\}\}\cdots\}\)

• 相信已经可以清楚的看到它们的结构了

• 算一下吧：\(ans=\frac{2^4+2^1+2^2+2^1}{4}=12\) 也不知道我算得对不对

题目描述

• [FJOI2007] 轮状病毒 的无标号版本，也就是旋转可以到达的算一种
• 使用 burnside 引理，明确有 \(n\) 个 \(g\)，顺时针旋转一个位置，两个位置，\(n\) 个位置
• 若我们考虑 \(g_k\) 求 \(|X^{g_k}|\) 我们分析，易得，我们需要有 \(\frac{n}{gcd(n,k)}\) 个长得完全一样的子树，大小为 \(gcd(n,k)\)，且这里的子树由于是 \(X\) 中的元素，故此有标号计数，就是原题轮状病毒。
• 设 \(F(d)\) 表示有标号计数，既大小为 \(d\) 时轮状病毒的答案。

\[ans=\frac{1}{n}\sum_{i=1}^nF(gcd(n,i))=\frac{1}{n}\sum_{d|n}F(d)(\sum_{i=1}^{\frac{n}{d}}[gcd(\frac{n}{d},i)=1])=\frac{1}{n}F(d)\varphi(\frac{n}{d}) \]

• \(F(d)\) 的求法，首先有简单的 \(n^2\) \(dp\)，轮状病毒的题解很全面了。

• 接着考虑用组和数刻画，具体的，我们要求的形式为 \(\sum\prod a_i\)，先求和让我们想到了插板法，后又乘积是不常见的形式。

• 我们先枚举段数，\(j\)，对于每一段我们有式子 \(F(d)=\sum_{j=1}^d2\binom{d+j}{2j}-\binom{d+j-1}{2j-1}\) 解释一下。我们想一下，统计一个环，我们给它加上 \(j\) 个板子。

• 而乘积，可以转化为在每一段中选择一个代表元素，于是就是 \(d+j\) 选 \(2j\) 个数，我们尝试构造，第一种我们把顺序第一个选的元素设为板子，第二个选择的元素为它上一个板子，下一个板子的代表元素，第3个选择的元素设为板子，依次类推，我们分配了一个环。第二种，我们先分配代表元素，后分配板子。

• 其实这里也有着一种巧合，就是有带表元素了，就正好不用管每一段大于等于 \(1\) 的限制了。但是这真对吗？只有一种情况会算重，就是在第一种中我们选择了第一个元素并设为了板子，和第二种中我们选择了最后一个元素并设为板子，这两个板子分得段其实是相同的，而我们多算了一遍所以减去。

• 减去的式子同样地道理，因为我们默认分割 \(1,n\) 两个元素，所以板子数量减 \(1\)，那我们第一个选择的元素必然为代表元素，之后是板子依次类推。

• 若您可以观察出来，\(F(d)=f_{2i}+f_{2i-2}-2\) 的话（\(f_0=f_1=1,f_{i+2}=f_{i}+f_{i+1}\)）就直接矩阵快速幂就行了。

• 可若是您没那么能观察，不妨考虑上面的有意思的组合计数方法，\(F(d)=\sum_{j=1}^d2\binom{d+j}{2j}-\binom{d+j-1}{2j-1}\)

• 我们直接把这里的思想运用到，\(dp\) 上，我们不枚举 \(j\) 了，然后交替放置板和代表元素。

• 我们设 \(dp_{i,1}\) 表示 \(i\) 之前结尾选的是代表元素，\(dp_{i,2}\) 表示 \(i\) 之前结尾玄德是板子

• 有初值 \(dp_{0,2}=1\) 有转移 \(dp_{i,1}=dp_{i-1,1}+dp_{i-1,2}\)，\(dp_{i,2}=dp_{i,1}+dp_{i-1,2}\)

• 最后 \(F(n)=2dp_{n,2}-dp_{n,1}-2\) 这里减的 \(2\) 是我们算初始值的时候，多的两个空板子。（亲测有效！！

• 最后只需构造 \(2\times 2\) 的矩阵即可。