一、正则化regularization

1.概念

正则化：减小方差的策略
什么叫误差？误差可分解为：偏差，方差与噪声之和。即误差 = 偏差 + 方差 + 噪声之和；
偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力
方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界

通过下面这幅图来理解上面三个差值概念：
这幅图是训练过程中，在训练集和验证集上面的损失曲线，红色的是在验证集上面的损失，橙色是在训练集上面的损失，我们在训练过程中希望损失越小越好；
偏差：我们训练集的损失大小，通常不考虑噪声的情况，也就是训练集与真实值之间的误差称为偏差；
方差：训练集与验证集之间的一个差异；
总结：我们的regularization就是为了解决方差过大的问题。

2.过拟合

下面这幅图训练的模型可以完整的拟合每一个训练集，但是无法拟合测试集，也就是我们说的过拟合现象，此时方差最大，regularization就是用来降低方差解决过拟合问题。

3.减小方差策略

在之前的博客文章讲过目标函数的公式，它是由代价函数和一个正则项组成，代价函数表示的是模型的输出与我们真实值之间的一个差异。而这个正则项则是为了约束我们模型的复杂度，让模型不那么复杂，常见的正则项有L1和L2

L1函数和L2函数分别表示下面的正方形和圆形，也就是正则项，彩色的圆盘表代表着cost，那么如何控制obj的值最小？先观察第一幅图片，当正方形的顶点和圆弧相交在w2轴的时候，obj最小；第二幅图，当两个圆相交，此时的点使得obj的值为最小。

4 正则化–权值衰减

L2 Regularization = weight decay（权值衰减）
我们习惯性把L2 Regularization正则项当作权值衰减，那么为什么要称L2为权值衰减呢，看一下下面公式；
下面是加上L2正则项之后求w梯度公式，直接看最后一步化简公式，我们通常取(0<λ<1)，所以w*(1-λ)该项是减小的，所以我们称L2正则项是权值衰减；

代码实现：
训练两个模型，带weight decay和不带weight decay的模型训练结果，权重衰减一般都放在优化器函数里面；

import torch  # 导入PyTorch库
import torch.nn as nn  # 导入PyTorch神经网络模块
import matplotlib.pyplot as plt  # 导入matplotlib用于绘图
import sys, os  # 导入系统和操作系统模块
hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")  # 获取项目路径
sys.path.append(hello_pytorch_DIR)  # 将项目路径添加到系统路径中from tools.common_tools import set_seed  # 导入自定义的公共函数
from torch.utils.tensorboard import SummaryWriter  # 导入PyTorch的TensorBoard可视化模块set_seed(1)  # 设置随机种子
n_hidden = 200  # 隐藏层神经元个数
max_iter = 2000  # 最大迭代次数
disp_interval = 500  # 显示间隔
lr_init = 0.01  # 初始学习率# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):  # 生成模拟数据函数w = 1.5  # 斜率train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)  # 生成训练数据xtrain_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())  # 生成训练数据ytest_x = torch.linspace(*x_range, num_data).unsqueeze_(1)  # 生成测试数据xtest_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())  # 生成测试数据yreturn train_x, train_y, test_x, test_y  # 返回训练数据和测试数据train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))  # 调用gen_data函数生成训练和测试数据# ============================ step 2/5 模型 ============================
class MLP(nn.Module):  # 定义多层感知器模型类def __init__(self, neural_num):  # 初始化函数super(MLP, self).__init__()self.linears = nn.Sequential(  # 多层感知器结构nn.Linear(1, neural_num),  # 全连接层nn.ReLU(inplace=True),  # ReLU激活函数nn.Linear(neural_num, neural_num),  # 全连接层nn.ReLU(inplace=True),  # ReLU激活函数nn.Linear(neural_num, neural_num),  # 全连接层nn.ReLU(inplace=True),  # ReLU激活函数nn.Linear(neural_num, 1),  # 全连接层)def forward(self, x):  # 前向传播return self.linears(x)  # 返回模型输出net_normal = MLP(neural_num=n_hidden)  # 创建无权重衰减的多层感知器模型
net_weight_decay = MLP(neural_num=n_hidden)  # 创建有权重衰减的多层感知器模型# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)  # 创建无权重衰减的优化器
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)  # 创建有权重衰减的优化器# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()  # 定义均方误差损失函数# ============================ step 5/5 迭代训练 ============================writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")  # 创建TensorBoard可视化对象
for epoch in range(max_iter):  # 迭代训练循环# forwardpred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)  # 分别计算无权重衰减和有权重衰减模型的预测值loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)  # 计算两种模型的损失值optim_normal.zero_grad()  # 清空无权重衰减优化器梯度optim_wdecay.zero_grad()  # 清空有权重衰减优化器梯度loss_normal.backward()  # 反向传播计算无权重衰减模型梯度loss_wdecay.backward()  # 反向传播计算有权重衰减模型梯度optim_normal.step()  # 更新无权重衰减模型参数optim_wdecay.step()  # 更新有权重衰减模型参数if (epoch+1) % disp_interval == 0:  # 每间隔disp_interval次迭代进行可视化和绘图# ==============================tensorboard可视化====================================for name, layer in net_normal.named_parameters():  # 添加无权重衰减模型梯度和参数直方图writer.add_histogram(name + '_grad_normal', layer.grad, epoch)writer.add_histogram(name + '_data_normal', layer, epoch)for name, layer in net_weight_decay.named_parameters():  # 添加有权重衰减模型梯度和参数直方图writer.add_histogram(name + '_grad_weight_decay', layer.grad, epoch)writer.add_histogram(name + '_data_weight_decay', layer, epoch)test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)  # 获取测试数据的预测值# ================================plt绘图==============================================plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')  # 绘制训练数据散点图plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')  # 绘制测试数据散点图plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')  # 绘制无权重衰减模型预测曲线plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')  # 绘制有权重衰减模型预测曲线plt.text(-0.25, -1.5, 'no weight decay loss={:.6f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})  # 显示无权重衰减模型损失值plt.text(-0.25, -2, 'weight decay loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})  # 显示有权重衰减模型损失值plt.ylim((-2.5, 2.5))  # 设置y轴范围plt.legend(loc='upper left')  # 设置图例位置plt.title("Epoch: {}".format(epoch+1))  # 设置图标题plt.show()  # 展示图plt.close()  # 关闭图

plt绘制结果：
在训练到第2000轮的时候，无权值衰减的红色曲线虽然在训练集上表现非常好Loss为0，但是产生了严重的过拟合，在测试集上面表现非常差，此时的方差最大，

tensorboard展示：
不带有权值衰减方法的网络层，随着训练次数的增加，权重没有发生变化，但是带有权值初始化的网络，随着训练的加深，网络的权重也在降低，最后控制在[-0.25,0.25]之间。

权值下降原理
在优化器更新这行打上断点，进入debug模型，进入到SGD优化器函数当中；

找到权重衰减实现公式：
该行代码表示d_p=d_p+param*alpha，d_p表示的就是求导；

二、正则化-dropout

2.1 dropout概念

    Dropout是一种用于深度学习模型的正则化技术。正则化旨在防止模型过度拟合训练数据，提高模型的泛化能力。Dropout的基本思想是在训练期间随机“丢弃”（即将其权重设置为零）神经网络中的一些单元，从而减少神经网络的复杂度，防止过拟合。
    具体来说，Dropout在训练期间随机选择一些神经元，并将它们的输出设置为零。这样，每个神经元都不能依赖于特定的其他神经元，因为任何神经元在任何时刻都有可能被“丢弃”。这迫使网络中的每个神经元都变得更加独立，减少了神经元之间的复杂依赖关系。
    在实践中，Dropout通常通过在训练期间以一定的概率（通常在0.2到0.5之间）随机将神经元的输出置为零来实现。在测试期间，所有神经元都保持激活。这是因为在测试时，我们希望使用整个模型进行预测，而不是随机地“关闭”一些神经元。
    Dropout的优势在于它能够显著减少过拟合，提高模型的泛化性能。这种技术已经被广泛应用于深度学习中的各种任务，如图像分类、自然语言处理等。

下面这幅图分别是正常神经元连接，和神经元随机失活，随机失活之后神经元的weight=0；

2.2 数据尺度变化

测试时，所有权重乘以1-drop_prob，为什么要做这样的一个变化？
例如：drop_prob = 0.3 ， 1-drop_prob = 0.7，我们有100个神经元，在训练过程中随机失活30%，那么实际训练过程中是有70个事有权重的，所以训练过程中的数据尺度是70，但是在测试过程中所有神经元都存在，此时的数据尺度为100，那么训练过程中和测试过程中的数据尺度会存在差异，这会导致我们模型的精度产生差异，所以在测试过程中，需要对所有的权值乘以0.7，也就是1-drop_prob，这样可以保证数据尺度一致。

2.3 nn.Dropout

功能：Dropou t层
参数：
• p：被舍弃概率，失活概率

pytorch实现细节：
这样做的好处，在训练的时候增加神经元权值，在测试阶段不需要做任何处理。

代码实现：

# -*- coding:utf-8 -*-  # 定义编码格式为utf-8import torch  # 导入PyTorch库，一个开源的神经网络库
import torch.nn as nn  # 导入PyTorch的神经网络模块
import matplotlib.pyplot as plt  # 导入Matplotlib库，用于绘图
import sys, os  # 导入系统模块和os库hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__) + os.path.sep + ".." + os.path.sep + "..")  # 获取当前文件所在的目录的上一级目录的上一级目录的绝对路径，通常用于指定路径
sys.path.append(hello_pytorch_DIR)  # 将该路径添加到Python的系统路径中，使得可以导入该路径下的模块from tools.common_tools import set_seed  # 导入common_tools模块中的set_seed函数，用于设置随机种子
from torch.utils.tensorboard import SummaryWriter  # 导入TensorBoard模块中的SummaryWriter类，用于写入tensorboard的日志set_seed(1)  # 设置随机种子为1，为了使结果可复现
n_hidden = 200  # 定义隐藏层单元数量为200
max_iter = 2000  # 最大迭代次数为2000次
disp_interval = 500  # 每隔disp_interval轮迭代显示一次信息
lr_init = 0.01  # 初始学习率为0.01# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):  # 定义一个函数，用于生成数据，num_data表示生成数据的数量，x_range表示数据范围w = 1.5  # 定义权重wtrain_x = torch.linspace(*x_range, num_data).unsqueeze_(1)  # 生成训练数据x，使用linspace生成等间距的数据，unsqueeze_将数据形状扩展为[样本数, 特征]的形式train_y = w * train_x + torch.normal(0, 0.5, size=train_x.size())  # 根据训练数据x和权重w生成对应的y值，并添加高斯噪声test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)  # 生成测试数据xtest_y = w * test_x + torch.normal(0, 0.3, size=test_x.size())  # 根据测试数据x和权重w生成对应的y值，并添加更小的噪声return train_x, train_y, test_x, test_y  # 返回训练数据、标签，测试数据、标签train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))  # 在这里调用gen_data函数生成数据，范围为(-1,1)# ============================ step 2/5 模型 ============================
class MLP(nn.Module):  # 定义一个神经网络模型MLP，继承自PyTorch的nn.Module类def __init__(self, neural_num, d_prob=0.5):  # 在初始化函数中定义模型的结构，neural_num表示神经元的数量，d_prob表示dropout的概率super(MLP, self).__init__()  # 调用父类的初始化函数self.linears = nn.Sequential(  # 定义一个序列模型，包含多个线性层和ReLU激活函数nn.Linear(1, neural_num),  # 第一层线性层，输入为1维，输出为neural_num维nn.ReLU(inplace=True),  # 添加ReLU激活函数，inplace=True表示原地操作，即不创建额外的内存空间nn.Dropout(d_prob),  # 应用d_prob概率的dropout层，对每个样本的特征进行随机失活（即不传递）一部分特征nn.Linear(neural_num, neural_num),  # 第二层线性层，输入为neural_num维，输出为neural_num维nn.ReLU(inplace=True),  # 添加ReLUnn.Dropout(d_prob),nn.Linear(neural_num, neural_num),nn.ReLU(inplace=True),nn.Dropout(d_prob),nn.Linear(neural_num, 1),)def forward(self, x):return self.linears(x)net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.)
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_prob_0.parameters(), lr=lr_init, momentum=0.9)
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()# ============================ step 5/5 迭代训练 ============================writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):pred_normal, pred_wdecay = net_prob_0(train_x), net_prob_05(train_x)loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)optim_normal.zero_grad()optim_reglar.zero_grad()loss_normal.backward()loss_wdecay.backward()optim_normal.step()optim_reglar.step()if (epoch + 1) % disp_interval == 0:net_prob_0.eval() #测试阶段一定要设置eval模式net_prob_05.eval()# 可视化for name, layer in net_prob_0.named_parameters():writer.add_histogram(name + '_grad_normal', layer.grad, epoch)writer.add_histogram(name + '_data_normal', layer, epoch)for name, layer in net_prob_05.named_parameters():writer.add_histogram(name + '_grad_regularization', layer.grad, epoch)writer.add_histogram(name + '_data_regularization', layer, epoch)test_pred_prob_0, test_pred_prob_05 = net_prob_0(test_x), net_prob_05(test_x)# 绘图plt.clf()plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')plt.plot(test_x.data.numpy(), test_pred_prob_0.data.numpy(), 'r-', lw=3, label='d_prob_0')plt.plot(test_x.data.numpy(), test_pred_prob_05.data.numpy(), 'b--', lw=3, label='d_prob_05')plt.text(-0.25, -1.5, 'd_prob_0 loss={:.8f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})plt.text(-0.25, -2, 'd_prob_05 loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})plt.ylim((-2.5, 2.5))plt.legend(loc='upper left')plt.title("Epoch: {}".format(epoch + 1))plt.savefig('image_{}.png'.format(epoch + 1))plt.show()plt.close()net_prob_0.train()net_prob_05.train()

plt绘图展示
训练2000轮之后，发现虽然不带dropout的模型可以很好的拟合训练集，但是在测试集上面的拟合效果很差，出现了严重的过拟合现象，但是带有dropout的网络不会出现过拟合现象。

tensorboard展示
不带dropout的线性层，随着训练轮数的叠加，权值没有发生太多的变换，但是带有dropout的线性层，随着训练轮数的叠加，权值在不断减小。

2.4 两种模式

在神经网络的训练过程中，PyTorch提供了两种模型状态：eval()模式和train()模式。

1. train()模式：
   在神经网络训练阶段，通常使用train()模式。在这种模式下，神经网络会保留所有的层和参数，并对输入进行高效地求导和反向传播，以便进行参数的更新。此外，训练模式还会启用Dropout层和Batch Normalization层，以便在每一次前向传播和反向传播中对数据进行随机失活和归一化处理，从而提高模型的泛化能力和训练效果。

2. eval()模式：
   在神经网络测试和验证阶段，通常使用eval()模式。在这种模式下，神经网络会关闭Dropout层和Batch Normalization层的随机失活和归一化处理，以便保持模型的稳定性和一致性。此外，eval()模式还会关闭自动求导机制，减少了内存占用和提高了前向传播的速度，使得模型的性能更加高效。

总之，train()模式主要用于训练神经网络，包括前向传播、反向传播和参数更新；eval()模式主要用于测试和验证神经网络，包括前向传播和模型预测。在实际使用中，通过在不同阶段使用不同的模式，可以更好地控制神经网络的行为，从而获得更好的训练和测试效果。

三、Batch Normalization

参考文献：《Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift》

3.1 ICS现象（Internal Covariate Shift，内部协变量偏移)

BN的提出最开始是要解决ICS现象，那么什么是ICS现象呢？从下面这幅图理解，我们神经网络是累乘的形式，当中间的乘积出现增加或者减少的情况，会导致梯度爆炸或者梯度消失的现象。

ICS现象：输入数据分布变化，导致的模型训练困难，对深度神经网络影响极大

模型训练过程中，中间隐藏层每次训练输入神经元的数据分布发生变化，从而导致训练困难

内部协变量偏移（Internal Covariate Shift）是深度学习中一个常见的问题。它指的是在神经网络的训练过程中，网络的每一层输入分布的变化导致模型难以训练的情况。这种现象通常在深度神经网络的训练中出现，尤其是在使用批量归一化（Batch Normalization）等技术之前。

具体来说，神经网络的每一层在训练过程中都会接收前一层的输出作为输入，而这个输入的分布会随着网络参数的更新而变化。如果每一层的输入分布发生变化，那么每一层都需要不断适应新的分布，这会使得训练变得更加困难。

内部协变量偏移的影响包括：

1. 训练收敛缓慢： 由于每一层都需要适应新的输入分布，模型的训练可能会收敛得相对较慢。
2. 需要更小的学习率： 为了应对输入分布的变化，通常需要减小学习率，以确保模型的权重能够适应新的数据分布。
3. 可能导致梯度爆炸或梯度消失： 输入分布的变化可能导致梯度在网络中传播时出现梯度爆炸或梯度消失的问题。

批量归一化是一种用于缓解内部协变量偏移的技术。它通过在每一层的输入上进行归一化，使得每层的输入分布保持稳定，有助于更快的训练收敛。

总体而言，理解和处理内部协变量偏移是深度学习中非常重要的一部分，以提高模型的训练效果和泛化能力。

3.2 BN原理

计算公式：
首先计算mini-batch的平均值，再计算方差，然进行normalize，完成0均值，1标准差，最后再进行affine transform缩放和位移；

批：一批数据，通常为mini-batch
标准化：使得分布为 mean=0， std=1

例如：如 1， 2 ；mean=1.5， std=0.5， 变换得到-1， 1 一定有正有负，并且拉到0附近了

bn层计算原理：一个网络中有多个网络层，假设batch设置为2，此时对于两个网络中同一个网络层同一个位置的神经元进行bn计算，如下图：

并不是对同一个网络层中所有的神经元进行bn计算，而且按照下方红色方框中不同批次同一维度进行计算。

3.3 BN的优点

优点：

1. 可以用更大学习率，加速模型收敛，如果学习率过大，会导致梯度的递增，从而导致模型无法训练，使用BN之后可以使用较大的学习率，从而加速学习率的收敛；
2. 可以不用精心设计权值初始化：因为数据的尺度可能会逐渐的变大或者变小，从而导致梯度激增或者减小，使用BN可以规范我们的数据尺度；
3. 可以不用dropout或较小的dropout：在实验过程中得到的结果；
4. 可以不用L2或者较小的weight decay：实验所得；
5. 可以不用LRN(local response normalization)：对数据尺度进行规范

3.4 数据尺度实验

设置bn层的数据尺度变化：

class MLP(nn.Module):def __init__(self, neural_num, layers=100):super(MLP, self).__init__()self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])self.neural_num = neural_numdef forward(self, x):for (i, linear), bn in zip(enumerate(self.linears), self.bns):x = linear(x)x = bn(x)  # 设置bnx = torch.relu(x)if torch.isnan(x.std()):print("output is nan in {} layers".format(i))breakprint("layers:{}, std:{}".format(i, x.std().item()))return x

输出结果：

不设置bn层数据尺度，在forward中注释掉bn方法，数据尺度会随着网络层数增加，逐渐变小：

完整代码：

# -*- coding: utf-8 -*-import torch
import numpy as np
import torch.nn as nnimport sys, oshello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__) + os.path.sep + ".." + os.path.sep + "..")
sys.path.append(hello_pytorch_DIR)from tools.common_tools import set_seedset_seed(1)  # 设置随机种子class MLP(nn.Module):def __init__(self, neural_num, layers=100):super(MLP, self).__init__()self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])self.neural_num = neural_numdef forward(self, x):for (i, linear), bn in zip(enumerate(self.linears), self.bns):x = linear(x)# x = bn(x)  # 设置bnx = torch.relu(x)if torch.isnan(x.std()):print("output is nan in {} layers".format(i))breakprint("layers:{}, std:{}".format(i, x.std().item()))return xdef initialize(self):for m in self.modules():if isinstance(m, nn.Linear):# method 1# nn.init.normal_(m.weight.data, std=1)    # normal: mean=0, std=1# method 2 kaimingnn.init.kaiming_normal_(m.weight.data)neural_nums = 256
layer_nums = 100
batch_size = 16net = MLP(neural_nums, layer_nums)
# net.initialize()inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1output = net(inputs)
print(output)

3.5 实际模型训练

1、以人民币二分类实验为例
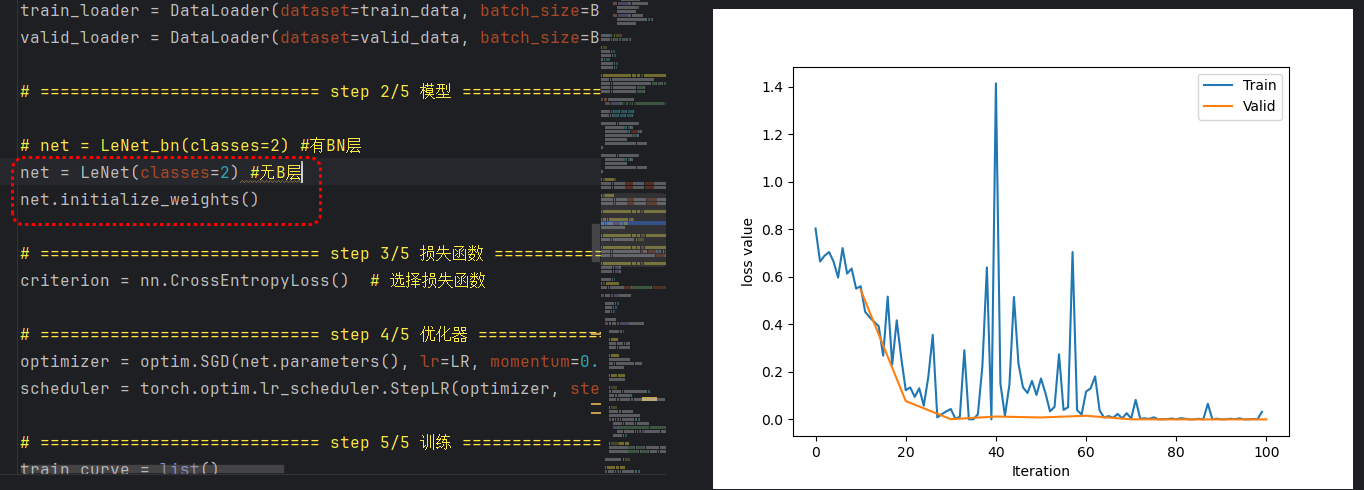
不设置权值初始化和BN层，会发现训练过程中损失波动很大：

2、设置权值初始化，不设置bn层，虽然也会有波动，但是最后依旧可以收敛。

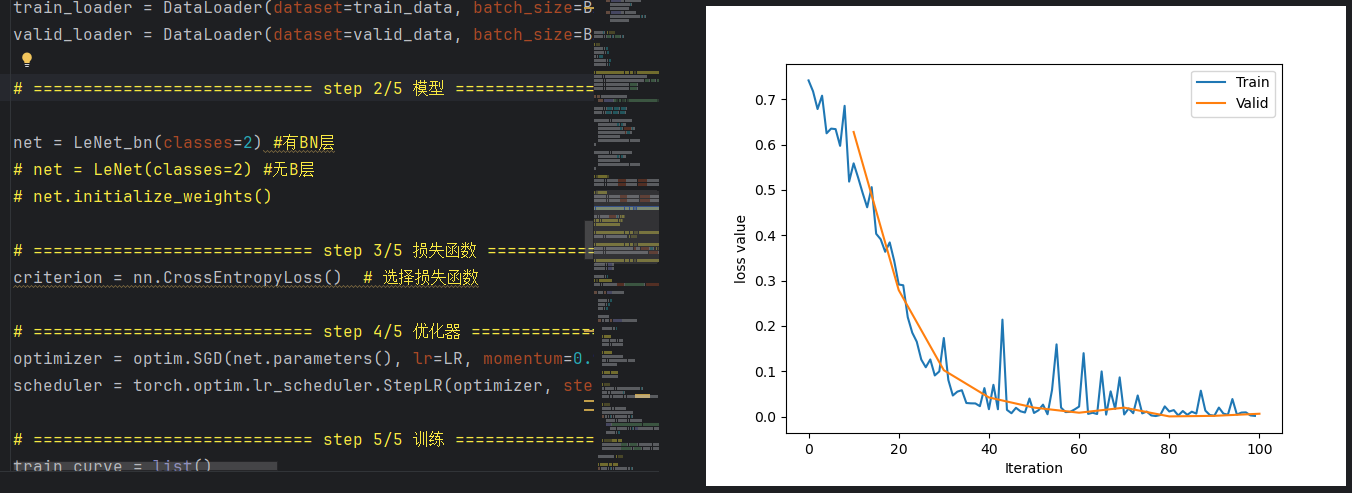
3、设置BN层，不设置权值初始化，训练过程中损失波动非常小，并且可以收敛。

3.6 _BatchNorm

3.6.1 相关参数分析

• nn.BatchNorm1d
• nn.BatchNorm2d
• nn.BatchNorm3d
参数：
• num_features：一个样本特征数量（最重要）；
• eps：分母修正项，通常会设置一个非常小的数，避免分母为0；
• momentum：指数加权平均估计当前mean/var，通常设置为0.1；
• affine：是否需要affine transform，默认为True；
• track_running_stats：是训练状态，还是测试状态，训练状态的话均值和方差需要重新估计，测试状态则是采用当前的均值和方差；

---

主要属性：
• running_mean：均值
• running_var：方差
• weight：affine transform中的gamma
• bias： affine transform中的beta

注意：均值、方差采用指数加权平均计算得来，测试时候采用当前统计值；
running_mean = (1 - momentum) * pre_running_mean + momentum * mean_t
running_var = (1 - momentum) * pre_running_var + momentum * var_t
weight、bias是在模型训练过程中计算出来的，会发生变化；

3.6.2 1d、2d、3d特征区别

1d：输出输入形式是batch_sizex特征数x特征维度=3x5x1
2d：输入形式是3x3x(2x2)，一个特征图的shape是2x2
3d：输入形式是3x3x(2x2x3)
我们计算均值和方差都是在不同batch同一维度上进行计算，也就是红色虚线框当中的所有数据。

3.6.3 1d代码实现

flag = 1
# flag = 0
if flag:batch_size = 3  # 批大小num_features = 5  # 特征数量momentum = 0.3  # 动量features_shape = (1)  # 一个黄色框，表示一个特征图feature_map = torch.ones(features_shape)  # 1Dfeature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)  # 2Dfeature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)  # 3Dprint("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))  # 打印输入数据及其形状bn = nn.BatchNorm1d(num_features=num_features, momentum=momentum)  # 创建BatchNorm1d层对象running_mean, running_var = 0, 1  # 运行时均值和方差初始化for i in range(2):  # 循环迭代两次outputs = bn(feature_maps_bs)  # BatchNorm1d前向传播print("\niteration:{}, running mean: {} ".format(i, bn.running_mean))  # 打印运行时均值print("iteration:{}, running var:{} ".format(i, bn.running_var))  # 打印运行时方差mean_t, var_t = 2, 0  # 设定均值和方差running_mean = (1 - momentum) * running_mean + momentum * mean_t  # 更新运行时均值running_var = (1 - momentum) * running_var + momentum * var_t  # 更新运行时方差print("iteration:{}, 第二个特征的running mean: {} ".format(i, running_mean))  # 打印更新后的运行时均值print("iteration:{}, 第二个特征的running var:{}".format(i, running_var))  # 打印更新后的运行时方差

输出结果：

分析：
我们第一个维度所有特征都为1，按照正常计算方法应该均值为1，但是为什么计算会得到0.3，因为我们加了一个momentum动量，我们看一下running_mean计算公式如下，running_mean等于当前的均值x动量+上一层均值x(1-动量)，因为上一层没有数据，所以均值设置为0，所以running_mean=0.3x1=0.3；

3.6.4 2d代码实现

# ======================================== nn.BatchNorm2d
flag = 1
# flag = 0
if flag:batch_size = 3  # 批大小num_features = 3  # 特征数量momentum = 0.3  # 动量features_shape = (2, 2)  # 特征图形状feature_map = torch.ones(features_shape)  # 2Dfeature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)  # 3Dfeature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)  # 4Dprint("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))  # 打印输入数据及其形状bn = nn.BatchNorm2d(num_features=num_features, momentum=momentum)  # 创建BatchNorm2d层对象running_mean, running_var = 0, 1  # 运行时均值和方差初始化for i in range(2):  # 循环迭代两次outputs = bn(feature_maps_bs)  # BatchNorm2d前向传播print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape))  # 打印运行时均值的形状print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape))  # 打印运行时方差的形状print("iter:{}, weight.shape: {}".format(i, bn.weight.shape))  # 打印权重的形状print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))  # 打印偏置的形状

输出结果：

---