模型评估：ROC曲线-编程知识

二值分类器（Binary Classifier）是机器学习领域中最常见也是应用最广泛的分类器。评价二值分类器的指标很多，比如precision、recall、F1 score、P-R曲线等。相比而言，ROC曲线有很多优点，经常作为评估而知分类器最重要的指标之一。下面我们来详细了解一下ROC曲线的绘制方法和特点。

1. 什么是ROC曲线？

ROC曲线是Receiver Operating Characteristic Curve 的简称，中文名为“受试者工作特征曲线”。ROC曲线源于军事领域，而后在医学领域应用甚广，“受试者工作特征曲线”这一名称也正是来自于医学领域。

ROC曲线的横坐标为假阳性率（False Positive Rate, FPR）；纵坐标为真阳性率（True Positive Rate, TPR）。FPR和TPR的计算方法分别为

$FPR=\frac{FP}{N}$

$TPR=\frac{TP}{P}$

上式中，P是真正的正样本的数量，N是真实的负样本数量，TP是P个正样本中被分类器预测为正样本的个数，FP是N个负样本中被分类器预测为正样本的个数。

为了更直观地说明这个问题，我们举一个医院诊断病人的例子。假设有10为意思癌症患者，其中有3位很不幸确实患了癌症（P=3），另外7位不是癌症患者（N=7）。医院对这10位疑似患者做了诊断，判断出3位癌症患者，其中有2位确实是真正的患者（TP=2）。那么真阳性率TPR=TP/P=2/3. 对于7为非癌症的患者来说，有一位很不幸被误诊为癌症患者（FP=1），那么假阳性率FPR=FP/N=1/7. 对于“该医院”这个分类器来说，这组分类结果就对应ROC曲线上的一个点（1/7,2/3）。

2.如何绘制ROC曲线？

事实上，ROC曲线是通过不断移动分类器的“截断点”来生成曲线上的一组关键点的，通过下面的例子进一步来解释“截断点”的概念。

在二值分类问题中，模型的输出一般都是预测样本为正例的概率。假设测试集中有20个样本，表2.1是模型的输出结果。样本按照预测概率从高到低排序。在输出最终的正例、负例之前，我们需要指定一个阈值，预测概率大于该阈值的样本会被判为正例，其他的全部都是负例。上面所说的“截断点”指的就是区分正负预测结果的阈值。

通过动态地调整截断点，从最高的得分开始（实际上是从正无穷开始，对应着ROC曲线的零点），逐渐调整到最低得分，每一个截断点都会对应一个FPR和TPR，在ROC图上绘制出每个截断点对应的位置，再连接所有点就得到最终的ROC曲线。

就此例来说，当截断点选择为正无穷时，模型把全部样本预测为负例，那么FP和TP必然都为0，FPR和TPR也都为0，因此曲线的第一个点的坐标就是（0,0）。当把截断点调整为0.9时，模型预测1号样本为正样本，并且该样本确实是正样本，因此，TP=1, 20个样本中，所有正例数量为P=10，故TPR=TP/P=1/10, 负样本总数N=10，故FPR=FP/N=0/10=0，对应ROC曲线上的点（0,0.1）。依次调整截断点，直到画出全部的关键点，再连接关键点即得到最终的ROC曲线，如图2.2所示。

其实，还有一种更直观地绘制ROC曲线的方法。首先，根据样本标签统计出正负样本的数量，假设正样本数量为P，负样本数量为N；接下来，把横轴的刻度间隔设置为1/N，纵轴的刻度间隔设置为1/P；再根据模型输出的预测概率对样本进行排序（从高到低）；依次遍历样本，同时从零点开始绘制ROC曲线，每遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线，每遇到一个负样本就沿横轴方向绘制一个刻度间隔的曲线，直到遍历完所有样本，曲线最终停在（1,1）这个点，整个ROC曲线绘制完成。

3.如何计算AUC?

AUC指的是ROC曲线下的面积大小，该值能够量化地反映基于ROC曲线衡量出的模型性能。计算AUC值只需要沿着ROC横轴做dx积分就可以了。由于ROC曲线一般都处于y=x这条直线的上方（如果不是的话，只要把模型预测的概率反转成1-p就可以得到一个更好的分类器），所以AUC的取值一般在0.5-1之间。AUC越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。

4.ROC曲线相比P-R曲线有什么特点？

当正负样本的分布发生变化时，ROC曲线的形状能够基本保持不变，而P-R曲线的形状一般会发生较剧烈的变化。

举例来说，图2.3是ROC曲线和P-R曲线的对比图，其中图2.3（a）和图2.3（c）是ROC曲线，图2.3（b）和图2.3（d）是P-R曲线，图2.3（c）和图2.3（d）则是将测试集中的负样本数量增加10倍之后的曲线图。

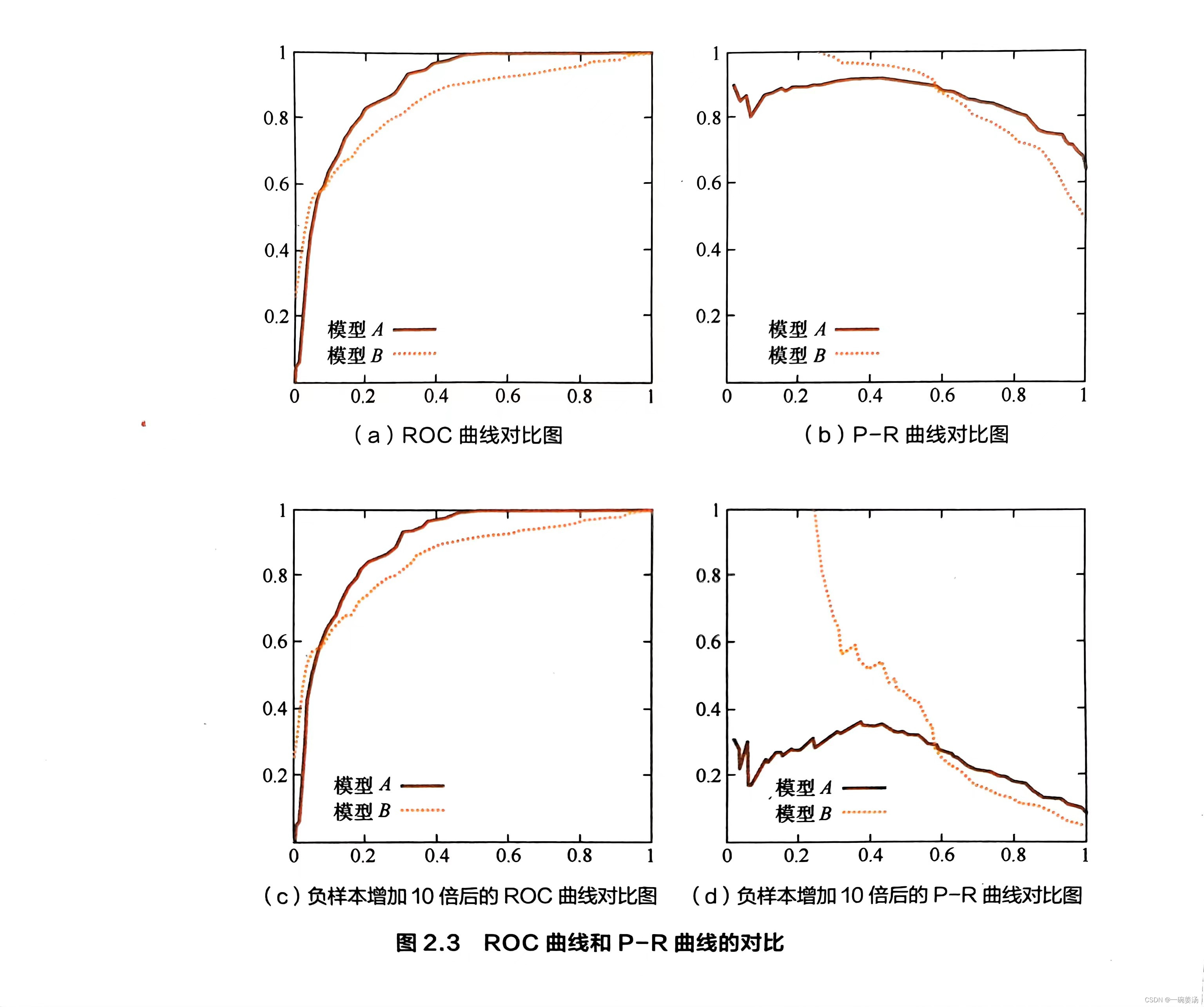
可以看出，P-R曲线发生了明显的变化，而ROC曲线形状基本不变。这个特点让ROC曲线能够尽量降低不同测试集带来的干扰，更加客观地衡量模型本身的性能。这有什么实际意义呢？在很多实际问题中，正负样本数量往往很不均衡。比如，计算广告领域经常涉及转化率模型，正样本的数量往往是负样本数量的1/1000甚至是1/10000. 若选择不同的测试集，P-R曲线的变化就会非常大，而ROC曲线则能够更加稳定地反映模型本身的好坏。所以，ROC曲线的适用场景更多，被广泛用于排序、推荐、广告等领域。但需要注意的是，选择P-R曲线还是ROC曲线是因实际问题而异的，如果研究者希望更多地看到模型在特定数据集上的表现，P-R曲线则能够更直观地反映其性能。