理解Herbrand Equivalence-编程知识

笔者最近在看GVN的一系列论文，总会看到一个概念叫Herbran Equivalence，依靠这种定义，能够判断一个GVN算法是否是complete的，也即检测一个算法是否是precise的，只有找到所有Herbrand Equivalence关系的算法才能称得上是完全的。

理解：程序表达式之间的等值关系是不可判定的

由于检测程序表达式间一般的等值关系是不可判定的，大部分ＧＶＮ算法都将问题做了简化，通常假设条件语句的结果在编译期间是不确定的，并且对所有的运算符都不考虑其特殊语义，即忽略它们可能满足的特殊运算法则，将不同结构的表达式看作不同的表达式．满足这些限制条件的表达式间的等值关系被称作 Herbrand 等值关系.能够检测到程序中全部 Herbrand 等值关系的ＧＶＮ算法被称为完全ＧＶＮ算法.
以上内容摘自《一种高效的完全值编号算法》。
两个程序表达式是否是等值的，这个问题在编译是无法判定，例如表达式a + b 和 a * b，表面看起来二者不是相等的，但是当运行时赋值a = 2, b = 2，此时两个表达式就是相等的。假定条件表达式在编译期不确定，前提是条件表达式的值不能通过静态分析得到，也即phi结点的两个分支执行哪个是不确定的。所有的运算符不考虑特殊语义，结合下文是说不考虑两个不同运算结构之间的等价性。

phi结点和普通表达式之间的相等性

这篇论文中还举了一些算法之所以是不完全的例子——也即他们无法发现phi结点和普通表达式之间的相等性。
以下几个例子实现了论文中的几个例子。
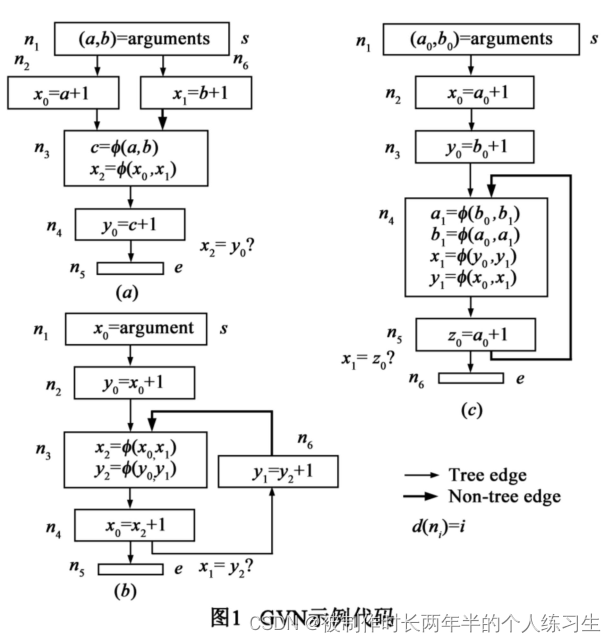
在这里插入图片描述

例子1：在input例子中发现两个表达式x和y的相等性，在LLVM 中可以识别到此两个表达式之间的相似性并删除之。贴一个Compiler Explorer的链接。

#include <stdio.h>int input(int a, int b) {int c, d, e, x, y, z;scanf("%d", &d);if(d) {x = a + 1;c = a;} else {x = b + 1;c = b;}y = c + 1;scanf("%d", &e);if(e) {return x;} else {return y;}
}int main()
{int a, b;scanf("%d %d", &a, &b);input(a, b);
}

生成的IR主要部分如下：

  %0 = load i32, ptr %d, align 4%tobool.not = icmp eq i32 %0, 0%b.a = select i1 %tobool.not, i32 %b, i32 %a%retval.0 = add nsw i32 %b.a, 1ret i32 %retval.0

突然发现，论文给出了例子2是有问题的。
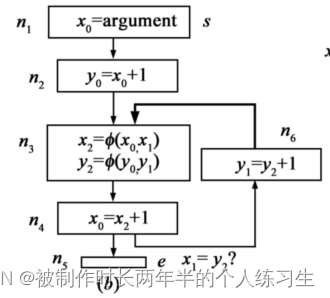
在这里插入图片描述
这里使用的标记方法是先将 $\phi$ 结点的所有分支标记完再标记 $\phi$ 结点，这本身并没有问题，问题在于 $n_4$ 中的表达式应该为 $x_1 = x_2 + 1$ 。
在修改之后的情况下，当 $n_4$ 基本块的结尾到 $n_5$ 基本块或是 $n_4$ 基本块的结尾到 $n_3$ 基本块的开始都是满足 $x_1=y_2$ 的情况的，但是在 $n_3$ 到 $n_4$ 结尾这部分是不满足上述等值关系的。因此此种情况可以将两者标记为等值表达式但需要注意范围，不能贸然消除。
例子2对应的Compiler Explorer链接。
例子2：

#include <stdio.h>
int z;
int input(int x, int e, int f) {int y;y = x + 1;do {// if (x == y) {//     z = 1;// } else {//     z = 0;// }x++;// if (x == y) {//     z = 1;// } else {//     z = 0;// }if (e++ > 0) {break;} else {y++;}} while (1);return 0;
}int main() {int x, e, f;scanf("%d %d %d", &x, &e, &f);return input(x, e, f);
}

为了尽量凸显对该GVN能否正确识别，我修改了原文的例子以更好的阐述笔者的思想，读者可以自己尝试，当第一处注释打开时，编译器会判定两个表达式不相等，因此将全局变量z设置为0，第二处注释打开时，编译器会判定两个表达式相等，将全局变量设置为1.对应上图中x1和y1不相等，但x1和y2相等。

第三个例子不能用LLVM实现，因为LLVM不存在两个phi结点的依赖关系。也即图中 $a_1$ 和 $b_1$ 之间存在着矛盾关系。
根据论文后续的描述也说明了上述例子在SSA中不成立。相关描述如下：

本文中的模型和算法都基于静态单赋值形式的程序．在一个静态单赋值形式的程序中，所有变量都有唯一的定值语句，并且所有对变量的使用都被该变量的定值语句所支配，即从程序的入口到达对该变量的使用的所有执行路径都一定经过该变量的定值语句．

可以看到，在上述例子中b1的第一次使用并没有经过其定值。

《一种高效的完全值编号算法》定义的值编号

论文的第二和第三部分分别给出了Herbrand等值关系和值编号的定义。

定义Herbrand等值关系

首先来看第二部分。
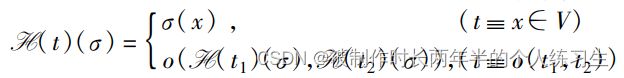
在这里插入图片描述
此公式首先定义了某个值到一个表达式的定义，作者的思路是将所有的值都上溯到定义他们的表达式的形式，这样可以比较不同值之间的相等性，带着这样的想法再来看上述公式，第一种情况是t=x的形式（根据后文的描述称为变量表达式），直接将x的表达式传递给t，第二种是t = t1 o t2的二元表达式形式（根据后文的描述称为包含运算符的表达式），将两个二元表达式的操作数的定义进行二元计算。
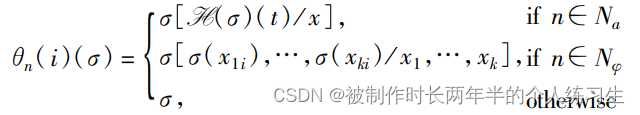
在这里插入图片描述
其后作者又定义了一个转换函数，也即经过一个程序节点（语句）之后表达式集合的变化，第一种可能是赋值语句，直接将表达式中的t换成x。如果是phi结点，将每条分支上的都进行转换。

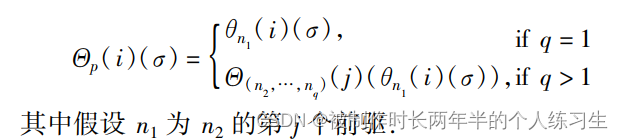
有了单个节点的处理方式，就能够得到一条路径的处理方式，无外乎将不同节点之间的转换函数连接，当遇到phi节点时，当路径明确的情况下也就能选择出某个分支。
在这里插入图片描述
基于上述公式给出了一个P-Herbrand关系，这里的P是Partial的简写，突出了当前路径只是一种可能的运行情况。这个公式定义的不清晰，根据下文的描述应该是检测了某个路径下的Herbrand等值关系。
最后一句话是说当P是所有路径的集合时，得到的Herbrand等值关系不再是部分的，所以可以省略前缀P-。

定义值编号

值编号定义前，作者先定义了两个值编号之间的比较，有如下公式。
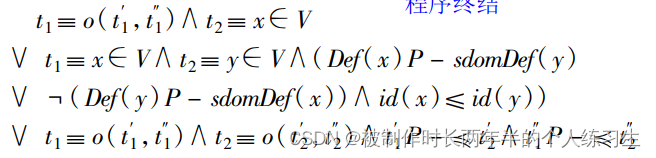
在这里插入图片描述
集合原文的描述更容易理解，这里我只说一个问题，第三行两个表达式写反了，应该是第二行最后一部分的否定，否则第二行和第三行不能构成一个分支上的完备集。

上述定义很明显，如果有变量表达式，那么从其等值集合中取一个最小的表达式作为当前变量的值编号，如果一个表达式是运算符表达式，取最小两个表达式的运算结果作为值编号。