【方差分析原理简介】-编程知识

文章目录

方差分析（Analysis of Variance，简称ANOVA）
- 1 方差分析流程
- 2 借助sklean进行基于方差分析的特征筛选
- 3 总结

方差分析（Analysis of Variance，简称ANOVA）

卡方检验更多的会考虑在衡量两个离散变量是否独立时使用，如果是连续变量和离散变量之间的独立性，更常见的做法是进行方差分析。

1 方差分析流程

Step 1.提出假设
Step 2.采集数据
这里我们还是以鸢尾花数据集为例

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
import numpy as np# 加载示例数据集
iris = load_iris()
X, y = iris.data, iris.target
X = pd.DataFrame(X,columns=iris.feature_names)

在这里插入图片描述
我们就petal length (cm)字段和标签进行分析

#根据标签快速分组
cat_0 = X["petal length (cm)"][y==0]
cat_1 = X["petal length (cm)"][y==1]
cat_2 = X["petal length (cm)"][y==2]

Step 3.设计统计量
最关键的环节，肯定就是如何构造统计量来判断两类样本均值差异程度了。这里我们需要借助此前我们曾介绍的一组概念，这组概念曾在线性回归以及K-Means快速聚类中提及，是一组专门用来衡量整体误差、组内误差和组间误差的概念。这里我们再通过严谨的数学公式描述一遍。假设目前有n条数据被分成k组（即标签有k个类别），其中第j个类别中包含 $n_j$ 条样本，并且 $x_{i,j}$ 表示第j个类别的第i条样本，则有样本整体偏差计算公式如下：
$\sum^k_{j=1}\sum^{n_j}_{i=1}(x_{ij}-\bar x)^2$
及样本与均值的差值平方和，此处 $\bar x = \frac{\sum^k_{j=1}\sum^{n_j}_{i=1}x_{ij}}{n}$
而如果我们更进一步，计算每个组内的样本与均值的差值的平方和，则可以算得如下结果：
$SSE_j = \sum^{n_j}_{i=1}(x_{ij}-\bar {x_j})^2$
即第j组的组内偏差平方和，其中 $\bar {x_j} = \frac{\sum_{i=1}^{n_j}x_{ij}}{n_j}$ ，为第j组数据的组内均值。而k个分组的组内偏差总和为：
$\sum_{j=1}^k SSE_j = \sum_{j=1}^k\sum^{n_j}_{i=1}(x_{ij}-\bar {x_j})^2$
SSE即为组内偏差平方和。此时（在欧式空间情况下）则可以通过数学公式推导得出，SST和SSE之间的差值如下：
$SSB=SST-SSE=\sum_{j=1}^k n_j (\bar{x_j}-\bar x)^2$
即每个组的均值和总体均值的差值的平方加权求和的结果，其中权重就是每个组的样本数量。SSB也被称为组间偏差平方和。
我们就找到了如何衡量不同组均值差异的基础理论工具，接下来需要进一步的构造统计检验量，来更具体的量化的表示这种均值差异程度。此处构造的统计检验量就是F，F计算公式如下：
$F=\frac{MSB}{MSE}=\frac{SSB/df_B}{SSE/df_E}=\frac{SSB/(k-1)}{SSE/(n-k)}$
此处 $df_b$ 就是统计量SSB的自由度，类似于卡方检验过程中(行数-1*列数-1)用于修正卡方值， $df_b$ 也是一个用于修正SSB计算量的值——为了防止分组的数量影响了SSB的计算结果；类似的 $df_E$ 就是SSE的自由度，用于修正样本数量对SSE计算结果的影响。目前来说我们并不用深究自由度的学术含义，只需要知道统计检验量会利用自由度对统计量进行数值上的修正，并且这些修正的值会在最一开始就确定，例如k（分成几类）、n（数据总量）等，并不会受到实际数据取值大小的影响。
Step 4-5.事件发生概率计算与统计推断

k = len(np.unique(y))
n = len(y)
k, n

在这里插入图片描述

cat_0_mean = cat_0.mean()
cat_1_mean = cat_1.mean()
cat_2_mean = cat_2.mean()SSE0 = np.power(cat_0 - cat_0_mean, 2).sum()
SSE1 = np.power(cat_1 - cat_1_mean, 2).sum()
SSE2 = np.power(cat_2 - cat_2_mean, 2).sum()SSE = SSE0 + SSE1+ SSE2
SSE

在这里插入图片描述

n0 = len(cat_0)
n1 = len(cat_1)
n2 = len(cat_2)cat_mean = X["petal length (cm)"].mean()SSB = n0 * np.power(cat_0_mean-cat_mean, 2) + n1 * np.power(cat_1_mean-cat_mean, 2) + n2 * np.power(cat_2_mean-cat_mean, 2)SSB

在这里插入图片描述

SST = np.power( X["petal length (cm)"] - cat_mean, 2).sum()
SST

在这里插入图片描述

#可以很简单检验SSE和SSB之和是否会等于SST
SSB + SSE

在这里插入图片描述

MSB = SSB/(k-1)
MSE = SSE/(n-k)F_score = MSB/MSE
F_score

在这里插入图片描述

import scipy
scipy.special.fdtrc(k-1, n-k, F_score)#scipy.special.fdtrc进行p值计算

在这里插入图片描述
概率几乎为零，也就是说零假设成立的概率几乎为零，我们可以推翻零假设，即petal length (cm)和标签存在显著差异。进一步应用到特征筛选环节，得到的结论就是petal length (cm)和标签存在显著的关联关系。
我们也可以借助scipy中的stats.f_oneway函数直接进行方差分析计算，此处仅需带入两类不同的样本即可:

scipy.stats.f_oneway(cat_0, cat_1,cat_2)

在这里插入图片描述
能够发现计算结果和手动计算结果一致。

尽管我们在方差分析中用到了F检验，但方差分析不同于F检验。F检验泛指一切借助F值进行检验的过程，而方差分析只是其中一种。换而言之，只要假设检验中的检验统计量满足F分布，则该过程就用到了F检验。另外需要拓展了解的一点是，除了方差分析以外，还有一种检验也能判断两个样本的均值是否一致，也就是t检验。所不同的是，方差分析能够同时检验多个样本，也就是如果是三分类标签、则对应三个不同的样本，卡方检验能够同时判断三个样本是否取自同一总体，进而判断该特征是否可用（从特征筛选的角度来看）。而t检验只能两两比较，很明显应如果是用于特征筛选环节，t检验并不够高效。而t检验、卡方检验和方差分析，被称作统计学三大检验。

2 借助sklean进行基于方差分析的特征筛选

我们来看在sklearn如何借助方差分析来完成特征筛选。这里需要借助f_classif评估函数来实现方差分析的过程：

from sklearn.feature_selection import f_classif
f_classif(X["petal length (cm)"].values.reshape(-1, 1),y.ravel())

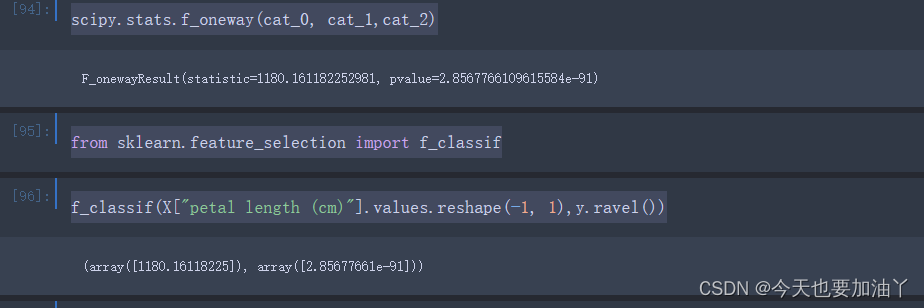
在这里插入图片描述
sklearn中的f_classif也就是调用f_oneway函数进行的计算，因此最终输出结果和此前实验结果完全一致。同时f_classif本身也是评分函数，输出的F值就是评分。很明显F值越大、p值越小、我们就越有理由相信两列存在关联关系，反之F值越小则说明两列没有关系，可以考虑剔除。

接下来我们借助SelectKBest来进行基于方差分析评分的特征筛选，注意仅针对两个连续变量进行方差分析检验特征筛选(其中定义的SelectName函数在卡方检验中有）
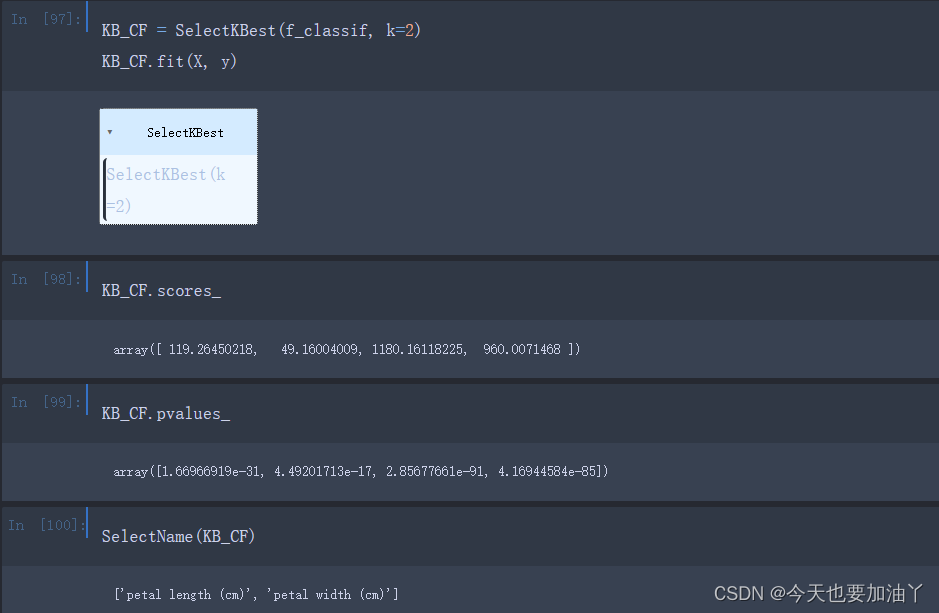
在这里插入图片描述

3 总结

如果是针对分类问题，f_classif与chi2两个评分函数搭配使用，就能够完成一次完整的特征筛选，其中chi2用于筛选离散特征、f_classif用于筛选连续特征。而如果是回归问题，sklearn提供了一种基于F检验的线性相关性检验方法f_regression，该检验方法并不常见。需要注意，该方法只能用于回归问题中，并且只能筛选出与标签呈现线性相关关系的连续变量。