C++力扣题目112，113--路径总和，路径总和II-编程知识

112路径总和给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

思路

相信很多同学都会疑惑，递归函数什么时候要有返回值，什么时候没有返回值，特别是有的时候递归函数返回类型为bool类型。

那么接下来我通过详细讲解如下两道题，来回答这个问题：

112.路径总和(opens new window)
113.路径总和ii(opens new window)

这道题我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。

#递归

可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

确定递归函数的参数和返回类型

参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。（这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

如图所示：

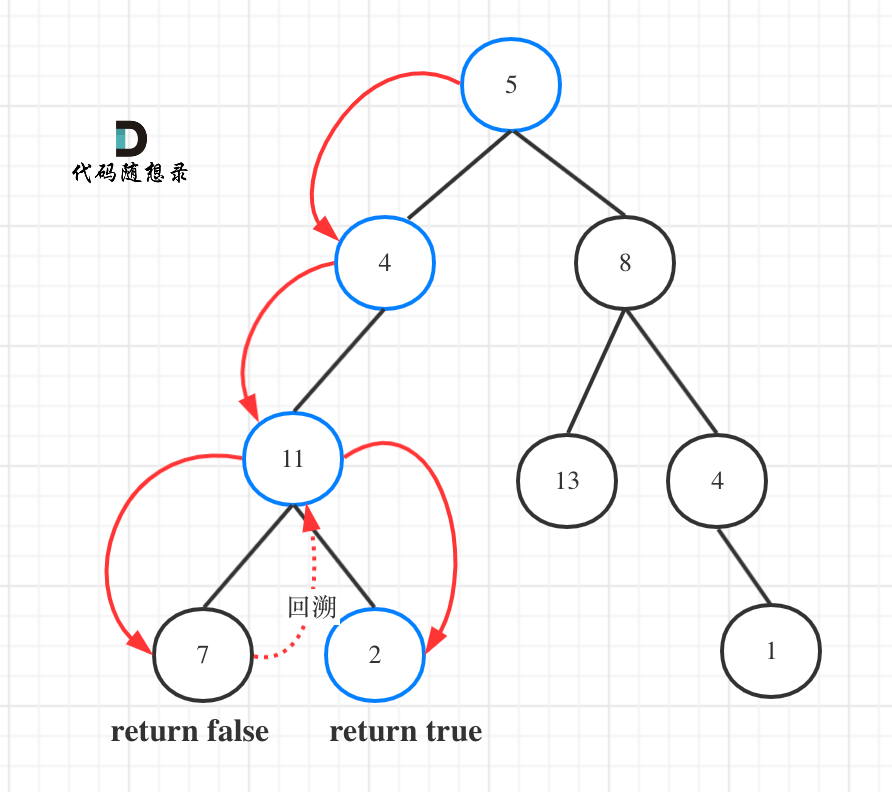
112.路径总和

图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

所以代码如下：

bool traversal(treenode* cur, int count)   // 注意函数的返回类型

确定终止条件

首先计数器如何统计这一条路径的和呢？

不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

如果遍历到了叶子节点，count不为0，就是没找到。

递归终止条件代码如下：

if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点而没有找到合适的边，直接返回

确定单层递归的逻辑

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。

递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

代码如下：

if (cur->left) { // 左 （空节点不遍历）// 遇到叶子节点返回true，则直接返回trueif (traversal(cur->left, count - cur->left->val)) return true; // 注意这里有回溯的逻辑
}
if (cur->right) { // 右 （空节点不遍历）// 遇到叶子节点返回true，则直接返回trueif (traversal(cur->right, count - cur->right->val)) return true; // 注意这里有回溯的逻辑
}
return false;

以上代码中是包含着回溯的，没有回溯，如何后撤重新找另一条路径呢。

回溯隐藏在traversal(cur->left, count - cur->left->val)这里，因为把count - cur->left->val 直接作为参数传进去，函数结束，count的数值没有改变。

为了把回溯的过程体现出来，可以改为如下代码：

if (cur->left) { // 左count -= cur->left->val; // 递归，处理节点;if (traversal(cur->left, count)) return true;count += cur->left->val; // 回溯，撤销处理结果
}
if (cur->right) { // 右count -= cur->right->val;if (traversal(cur->right, count)) return true;count += cur->right->val;
}
return false;

整体代码如下：

class Solution {
private:bool traversal(TreeNode* cur, int count) {if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回if (cur->left) { // 左count -= cur->left->val; // 递归，处理节点;if (traversal(cur->left, count)) return true;count += cur->left->val; // 回溯，撤销处理结果}if (cur->right) { // 右count -= cur->right->val; // 递归，处理节点;if (traversal(cur->right, count)) return true;count += cur->right->val; // 回溯，撤销处理结果}return false;}public:bool hasPathSum(TreeNode* root, int sum) {if (root == NULL) return false;return traversal(root, sum - root->val);}
};

以上代码精简之后如下：

class Solution {
public:bool hasPathSum(TreeNode* root, int sum) {if (!root) return false;if (!root->left && !root->right && sum == root->val) {return true;}return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);}
};

是不是发现精简之后的代码，已经完全看不出分析的过程了，所以我们要把题目分析清楚之后，再追求代码精简。 这一点我已经强调很多次了！

#迭代

如果使用栈模拟递归的话，那么如果做回溯呢？

此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。

c++就我们用pair结构来存放这个栈里的元素。

定义为：pair<TreeNode*, int> pair<节点指针，路径数值>

这个为栈里的一个元素。

如下代码是使用栈模拟的前序遍历，如下：（详细注释）

class solution {public:bool haspathsum(TreeNode* root, int sum) {if (root == null) return false;// 此时栈里要放的是pair<节点指针，路径数值>stack<pair<TreeNode*, int>> st;st.push(pair<TreeNode*, int>(root, root->val));while (!st.empty()) {pair<TreeNode*, int> node = st.top();st.pop();// 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回trueif (!node.first->left && !node.first->right && sum == node.second) return true;// 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来if (node.first->right) {st.push(pair<TreeNode*, int>(node.first->right, node.second + node.first->right->val));}// 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来if (node.first->left) {st.push(pair<TreeNode*, int>(node.first->left, node.second + node.first->left->val));}}return false;}
};

如果大家完全理解了本题的递归方法之后，就可以顺便把leetcode上113. 路径总和ii做了。

#相关题目推荐

#113. 路径总和ii

力扣题目链接(opens new window)

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

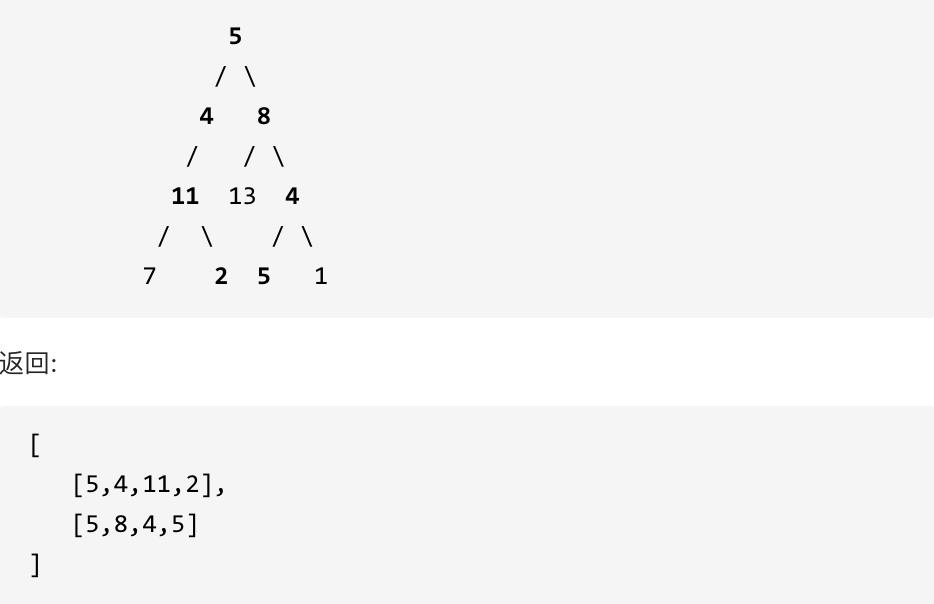
113.路径总和ii1.png

#思路

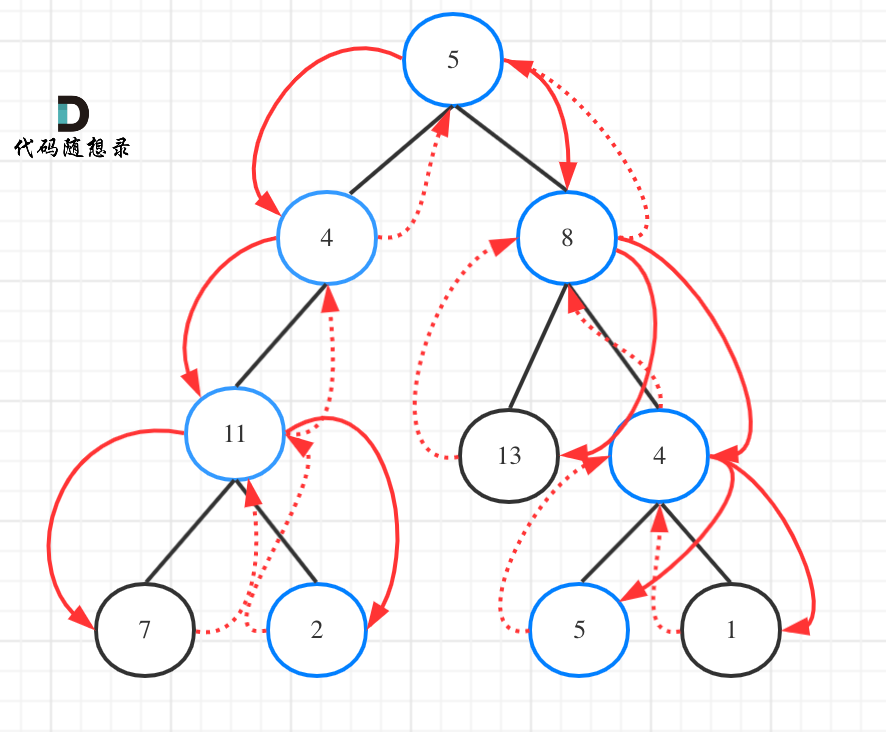
113.路径总和ii要遍历整个树，找到所有路径，所以递归函数不要返回值！

如图：

113.路径总和ii

为了尽可能的把细节体现出来，我写出如下代码（这份代码并不简洁，但是逻辑非常清晰）

class solution {
private:vector<vector<int>> result;vector<int> path;// 递归函数不需要返回值，因为我们要遍历整个树void traversal(TreeNode* cur, int count) {if (!cur->left && !cur->right && count == 0) { // 遇到了叶子节点且找到了和为sum的路径result.push_back(path);return;}if (!cur->left && !cur->right) return ; // 遇到叶子节点而没有找到合适的边，直接返回if (cur->left) { // 左 （空节点不遍历）path.push_back(cur->left->val);count -= cur->left->val;traversal(cur->left, count);    // 递归count += cur->left->val;        // 回溯path.pop_back();                // 回溯}if (cur->right) { // 右 （空节点不遍历）path.push_back(cur->right->val);count -= cur->right->val;traversal(cur->right, count);   // 递归count += cur->right->val;       // 回溯path.pop_back();                // 回溯}return ;}public:vector<vector<int>> pathSum(TreeNode* root, int sum) {result.clear();path.clear();if (root == NULL) return result;path.push_back(root->val); // 把根节点放进路径traversal(root, sum - root->val);return result;}
};

至于113. 路径总和ii 的迭代法我并没有写，用迭代方式记录所有路径比较麻烦，也没有必要，如果大家感兴趣的话，可以再深入研究研究。