互信息法（上）

尽管f_regression巧妙的构建了一个F统计量，并借此成功的借助假设检验来判断变量之间是否存在线性相关关系，但f_regression仍然存在较大局限，首当其冲当然是f_regression只能挖掘线性相关关系，也就是两个变量的同步变化关系，但除了线性关联关系外，变量之间存在其他类别的“关联关系”也是有助于模型建模，而其他类型的关系，无法被f_regression识别；其二就是由于离散变量（尤其是名义型变量）的数值大小是没有意义的，因此判断离散变量和其他变量的“线性关系”意义不大，因此f_regression只能作用于两个连续变量之间。综上所述，f_regression唯一适用的场景就是用于线性回归的连续变量特征筛选的过程中。而对于机器学习，针对于回归类问题，仅仅依靠f_regression进行连续型变量的特征筛选肯定是远远不够的。接下来我们就进一步介绍可以挖掘除了线性相关关系外的特征筛选方法：互信息法。

互信息是什么

从信息增益角度理解互信息

理解信息增益的求算过程，我们先了解一下信息熵。信息熵的计算公式：
$$H(X)=-\sum _{i=1}^{n}p(x_i)log(p(x_i))$$
其中，$p(x_i)$表示多分类问题中第$i$个类别出现的概率，$n$表示类别总数，通常来说信息熵的计算都取底数为2，并且规定$log0=0$。
假设有二分类数据集如下：

index	labels
1	0
2	1
3	1
4	1

该数据集的信息增益为：
$$\begin{array}{rl}H(X)& =-(p(x_1)log(p(x_1))+p(x_2)log(p(x_2)))\\ & =-(\frac{1}{4})log(\frac{1}{4})-(\frac{3}{4})log(\frac{3}{4})\end{array}$$

-1/4 * np.log2(1/4) - 3/4 * np.log2(3/4)

#也可以借助scipy中的stats.entropy函数来完成信息熵的计算
scipy.stats.entropy([1/4, 3/4], base=2)#base等于2，表示log以2为底

如现有简单数组如下，在按照特征对标签进行分组后，各数据集的信息熵计算结果如下：

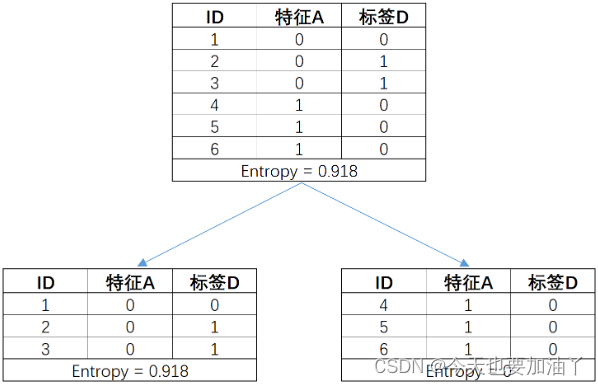
# 原数据集信息熵
ent_A = 0.918# 子数据集整体信息熵，各个子数据集信息熵加权求和
ent_B = 1/2 * 0.918 + 1/2 * 0#计算信息增益
gain = ent_A - ent_B
gain

而这也是ID 3决策树的基本建树流程，即找到最能够降低子数据集标签不纯度的特征对数据集进行划分，而这里的信息增益，其实也就是这个降低不纯度的量化的指标。

互信息的解释: 参考视频

所以从本质上来讲，互信息就是信息增益

所以为什么树模型以及以树模型为弱分类器的集成算法可以不进行特征筛选？
不难发现，原因是树模型的生长过程其实是会自动选取信息增益最大的列进行数据集划分（即树的生长）特征筛选的（CART树也有类似过程，只不过更换了信息熵为基尼系数）

互信息这一指标的实际作用，确实能够挑选出能有效帮助模型建模的特征。而互信息法的本质，我们也可以将其理解为一个剥离决策树模型训练、单纯只对每个特征进行互信息计算、然后根据互信息进行挑选特征的过程。

我们也可以借助sklearn中的相关函数来更加自动化的执行互信息的计算，对于上述分类变量的互信息计算过程，可以借助sklearn中评估函数的mutual_info_score来完成计算：

from sklearn.metrics import mutual_info_score
A = np.array([0, 0, 0, 1, 1, 1])
D = np.array([0, 1, 1, 0, 0, 0])
mutual_info_score(A, D)
mutual_info_score(D, A)

这里需要说明的两点是：

1. mutual_info_score(A,D)和mutual_info_score(D,A)的计算结果是一样的，这是因为互信息具有对称性，用A解释D，也可以用D解释A；
2. sklearn中互信息的计算是以e为底的。

从变量分布一致角度理解互信息

假设有下面数据表：

特征A	标签D
0	0
0	1
0	1
1	0
1	0
1	0

p_A0 = 1/2
p_A1 = 1/2
p_D0 = 2/3
p_D1 = 1/3p_A0D0 = 1/6
p_A0D1 = 1/3
p_A1D0 = 1/2
p_A1D1 = 0KL_AD = p_A0D0 * np.log(p_A0D0/(p_A0*p_D0)) + p_A0D1 * np.log(p_A0D1/(p_A0*p_D1)) + p_A1D0 * np.log(p_A1D0/(p_A1*p_D0))
KL_AD

A = np.array([0, 0, 0, 1, 1, 1])
D = np.array([0, 1, 1, 0, 0, 0])
mutual_info_score(D, A)

和信息增益最终计算结果完全一致。

卡方检验与离散变量的互信息法

首先也是最明显的一点，就是卡方检验能够给出明确的p值用于评估是否是小概率事件，而互信息法只能给出信息增益的计算结果，很多时候由于信息增益的计算结果是在0到最小信息熵之间取值，因此信息增益的数值在判断特征是否有效时并不如p值那么直观。

其次需要注意的是，卡方检验的p值源于假设检验统计量服从卡方分布，这种有假设分布的方法也被称为参数方法，而互信息法并不涉及任何假定的参数分布，因此是一种非参数方法。不难发现，参数方法是借助样本估计总体，然后根据总体进行推断的过程，而非参数方法则无需总体信息即可计算。尽管从方法理解层面来看非参数方法会更加简单，但这种“简单”所带来的代价，就是非参数方法无法对小样本进行合理的预估。
 
 卡方检验是会收到样本数量影响的，而此时卡方检验不敢下结论的原因或许并不是因为现在的A和D表现出来的关联性不够强，而是目前样本数量太少了（只有六条样本）。因此这里如果我们不改变A和D的数据分布，而仅仅将样本数量扩增至10倍，则卡方检验结果如下：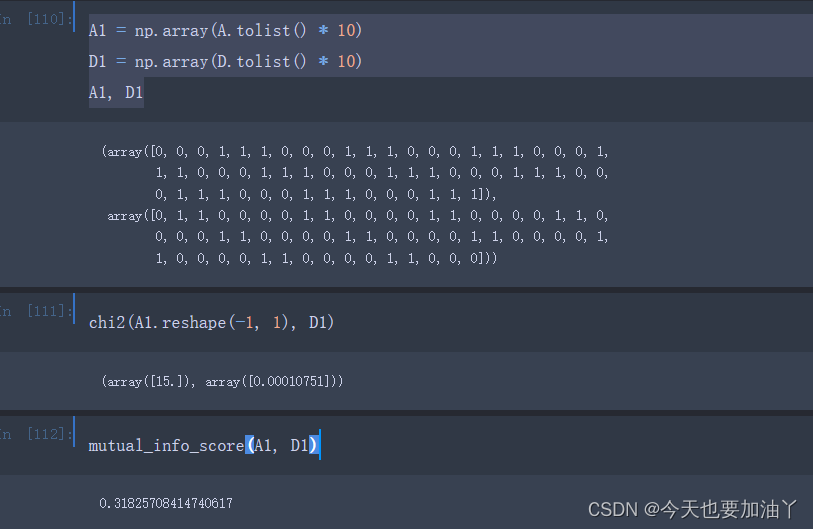
能够发现，此时卡方检验认为当前数据情况下A1和D1相互独立就是一个非常小概率的事件了，即判断A1和D1存在显著的关联关系。但此时互信息的计算结果仍然不变。

而这将如何影响我们对这两种方法的选用呢？一般来说，对于小样本而言，卡方检验的结果可信度会高于互信息法，因此优先考虑卡方检验，而对于大样本而言，卡方检验和互信息法二者的结果其实并不会有特别大的差异，卡方检验的p值越小、互信息的值就会越大、二者关联度就越高。对于大样本数据，若最终采用模型融合策略进行建模，则最好采用不同的特征筛选方法训练不同模型，以期能达到更好的融合效果。最后，需要强调的是，如果分类变量样本偏态非常严重，也会影响互信息的结果，但不会影响卡方检验结果。