题目
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = “bbbab”
输出:4
解释:一个可能的最长回文子序列为 “bbbb” 。
示例 2:
输入:s = “cbbd”
输出:2
解释:一个可能的最长回文子序列为 “bb” 。
提示:
1 <= s.length <= 1000
s 仅由小写英文字母组成
解题思路
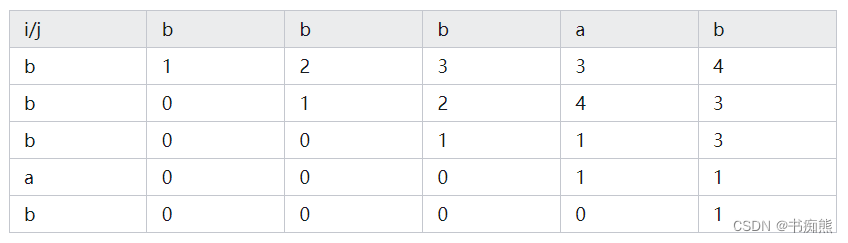
使用动态规划,定义dp[i][j]为字符串区间[i,j]的最长回文序列的长度。如果i=j,则dp[i][j]为1,可根据这个初始化dp[i][j]数组。根据s[i]和s[j]是否相等,可以得到,如果相等,则dp[i][j]可由dp[i+1][j-1]推导得到;如果不相等,则dp[i][j]为dp[i][j+1]和dp[i+1][j]的最大值得到。最后返回[i,j]区间为s长度的结果。
代码实现
class Solution {
public:int longestPalindromeSubseq(string s) {if (s.empty()) return 1;vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i=s.size()-1;i>=0;i--) {for (int j=i+1;j<s.size();j++) {if (s[i]==s[j]) {dp[i][j] = dp[i+1][j-1] + 2;} else {dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][s.size()-1];}
};