前言
二分图,又称二部图,英文名叫 Bipartite graph。
通俗一点就是一个无向图如果能划成两个非空点集,且两部分内部没有边,则这是一张二分图。
如果从颜色的角度来说,就是把节点染成黑色/白色,并且使得没有相邻的节点颜色相同。
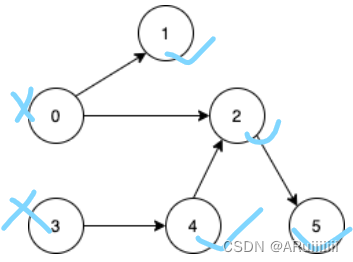
一张二分图:

二分图判定
奇环:长度为奇数的环
一张无向图 G G G为二分图的充要条件是:图中不存在奇环
证明:
必要性显然,因为奇环显然不是二分图。
充分性:只需证明没有奇环的图就是二分图
考虑无向图 G G G没有奇环且连通,若不连通可以对每个连通块单独考虑。
从节点 x x x开始染色,把 x x x染成白色,找到节点 x x x到图中所有点的所有路径,对于一条从 x x x到 y y y的路径 ( u 0 = x , u 1 , u 2 , . . . , u k = y ) (u_0=x,u_1,u_2,...,u_k=y) (u0=x,u1,u2,...,uk=y),我们把 u i ∈ 奇数 u_{i\in 奇数} ui∈奇数染黑,把 u i ∈ 偶数 u_{i\in 偶数} ui∈偶数染白。
- 如果这个操作中一个点只被染成了一种颜色,那我们就构造出了一张二分图的划分
- 如果存在一个点被染成了两种颜色,那么说明它在某两条路径到 x x x的路径中分别位于奇数位置和偶数位置,这时候我们把这两条路径拼起来,就得到了一个奇环,矛盾。
QED.
但是二分图判定的代码并不是找奇环的,而是dfs/bfs染色,因为图中环的个数是指数级的,找奇环是很亏的。
dfs/bfs判奇环复杂度为 O ( n + m ) O(n+m) O(n+m)
二分图最大匹配:匈牙利算法
由于作者实力不济,本文没有匈牙利算法的证明。
匈牙利算法大概的过程是:
- 对每个左部点 i i i执行一遍
dfs(i),保证每一次期间,执行一个右部点只会被访问一次 dfs(u)的过程是:- 遍历左部点 u u u的未被访问的右部点 v v v
- 标记 v v v
- 检查 v v v是否有
match,如果没有抢,如果有,就dfs(match[v])看看能不能抢
时间复杂度 O ( l ⋅ m + r ) O(l\cdot m+r) O(l⋅m+r),其中 l l l是左部点数量, m m m是边数, r r r是右部点数量。
实现
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int N=500;
vector<int> a[N+5];
int match[N+5];
bool vis[N+5];
bool dfs(int u) {for(auto&v:a[u])if(!vis[v]) {vis[v]=1;if(!match[v]||dfs(match[v]))return (match[v]=u);}return 0;
}
int main() {int l,r,m;cin>>l>>r>>m;for(int i=1,u,v;i<=m;i++){cin>>u>>v;a[u].push_back(v);}int ans=0;for(int i=1;i<=l;i++,memset(vis,0,sizeof vis))ans+=dfs(i);cout<<ans;}
后记
于是皆大欢喜。