一元线性回归模型（公式推导+举例应用）-编程知识

一元线性回归模型（公式推导+举例应用）

文章目录

- - 引言
  - 模型表达式
  - 均方误差和优化目标
  - 最小二乘法
  - 利用协方差和方差求解 $k$ 和 $b$
  - 结论
  - 实验分析

引言

一元线性回归是回归分析中简单而重要的一种模型，旨在找到一条直线，以最佳方式拟合输入变量与输出变量之间的关系。在这篇文章中，我们将深入探讨一元线性回归的原理及其应用。

模型表达式

一元线性回归模型的表达式为： $f(x_i)=kx_i+b$
其中， $x_i$ 为输入变量， $f(x_i)$ 为模型的输出， $k$ 为斜率， $b$ 为截距，我们的目标是通过学习 $k$ 和 $b$ 使得 $f(x_i)$ 尽可能的接近真实观测值 $y_i$ 。

均方误差和优化目标

为了衡量模型的性能，我们引入均方误差 $J (k, b) :$
$J(k,b)=\sum_{i=1}^m(f(x_i)-y_i)^2$
其中 $m$ 为样本数量。我们的优化目标是最小化均方误差，即：

$E(k^\star,b^\star)=arg_{(k,b)}min\sum_{i=1}^m(y_i-kx_i-b)^2$

最小二乘法

通过最小二乘法，我们对均方误差函数分别对 $k$ 和 $b$ 求偏导数，令其等于零，得到优化的解：
$\frac{\partial}{\partial k} E(k, b)=-2\sum_{i=1}^n x_i\left(y_i-\left(k x_i+b\right)\right)=0$
$\frac{\partial}{\partial b} E(k, b)=-2\sum_{i=1}^n\left(y_i-\left(k x_i+b\right)\right)=0$
整理并得到：
$k=\frac{\sum_{i=1}^my_i(x_i- \bar x)}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2}$
$b=\frac{1}{m}\sum_{i=1}^m(y_i-kx_i)$
其中， $\bar x$ 为输入变量 $x$ 的均值。最终得到模型表达式：
$f(x_i)=k^Tx_i+b$
使得 $f(x_i)$ 尽可能地接近 $y_i$ 。

利用协方差和方差求解 $k$ 和 $b$

另一种求解斜率 $k$ 和截距 $b$ 的方法是通过协方差和方差的关系。
因为 $Y = k X + b$ ，所以 $E Y = k EX + b$
又因为 $XY=kX^2+bX$ ，所以 $EXY=kEX^2+bEX$
联立两个式子可得：
$k=\frac{EXY-EXEY}{EX^2-(EX)^2}=\frac{COV(X,Y)}{DX}$
$b = E Y - k EX$
我们同样可以得到一元线性回归模型 $f(x_i)=k^Tx_i+b$

结论

通过最小二乘法和协方差方差的推导，我们得到了一元线性回归的两种求解方法。这些方法为我们建立模型和预测提供了有力的工具，同时也帮助我们理解了回归分析的基本原理。在实际应用中，我们可以根据具体情况选择合适的方法来进行建模和分析。

实验分析

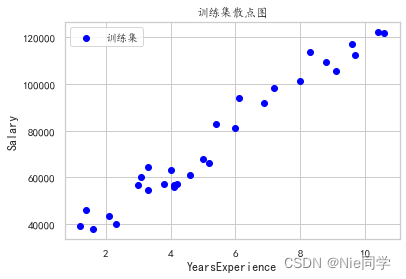
以下是工人工作年限与对应薪水的数据集。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="deep")
# 读入数据集
data = pd.read_csv('data/Salary_dataset.csv')
# 绘制散点图
plt.rcParams['font.family'] = 'KaiTi'
plt.scatter(data['YearsExperience'], data['Salary'], c='blue', label='训练集')# 添加标签和标题
plt.xlabel('x')
plt.ylabel('y')
plt.title('训练集散点图')# 添加图例
plt.legend()# 显示图形
plt.show()

在这里插入图片描述

# 更新k,b(协方差)
def update_k_b(data, k, b):# 计算协方差和方差cov_xy = np.sum((data['YearsExperience'] - data['YearsExperience'].mean()) * (data['Salary'] - data['Salary'].mean()))var_x = np.sum((data['YearsExperience'] - data['YearsExperience'].mean())**2)# 计算k和bk = cov_xy / var_xb = data['Salary'].mean() - k * data['YearsExperience'].mean()return k, b
# 更新k,b（最小二乘法）
def update_k_b_2(data, k, b):w = np.sum(data['Salary'] * (data['YearsExperience'] - data['YearsExperience'].mean())) / (np.sum(data['Salary'] ** 2) - np.sum(data['Salary']) ** 2 / len(data))b = data['Salary'].mean() - k * data['YearsExperience'].mean()return k, b

计算 $k$ 和 $b$

k = b = 0
k, b = update_k_b(data, k, b)

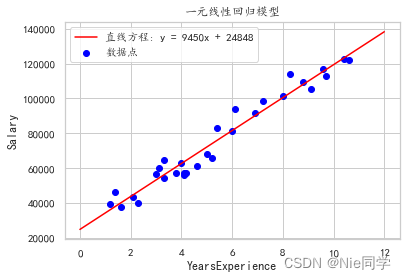
得到 $k = 9449.962321455076$ ， $b = 24848.2039665232$ 。
绘制最终的拟合直线：

# 绘制散点图
plt.rcParams['font.family'] = 'KaiTi'
plt.scatter(data['YearsExperience'], data['Salary'], c = 'blue', label = '数据点')# 生成一些x值
x_line = np.linspace(0, 12, 100)# 根据直线方程计算对应的y值
y_line = k * x_line + b# 绘制直线图
plt.plot(x_line, y_line, label = f'直线方程: y = {k:.0f}x + {b:.0f}', c = 'red')# 添加标签和标题
plt.xlabel('YearsExperience')
plt.ylabel('Salary')
plt.title('一元线性回归模型')# 添加图例
plt.legend()# 显示图形
plt.show()