42. 接雨水
题目链接:42. 接雨水
思路:本题十分经典,使用单调栈需要理解的几个问题:
-
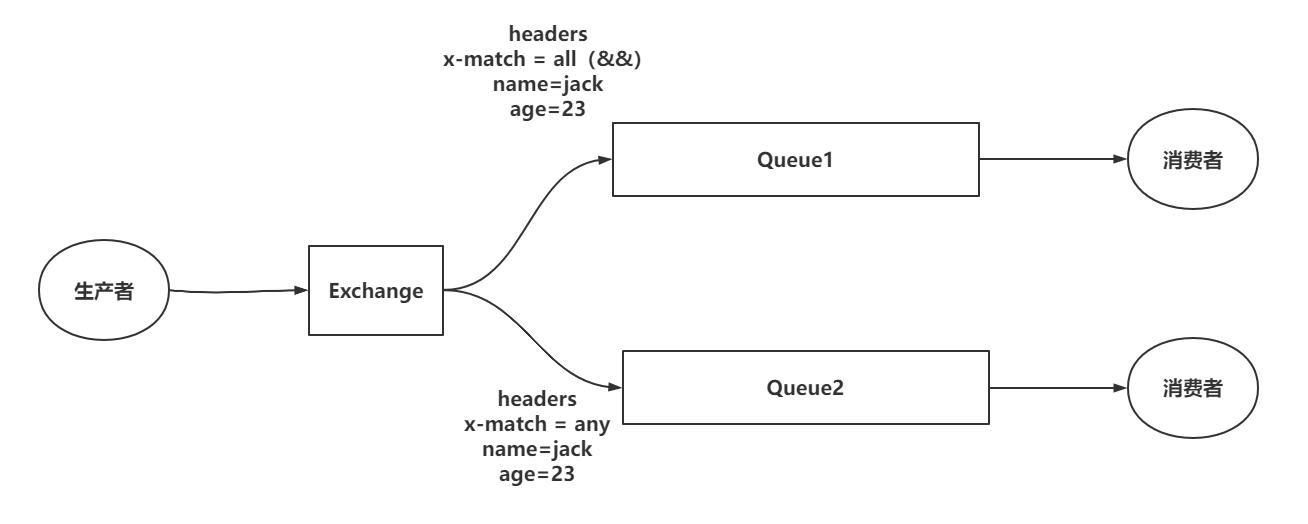
首先单调栈是按照行方向来计算雨水,如图:

-
使用单调栈内元素的顺序
从大到小还是从小到大呢?
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
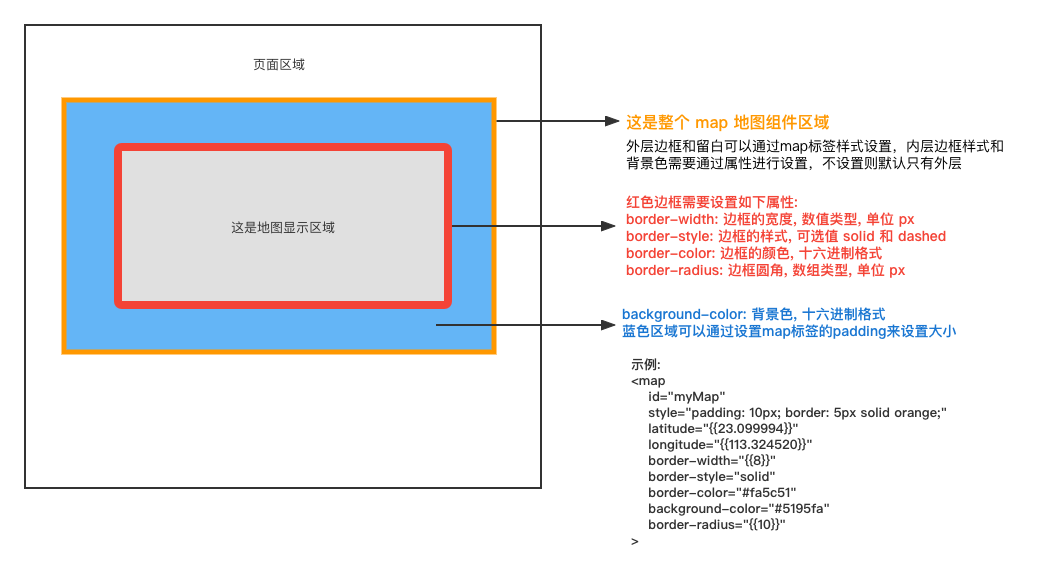
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
如图:
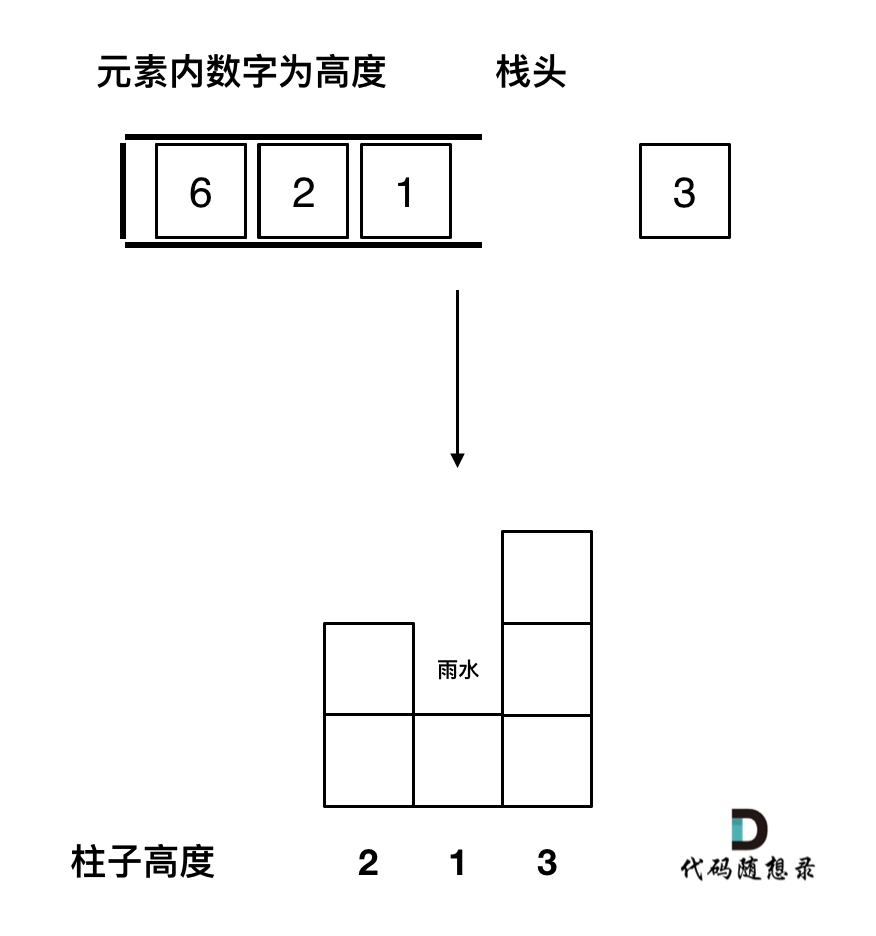
关于单调栈的顺序:739. 每日温度中求一个元素右边第一个更大元素,单调栈就是递增的,84.柱状图中最大的矩形求一个元素右边第一个更小元素,单调栈就是递减的。
-
遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中,需要使用最右边的柱子来计算宽度。
-
栈里要保存什么数值
栈里就存放下标就行,想要知道对应的高度,通过height[stack.peek()] 就知道弹出的下标对应的高度了。
class Solution {public int trap(int[] height) {// 找每个柱子左右两边第一个大于该柱子高度的柱子int res = 0;Deque<Integer> stack = new LinkedList<>();stack.push(0);for (int i = 1; i < height.length; i++) {if (height[i] < height[stack.peek()]) {// 情况一stack.push(i);} else if (height[i] == height[stack.peek()]) {// 情况二stack.pop();stack.push(i);} else {// 情况三while (!stack.isEmpty() && height[i] > height[stack.peek()]) {int mid = stack.pop(); // 凹槽的底部,也就是中间位置if (!stack.isEmpty()) {int left = stack.peek();int h = Math.min(height[left], height[i]) - height[mid];int w = i - left - 1; // 注意减一,只求中间宽度res += h * w;}}stack.push(i);}}return res;}
}
双指针解法如下:
class Solution {public int trap(int[] height) {int n = height.length;int res = 0;// 数组充当备忘录int[] l_max = new int[n];int[] r_max = new int[n];// 初始化 base casel_max[0] = height[0];r_max[n - 1] = height[n - 1];// 从左向右计算 l_maxfor (int i = 1; i < n; i++)l_max[i] = Math.max(height[i], l_max[i - 1]);// 从右向左计算 r_maxfor (int i = n - 2; i >= 0; i--)r_max[i] = Math.max(height[i], r_max[i + 1]);// 计算答案for (int i = 1; i < n - 1; i++)res += Math.min(l_max[i], r_max[i]) - height[i];return res;}
}
为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。把每一个位置的左边最高高度记录在一个数组上(l_max),右边最高高度记录在一个数组上(r_max),这样就避免了重复计算。
84. 柱状图中最大的矩形
题目链接:84. 柱状图中最大的矩形
思路:本题十分适合与接雨水对照来看,接雨水是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子高度的柱子。
本题与接雨水最主要的区别在于单调栈中存放元素的顺序不同。其他步骤与接雨水的分析过程相同。
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
所以本题单调栈的顺序正好与接雨水反过来。(栈顶和栈顶的下一个元素以及要入栈的三个元素组成了要求最大面积的高度和宽度)
class Solution {public int largestRectangleArea(int[] heights) {// 找每个柱子左右两边第一个小于该柱子高度的柱子int res = 0;Deque<Integer> stack = new LinkedList<>();// 数组前后各加一个0int[] newHeights = new int[heights.length + 2];newHeights[0] = 0;newHeights[newHeights.length - 1] = 0;for (int i = 0; i < heights.length; i++) {newHeights[i + 1] = heights[i];}stack.push(0);// 开始遍历for (int i = 1; i < newHeights.length; i++) {if (newHeights[i] > newHeights[stack.peek()]) {// 情况一stack.push(i);} else if (newHeights[i] == newHeights[stack.peek()]) {// 情况二stack.pop();stack.push(i);} else {// 情况三while (!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]) {int mid = stack.pop();if (!stack.isEmpty()) {int left = stack.peek();int h = newHeights[mid];int w = i - left - 1;res = Math.max(res, h * w);}}stack.push(i);}}return res;}
}
在 height数组上后,都加了一个元素0, 为什么这么做呢?
首先来说末尾为什么要加元素0?
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。
开头为什么要加元素0?
如果数组本身降序,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时得到 mid(8),right(6),但是得不到 left。因为将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑。之后又将6 加入栈(此时8已经弹出了),然后就是 4 与栈口元素 8 进行比较,周而复始,那么计算的最后结果result就是0。