实验一、数论基础(上)
一、实验目的
1、通过本次实验,熟悉相关的编程环境,为后续的实验做好铺垫;
2、回顾数论学科中的重要基本算法,并加深对其的理解,为本学期密码学理论及实验课程打下良好的基础。
二、实验原理
数论主要研究的是整数的运算及性质,许多常用的加密算法都用到了数论知识。
三、实验环境
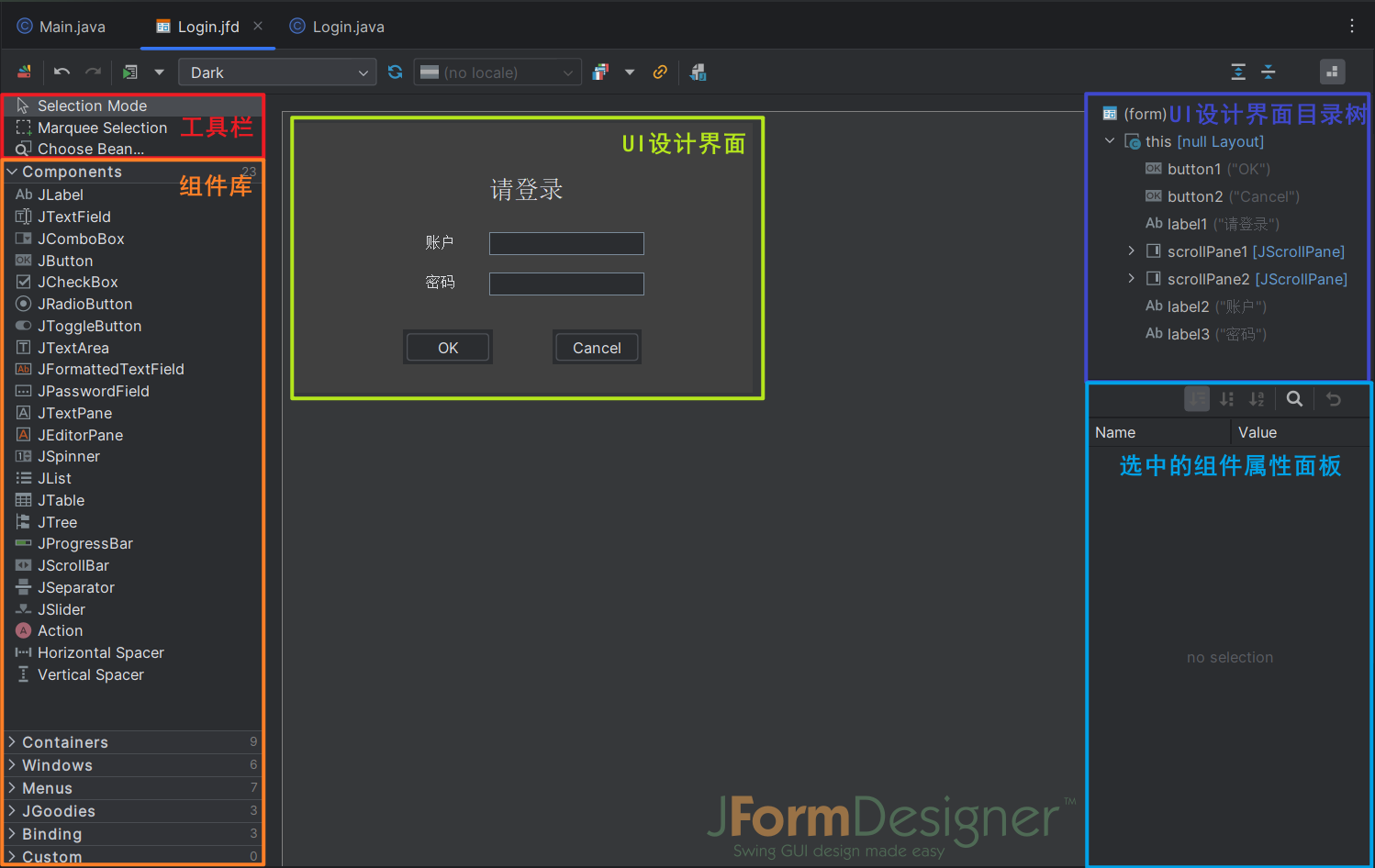
本次实验的实验环境为Dev-C ++ 5.11,以及IntelliJ IDEA IDE。
四、实验内容
1、厄拉多塞筛算法(Sieve of Eratosthenes)
(1)、算法原理
辅助变量 i 从 2 到 N的平方根 遍历,在 [2,N] 区间 当中将所有 i 的倍数删除,剩下的数即为 [2,N] 中的全部素数。
(2)、算法流程
本算法的大致流程如下图所示:
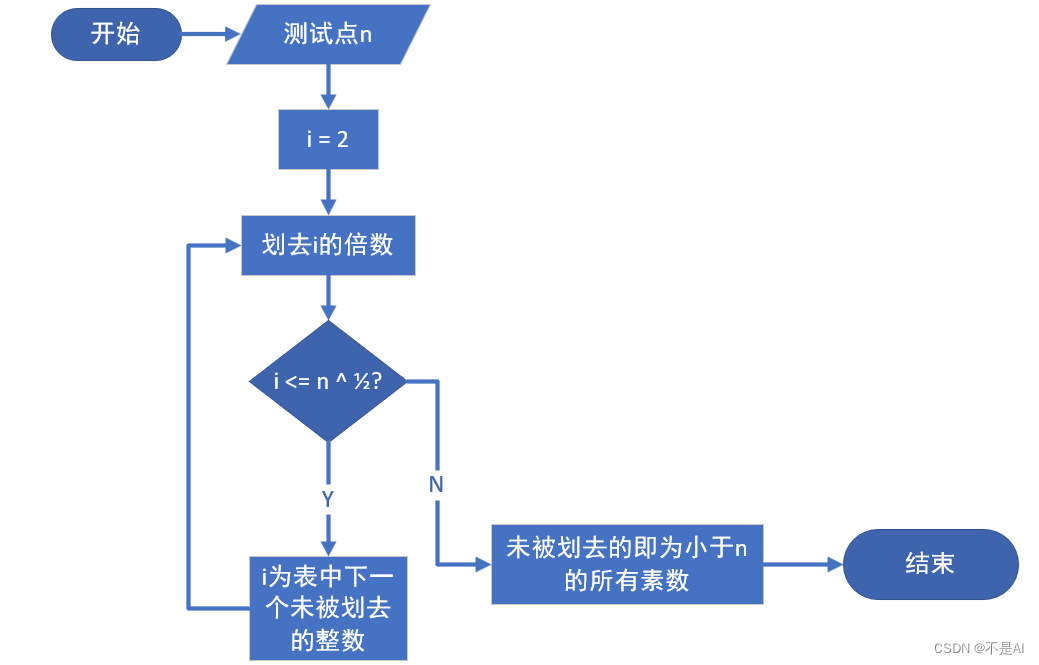
(3)、算法的代码实现(C语言)
#include <stdio.h>
#include <math.h>int flags[10010] = { 0 }; // 0代表质数,1代表合数
int isprime[10010] = { 0 }; // 质数的集合
int i, j;
int num; // [2,N]中质数的个数void getprimes(unsigned long long N);int main()
{unsigned long long N;printf("请输入N: ");scanf("%lld", &N);getprimes(N);return 0;
}void getprimes(unsigned long long N)
{for(i = 2;i < sqrt(N) + 1;i ++){if(flags[i] == 0){j = i * i; //从i的平方开始标记 while(j <= N){//将所有i的倍数(除i本身之外)标记为合数flags[j] = 1; j += i;}}}printf("[2,N]中的全部质数为:\n");for(i = 2;i <= N;i ++){if(flags[i] == 0) //若i为质数{num ++; printf("%d ", i);}}printf("\n");printf("共 %lld 个", num);
}
(4)、算法测试
测试点1:n = 2
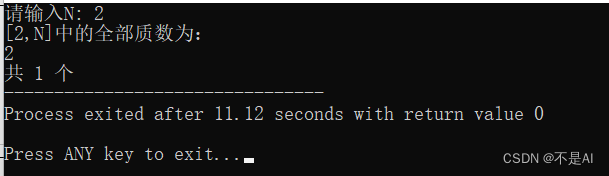
测试点2:n = 103:
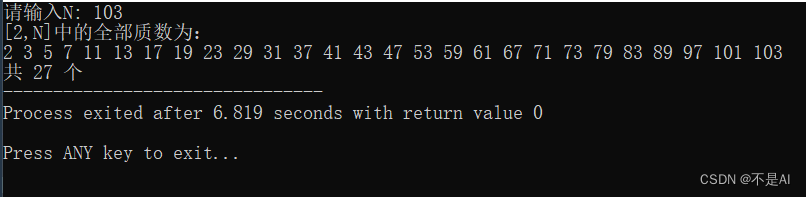
测试点3:n = 10000
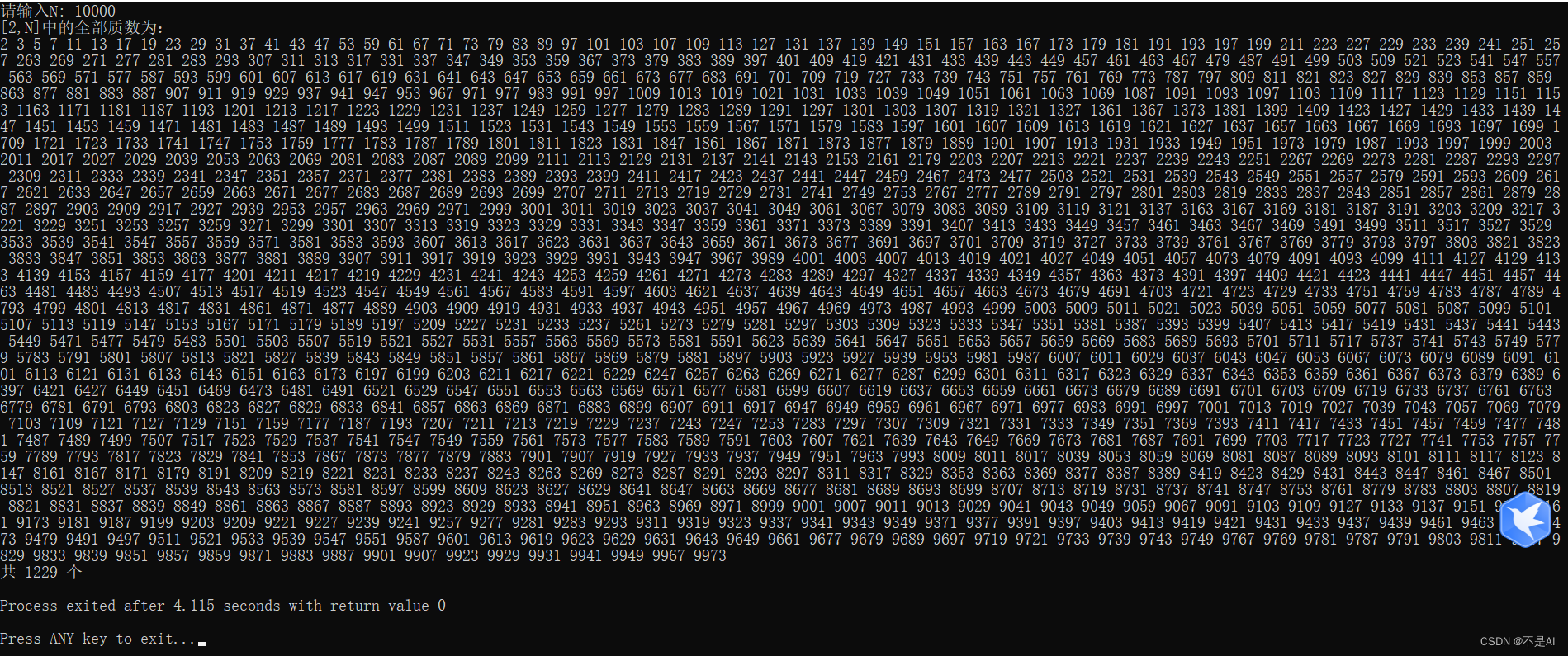
2、简单欧几里得算法(Simple Euclid’s Algorithm)
(1)、算法原理
简单欧几里得算法用于求2个整数a和b的最大公约数,该算法原理基于等式gcd(a,b)=gcd(b,a mod b),其中 gcd(a, b) 表示a和b的最大公约数,mod表示取模运算。
(2)、算法流程
本算法的大致流程如下图所示:
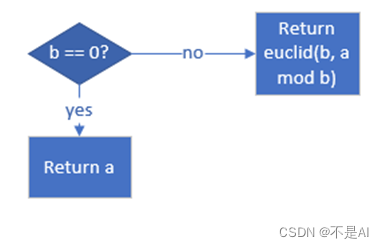
(3)、算法的代码实现(C语言)
#include <stdio.h>
#include <math.h>int getgcd(int a, int b);//求a和b的最大公因数int main(){int a, b;printf("请输入整数a: ");scanf("%d", &a);printf("请输入整数b: ");scanf("%d", &b);printf("%d 和 %d 的最大公约数是 %d", a, b, getgcd(a, b));return 0;
}int getgcd(int a, int b){if(b == 0){return abs(a);}else{return getgcd(b, a % b);}
}
(4)、算法测试
测试点1:a = 7, b = 5
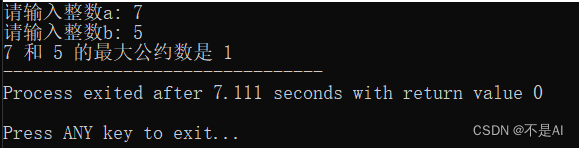
测试点2:a = 31, b = -13
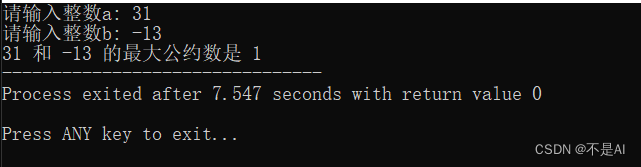
测试点3:a = 24, b = 36;
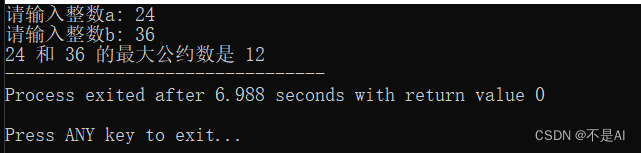
(5)大整数测试
测试算法在极大整数(位数远超出C语言中 unsigned long long 所能表示的范围)上的表现。使用 Java 语言中的大整数类 BigInteger实现。算法的完整代码如下:
import java.math.BigInteger;public class euclid {public static BigInteger euclidfunc(BigInteger a, BigInteger b){BigInteger zero;BigInteger tmp;zero = new BigInteger("0");while((b.compareTo(zero))!= 0) {tmp = a.mod(b);a = b;b = tmp;}if((b.compareTo(zero)) == 0) {return a;}return zero;}public static void main(String[] args) {BigInteger a, b;a = new BigInteger(""); // 以字符串的形式填入测试点a的数值b = new BigInteger(""); // 以字符串的形式填入测试点a的数值System.out.println("a 和 b 的最大公约数是:");System.out.println(euclidfunc(a, b));}
}
测试方面,选取2组互质的大整数,以及1组最大公约数为2的大偶数,作为测试用例,以验证算法对于大整数的正确性。
大整数测试点1:
a = 2461502723515673086658704256944912426065172925575,
b = 1720876577542770214811199308823476528929542231719
运行结果:
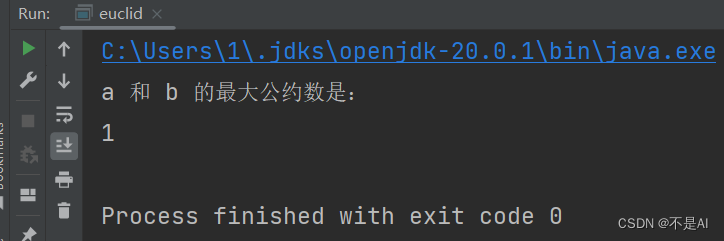 大整数测试点2:
大整数测试点2:
a = 137096164691449488835122291235023051763859318102840889067550902
3843189897270890443917889846802171079840187598665712521108447262149
9595371254346390738382042,
b = 192350399949876251675909634808997772559337752383120440971227732
5564753027680631763602672767980082537045932161772487151544214743242
0951257037823141069640181
运行结果:
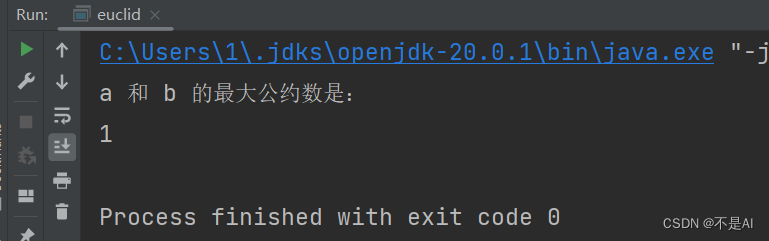 大整数测试点3:
大整数测试点3:
a = 965578072786402991215194630452063779349788872980869942115905155
7171732595578592378315943243630787051274235487747679004689180215305
3719263845602618422474671707896136814707875793300040916757228826108
4994903112959425534780109130436805236126554005262552907029834903821
91419067057726624348815391509161304477322782,
b = 146116799305702219220540123503890666704710410600856387071776221
5924772567527599977981699318091564264712437997953740725104236453636
8053733781377426865890713096999414678345169283722277214494143490905
0652825715582967684984814095461041109999161468223272534833391335036
612863782740784573110824091866969655931097032
运行结果:
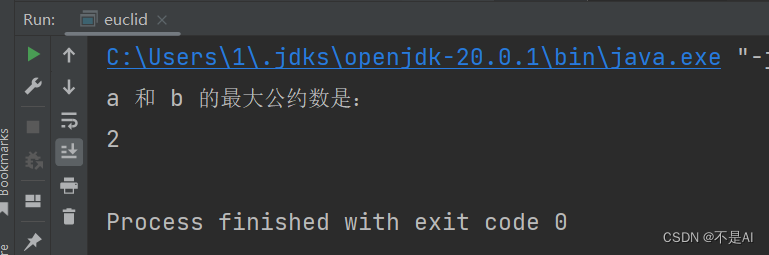
至此,本次实验结束。
五、参考文献
1、《密码编码学与网络安全——原理与实践(第七版)》(Cryptography and Network Security, Principles and Practice, Seventh Edition),【美】威廉 斯托林斯 William Stallings 著,王后珍等 译,北京,电子工业出版社,2017年12月。
2、《密码学实验教程》,郭华 刘建伟等 主编,北京,电子工业出版社,2021年1月。