【数据结构】堆的实现和排序

目录

1、堆的概念和结构

1.1、堆的概念

1.2、堆的性质

1.3、堆的逻辑结构和存储结构

2、堆的实现

2.1、堆的初始化和初始化

2.2、堆的插入和向上调整算法

2.3、堆的删除和向下调整算法

2.4、取堆顶的数据和数据个数

2.5、堆的判空和打印

2.6、测试

3、堆的应用

3.1、堆排序

3.1.1、建堆

3.1.2、排序

4、TOP-K问题

1、堆的概念和结构

1.1、堆的概念

简单理解堆是一个数组，可以把数组看成一个完全二叉树，根节点最大的堆是大根堆，根节点最小的堆是小根堆

1.2、堆的性质

堆中某个结点的值总是不大于或者不小于其父结点的值

（即树中所有的父亲都是<=孩子或者>=孩子）

堆是一棵完全二叉树

1.3、堆的逻辑结构和存储结构

堆的逻辑结构是一个完全二叉树，存储结构是数组

2、堆的实现

2.1、堆的初始化和初始化

void HeapInit(HP* php);
void HeapDestory(HP* php);//堆的初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;//扩容errorphp->size = php->capacity = 0;
}
//堆的销毁
void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}

2.2、堆的插入和向上调整算法

在堆尾插入数据后，在插入的位置开始向上调整，依然保持堆结构

void HeapPush(HP* php,HPDataType x);void AdjustUp(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){//扩容int NewCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HP* temp = (HP*)realloc(php->a,  NewCapacity*sizeof(HPDataType));if (temp == NULL){printf("realloc fail\n");exit(-1);}php->a = temp;php->capacity = NewCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);
}

2.3、堆的删除和向下调整算法

堆要删除一个数据，一般是删除堆顶的数据，如果直接删除堆顶的数据，那么堆的结构全部乱了，要重新建堆，时间复杂度高，并且没有用到堆的特性，具体做法是将堆顶的数据和堆尾的数据进行交换，再采用向下调整算法重新生成一个堆。

向下调整算法的前提是左右子树都是堆

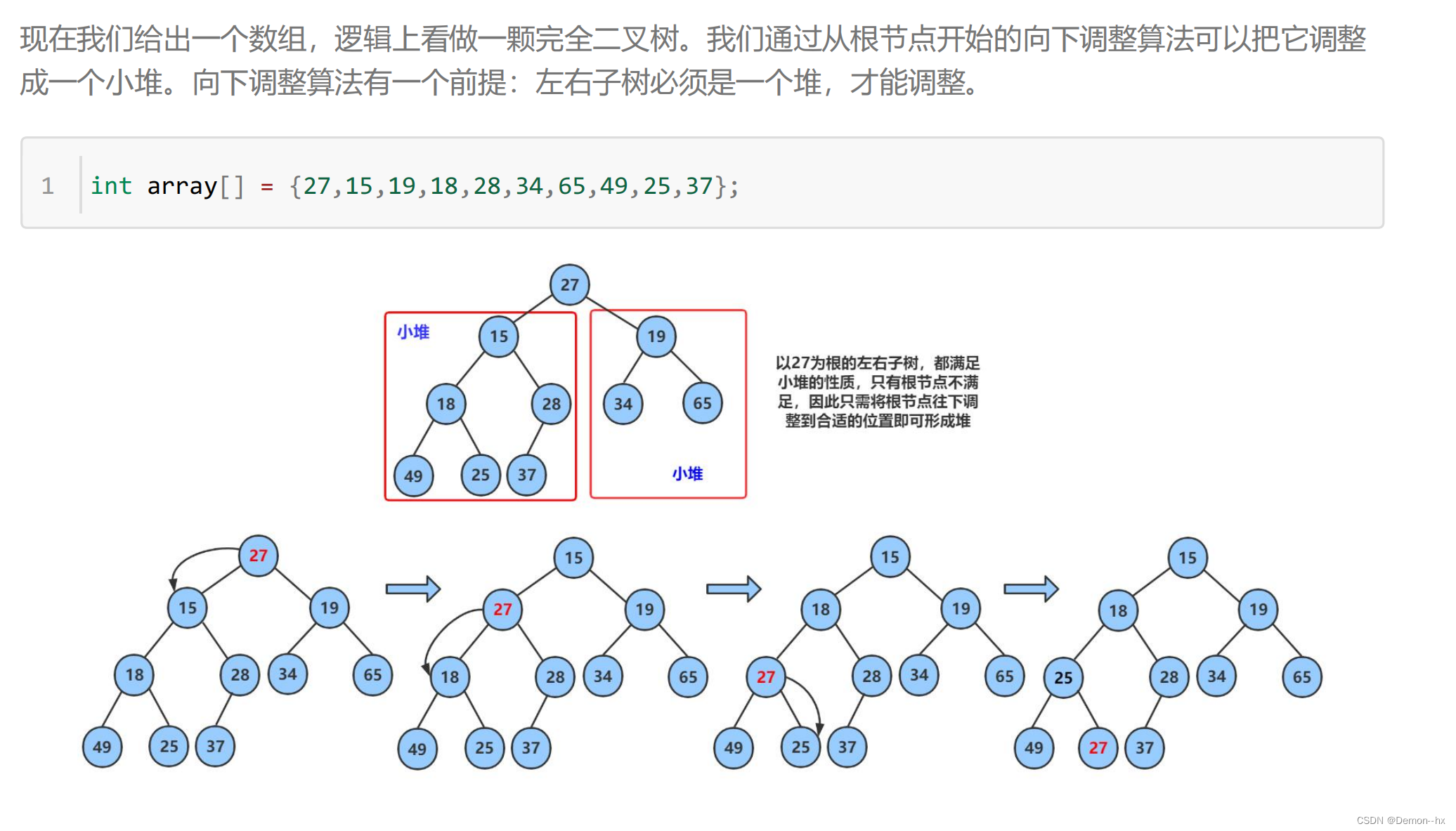
void HeapPop(HP* php);//     删除小堆堆顶的元素
//思路：选出左右孩子小的一个
//     小的孩子比父亲小，交换数据，继续向下调整，孩子如果比父亲大，调整结束
void AdjustDown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){
//右孩子下标要小于数组的范围sizeif (child + 1 < size && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}//删除堆里的数据 还要保持大小堆
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&(php->a[0]), &(php->a[php->size-1]));php->size--;AdjustDown(php->a, php->size, 0);
}

2.4、取堆顶的数据和数据个数

HPDataType HeapTop(HP* php);//取堆顶的数据
int HeapSize(HP* php);    //堆的数据个数HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(HP* php)
{assert(php);return php->size;
}

2.5、堆的判空和打印

bool HeapEmpty(HP* php);//堆的判空
void HeapPrint(HP* php);//堆的打印bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}void HeapInit(HP* php)
{assert(php);php->a = NULL;//扩容errorphp->size = php->capacity = 0;
}

2.6、测试

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"void HeapTest()
{HP hp;HeapInit(&hp);int a[] = { 27,15,19,18,28,34,65,49,25,37 };for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){HeapPush(&hp, a[i]);}printf("堆插入完成:");HeapPrint(&hp);//排升序 建小堆 将堆顶的数据回写到数组中//排降序 建大堆 将堆顶的数据回写到数组中int i = 0;while (!HeapEmpty(&hp)){//printf("%d ", HeapTop(&hp));//HeapPop(&hp);a[i++] = HeapTop(&hp);HeapPop(&hp);}printf("回写到数组的升序序列:");for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}printf("\n");
}
int main()
{HeapTest();
}//运行结果:
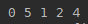
//堆插入完成:15 18 19 25 28 34 65 49 27 37
//回写到数组的升序序列:15 18 19 25 27 28 34 37 49 65

3、堆的应用

3.1、堆排序

3.1.1、建堆

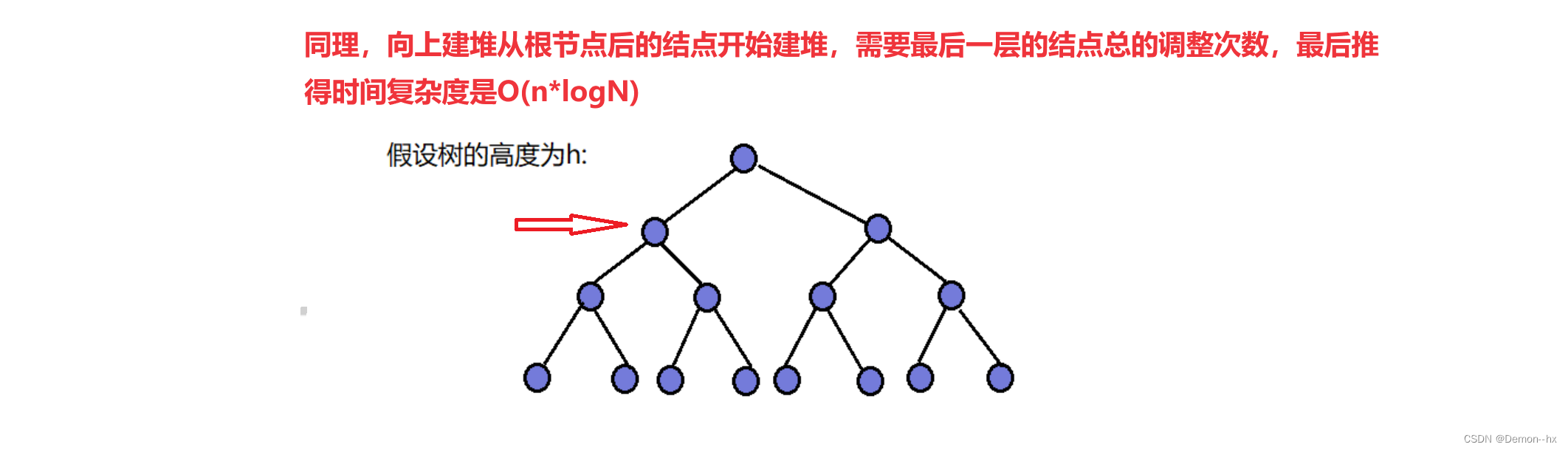
建堆有两种方式：向上建堆和向下建堆

向下建堆的时间复杂度是O(n)

向上建堆的时间复杂度是O(n*logN)

3.1.2、排序

建堆完成后，排升序，建大堆，排降序，建小堆

假设要排升序，需要建立大堆，将堆顶的数据和堆尾的数据交换，再用向下调整算法重新将次大的数排到堆顶位置，依次循环上述步骤，最后得到升序的序列

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2;i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
void HeapSortTest()
{int a[] = { 27,15,19,18,28,34,65,49,25,37 };HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}
}
int main()
{HeapSortTest();return 0;
}//输出结果 15 18 19 25 27 28 34 37 49 65

4、TOP-K问题

TOP-K问题：即求数据结合中前K个最大元素或者最小元素，一般情况下数据量都比较大。

思路1：堆排序 时间复杂度O(N*logN)

思路2：将这N个元素建成大堆， Top和Pop K次 时间复杂度 O(O(n)+k*logN);

假设有N个元素，N非常大，有100亿个元素，k比较小，为100，求找出N中的前100大的元素。

前面两种思路当数据量特别大时求解不太容易现实，100亿个整数要占用40G的内存(1G=1024MB=1024*1024kb=1024*1024*1024byte 1G占10亿字节左右)，明显不合适。

思路：

1、选取前K个数建小堆

2、剩下的N-K个数每次和小堆堆顶的数据比较，如果比堆顶的数据大，则交换堆顶的数据，比完后，最后堆里的K个数，就是最大的前K个数。

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#include<assert.h>
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//向下调整算法
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child+1<size&&a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2+1;}else{break;}}
}
void TopK(int* a, int n, int k)
{int* KMinHeap = (int*)malloc(sizeof(int) * k);assert(KMinHeap);//选出n中前k个数for (int i = 0; i < k; i++){KMinHeap[i] = a[i];}//对前k个数进行建堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(KMinHeap, k, i);}//n-k个数依次和堆顶数据进行交换for (int i = k; i < n; i++){if (a[i] > KMinHeap[0]){//Swap(&KMinHeap[0], &a[i]);KMinHeap[0] = a[i];AdjustDown(KMinHeap, k, 0);}}//打印前k大的数for (int i = 0; i < k; i++){printf("%d ", KMinHeap[i]);}printf("\n");
}
void TestTopK()
{int n = 10000;int* a = (int*)malloc(sizeof(int) * n);srand(time(0));for (int i = 0; i < n; i++){a[i] = rand() % 100000;}a[5] = 100000 + 1;a[1231] = 100000 + 2;a[531] = 100000 + 3;a[5121] = 100000 + 4;a[115] = 100000 + 5;a[2335] = 100000 + 6;a[9999] = 100000 + 7;a[76] = 100000 + 8;a[423] = 100000 + 9;a[3144] = 100000 + 10;TopK(a, n, 10);
}
int main()
{TestTopK();return 0;
}
//输出结果:100001 100002 100003 100004 100005 100007 100009 100006 100008 100010

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/412781.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

CentOS查看修改时间

CentOS查看修改时间

经常玩docker的朋友应该都知道&#xff0c;有很多的镜像运行起来后&#xff0c;发现容器里的系统时间不对&#xff0c;一般是晚被北京时间8个小时&#xff08;不一定&#xff09;。 这里合理怀疑是镜像给的初始时区是世界标准时间&#xff08;也叫协调世界时间&#xff09;。 有…
阅读更多...
CPU密集型计算、IO密集型计算、多进程、多线程

CPU密集型计算、IO密集型计算、多进程、多线程

参考链接&#xff1a; 使用多进程multiprocessing模块加速程序的运行_哔哩哔哩_bilibili 什么是CPU密集型计算、IO密集型计算&#xff1a; CPU密集型&#xff1a; CPU密集型也叫计算密集型&#xff0c;是指I/O在很短的时间就可以完成&#xff0c;CPU需要大量的计算和处理&a…
阅读更多...
44.5K Star，简单易用自动化运维监控工具

44.5K Star，简单易用自动化运维监控工具

Hi&#xff0c;骚年&#xff0c;我是大 G&#xff0c;公众号「GitHub指北」会推荐 GitHub 上有趣有用的项目&#xff0c;一分钟 get 一个优秀的开源项目&#xff0c;挖掘开源的价值&#xff0c;欢迎关注。 今天介绍一个开源的自动化运维监控工具&#xff0c;它是一个轻量的开源…
阅读更多...
【征服redis1】基础数据类型详解和应用案例

【征服redis1】基础数据类型详解和应用案例

博客计划 &#xff0c;我们从redis开始&#xff0c;主要是因为这一块内容的重要性不亚于数据库&#xff0c;但是很多人往往对redis的问题感到陌生&#xff0c;所以我们先来研究一下。 本篇&#xff0c;我们先看一下redis的基础数据类型详解和应用案例。 1.redis概述 以mysql为…
阅读更多...
Linux编译器--gcc和g++使用

Linux编译器--gcc和g++使用

gcc和g使用 一、gcc/g的作用1.1 预处理1.2 编译1.3 汇编1.4 链接 二、静态库和动态库三、make/Makefile3.1 make/Makefile3.2 依赖关系和依赖方法3.3 多文件编译3.4 make原理3.5 项目清理 四、linux下的第一个小程序-进度条4.1 行缓冲区的概念4.2 \r和\n4.3 进度条代码 一、gcc…
阅读更多...
Verilog刷题笔记15

Verilog刷题笔记15

题目&#xff1a; An adder-subtractor can be built from an adder by optionally negating one of the inputs, which is equivalent to inverting the input then adding 1. The net result is a circuit that can do two operations: (a b 0) and (a ~b 1). See Wikipe…
阅读更多...
Java数据结构之图(头歌平台，详细注释)

Java数据结构之图(头歌平台，详细注释)

第1关&#xff1a;图的表示 任务描述 图&#xff08;Graph&#xff09;是表示一些事物或者状态的关系的表达方法。由于许多问题都可以归约为图的问题&#xff0c;人们提出了许多和图相关的算法。 本关任务&#xff1a;学习图的相关概念和表示&#xff0c;并用邻接表示图。 相关…
阅读更多...
刷题总结1.18 下午 （堆）

刷题总结1.18 下午 （堆）

关联数组”是一种具有特殊索引方式的数组。不仅可以通过整数来索引它&#xff0c;还可以使用字符串或者其他类型的值&#xff08;除了NULL&#xff09;来索引它。 关联数组和数组类似&#xff0c;由以名称作为键的字段和方法组成。 它包含标量数据&#xff0c;可用索引值来单独…
阅读更多...
虚拟化网络

虚拟化网络

vm1和vm2通过虚拟交换机与主机进行交换&#xff0c; 虚拟交换机&#xff1a;&#xff08;通过软件虚拟出来的交换机&#xff09; 1、LinuxBridge虚拟交换机 2、OVS&#xff08;Open Virtual Switch&#xff09;虚拟交换机 虚拟机的传输是通过虚拟交换机&#xff0c;然后连到…
阅读更多...
如何判断光模块失效以及光模块应用注意点

如何判断光模块失效以及光模块应用注意点

1.测试光功率是否在指标要求范围之内&#xff0c;如果出现无光或者光功率小的现象&#xff0c;处理方法: A、检查光功率选择的波长和测量单位 (dbm)。 B、清洁光纤连接器端面&#xff0c;光模块光口。 C、检查光纤连接器端面是否发黑和划伤&#xff0c;光纤连接器是否存在折断&…
阅读更多...
Jenkins之pipeline

Jenkins之pipeline

安装插件 Pipeline Pipeline: Stage View Plugin 创建任务 配置 demo 开始实践 拉取git仓库代码 checkout scmGit(branches: [[name: */main]], extensions: [], userRemoteConfigs: [[url: http://178.119.30.133:8929/root/mytest.git]])通过SonarQube做质量检测 sh …
阅读更多...
一键式Excel分词统计工具：如何轻松打包Python脚本为EXE

一键式Excel分词统计工具：如何轻松打包Python脚本为EXE

一键式Excel分词统计工具&#xff1a;如何轻松打包Python脚本为EXE 写在最前面需求分析直接用Python打包为什么大&#xff1f;为什么要使用conda环境&#xff1f; 将Python脚本打包为一个独立的应用程序1. 编写Python脚本&#xff1a;初步功能实现2. 初步图形用户界面&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023