个人主页 : zxctsclrjjjcph
文章封面来自:艺术家–贤海林
如有转载请先通知
目录
- 1. 前言
- 2. 归并排序
- 2.1 递归实现
- 2.1.1 分析
- 2.1.2 代码实现
- 2.2 非递归实现
- 2.2.1 分析
- 2.2.2 代码实现
- 3. 计数排序
- 3.1 分析
- 3.2 代码实现
- 4. 附代码
- 4.1 Sort.h
- 4.2 Sort.c
- 4.3 Test.c
1. 前言
在前面的文章中介绍了 插入排序和交换排序,今天来分享的是归并排序和计数排序。
话不多说,正文开始。
2. 归并排序
归并排序既是内排序也是外排序。
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
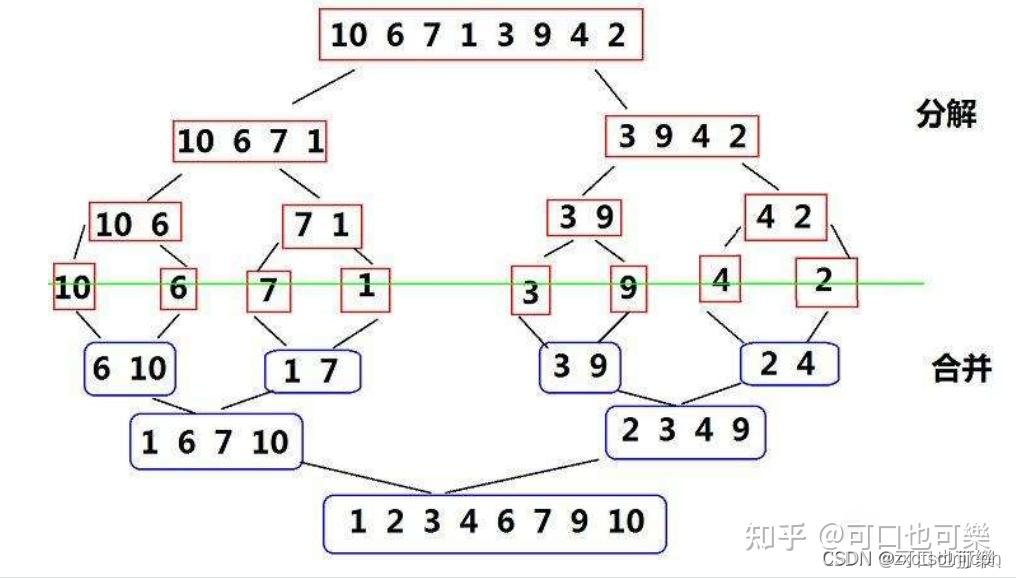

归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
2.1 递归实现
2.1.1 分析
左边和右边都无序,先分割,8个分为4个,4个分为两个,两个分为1个,一个可以认为它有序了。
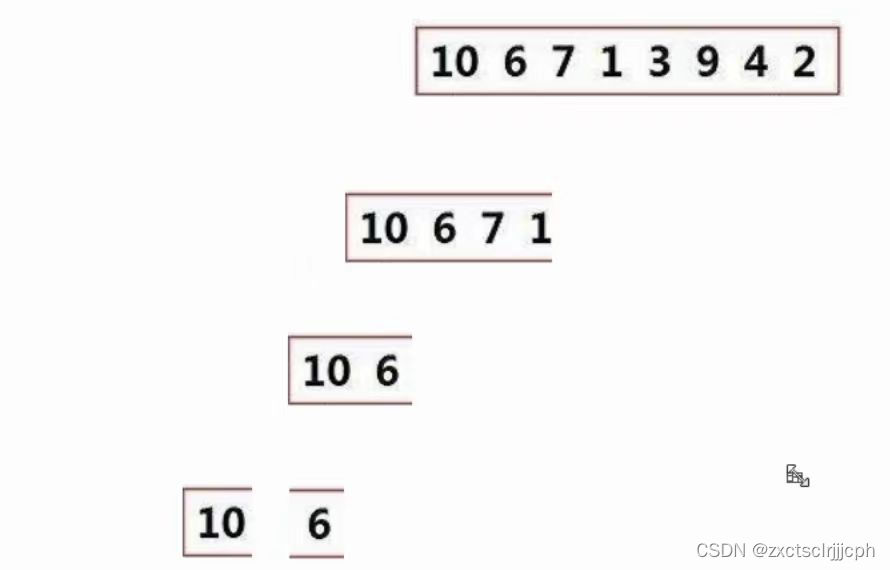
一个和一个归为2个有序,2个和2个归为4个有序,4个4个归为有序。这里用的就是后序递归。
用一个临时数组tmp来进行排序后再拷贝回原数组,不可能每次调用数组自己就再开辟一次空间。
在递归的时候必须是一段区间,所以这里重新写一个子函数_MergeSort()来实现递归。
直接分割区间mid = (begin + end) / 2,然后分割左区间再分割右区间,当只有一个值时,已经有序了。

归并时,将左右区间里面的值进行比较,取小的尾插在tmp临时数组中。一个一个插入,最后肯定还剩下一组,如果剩下第一个区间就直接尾插tmp[i++] = a[begin1++];同样剩下第二个区间也直接尾插tmp[i++] = a[begin2++],最后拷贝回原数组memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1))。
2.1.2 代码实现
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid][mid+1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// [begin, mid][mid+1, end]归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}来个例子测试一下。
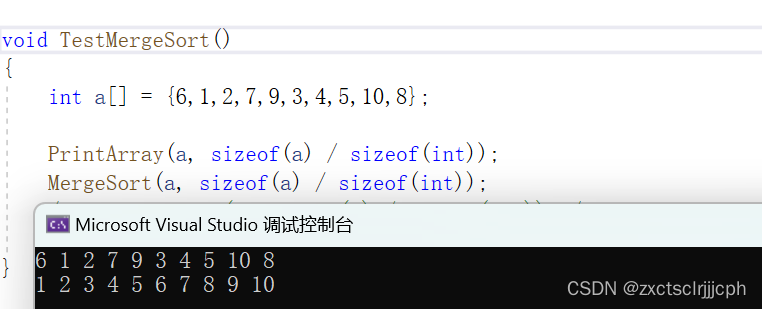
2.2 非递归实现
如果用栈模拟实现,是不合适的,栈适合前序遍历,而归并排序是后序遍历。可以在栈里面对区间进行分割,但是栈空了,已经没有区间了,实现不了归并。
2.2.1 分析
归并分割是为了实现有序,直接到过来,一个和一个归并就实现有序。
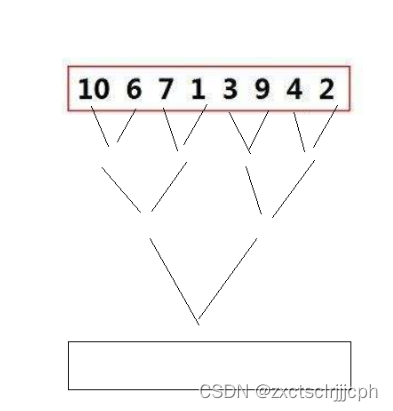
同样要先开一个临时数组tmp,先归第一组区间[begin1, end1][begin2, end2]实现归并,谁小谁尾插,归并逻辑和上面递归是一样的。
gap为每一组数据个数,第一个区间就是int begin1 = i, end1 = i + gap - 1;
第二个区间就是int begin2 = i + gap, end2 = i + 2 * gap - 1。(这里算的是下标,所以end得减1)。
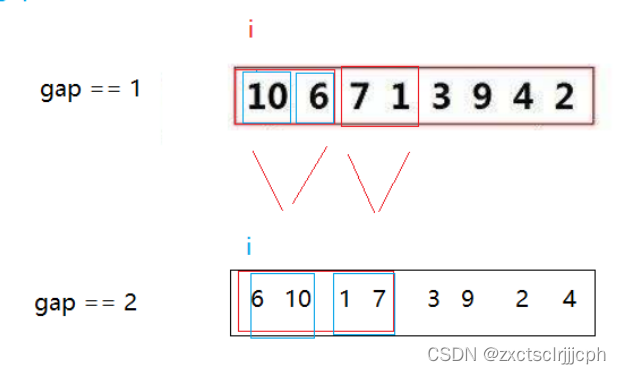
这里实现完一组gap,要实现下一个gap,用一个for 循环实现for(size_t i = 0; i < n; i += 2 * gap)。那么结束条件就是gap > n。

代码写出来就是
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){printf("gap:%2d->", gap);for (size_t i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1][begin2, end2] 归并printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * 2 * gap);}printf("\n");gap *= 2;}free(tmp);
}
举个例子实现代码,发现结果出不来。为什么呢?

说明区间越界了,得对区间进行处理。
区间[begin1, end1][begin2, end2]中begin1不存在越界,i是一直小于n。
end1,begin2, end2都会存在越界情况。
对end1如果它大于n,不需要归并了,就直接break;
对begin2如果它大于n,说明第二个区间越界了,也不需要归并,就直接break;
对end2如果它大于n,这里的第二个区间还存在一些值,将区间修改为n-1(end2 = n - 1)。
if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}

这里得注意拷贝,在使用memcpy时,归一组就拷贝一组,如果全部归并之后再拷贝,就会出现随机值。
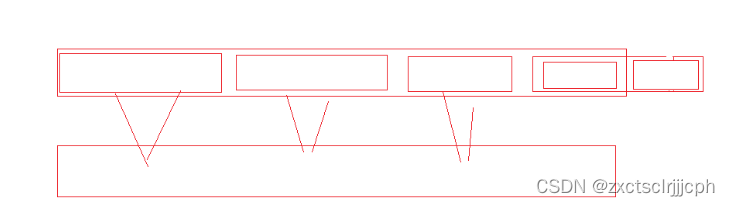
放在外面,如果后面区间出现越界,直接break,就没有就行归并,它本身就是有序的,会把之前有序的数据覆盖。
2.2.2 代码实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){printf("gap:%2d->", gap);for (size_t i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1][begin2, end2] 归并// 边界的处理if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}printf("\n");gap *= 2;}free(tmp);
}
举个例子:
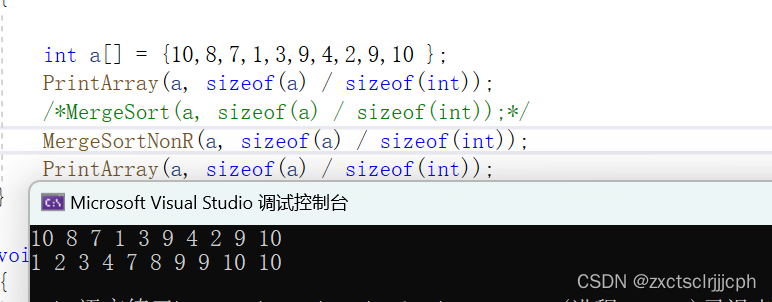
3. 计数排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中

计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(countN范围)
- 稳定性:稳定
局限性:
- 不适合分散的数据,更适合集中数据;
- 不适合浮点数、字符串、结构体数据排序,只适合整数。
3.1 分析

代码核心就是:

a[i]是多少就对多少进行计数,出现几次就加几次。
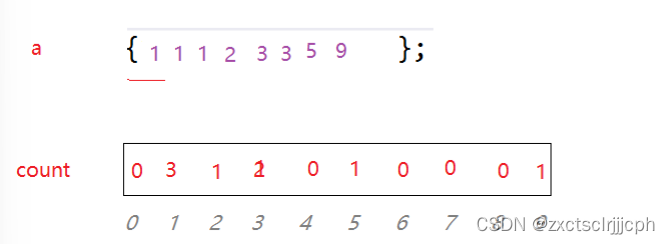
1这个位置出现3次就在原数组中写3个1,2的位置出现一次就在原数组中写一个2。

这里不可能每一次都从0开始进行排序,每一次都是几对于几
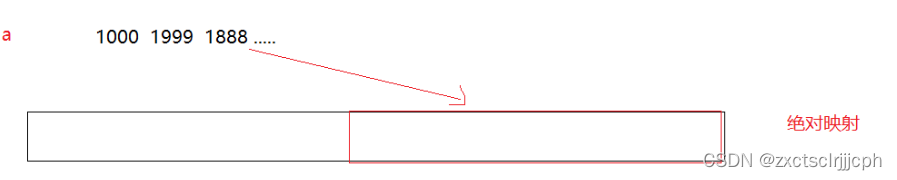
如果是这样,那么就浪费了1000个空间。
这里使用相对映射而不是绝对映射。

找最小值1000,最大值1999。
然后用calloc开一个计数数组,因为calloc会初始化为0。
这里1000就在0的位置,1999就在999的位置。
统计次数:对相对映射位置进计数。
for (int i = 0; i < n; i++){count[a[i] - min]++;}
这里怎么还原呢?
加回去就行j + min。
后置减减,返回的减减之前的值,往回写。
for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}
这里负数也能使用计数排序。
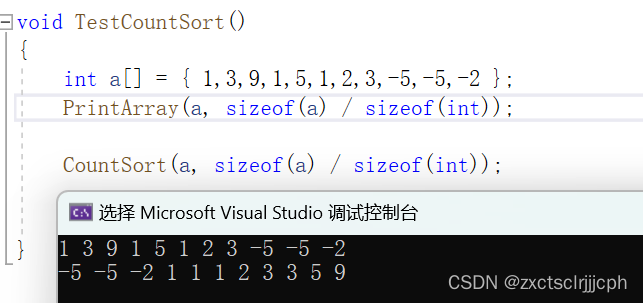
3.2 代码实现
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){printf("calloc fail\n");return;}// 统计次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int i = 0;for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}
}
4. 附代码
4.1 Sort.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>void PrintArray(int* a, int n);void MergeSort(int* a, int n);
void MergeSortNonR(int* a, int n);
void CountSort(int* a, int n);
4.2 Sort.c
#include"Sort.h"void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid][mid+1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// [begin, mid][mid+1, end]归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){/*printf("gap:%2d->", gap);*/for (size_t i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1][begin2, end2] 归并/*printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);*/// 边界的处理if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}/*printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);*/int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}/*printf("\n");*/gap *= 2;}free(tmp);
}// 基数排序/桶排序// 计数排序
// 时间:O(N+range)
// 空间:O(range)
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){printf("calloc fail\n");return;}// 统计次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int i = 0;for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}
}
4.3 Test.c
#include"Sort.h"void TestMergeSort()
{int a[] = {10,8,7,1,3,9,4,2,9,10 };PrintArray(a, sizeof(a) / sizeof(int));/*MergeSort(a, sizeof(a) / sizeof(int));*/MergeSortNonR(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestCountSort()
{int a[] = { 1,3,9,1,5,1,2,3,-5,-5,-2 };PrintArray(a, sizeof(a) / sizeof(int));CountSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{/*TestMergeSort();*/TestCountSort();return 0;
}
有问题请指出,大家一起进步!

![[论文阅读]DeepFusion](https://img-blog.csdnimg.cn/direct/7aea0198a8a6438c84b14e0fb4ff44b6.png)