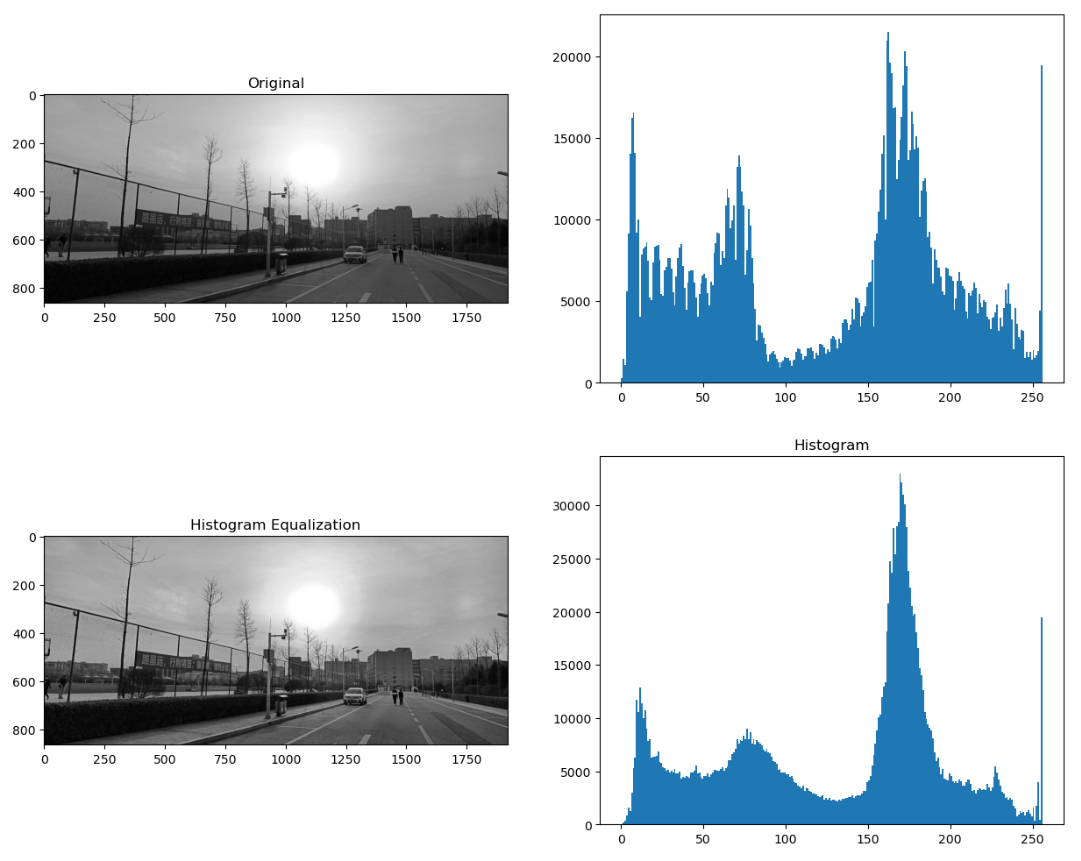
一.代数证明
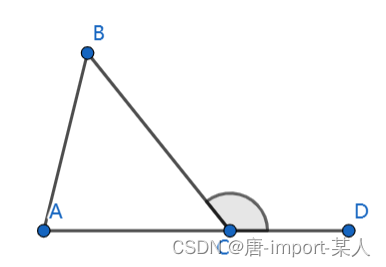
∵ 对与△ A C B 中 ∠ c 外接三角形是 ∠ B C D ∵对与△ACB中∠c外接三角形是∠BCD ∵对与△ACB中∠c外接三角形是∠BCD
∴ ∠ B C D = π − ∠ C ∴∠BCD=\pi-∠C ∴∠BCD=π−∠C
∵ ∠ A + ∠ B + ∠ C = π ∵∠A+∠B+∠C=\pi ∵∠A+∠B+∠C=π
∴ ∠ B C D = ∠ A + ∠ B ∴∠BCD=∠A+∠B ∴∠BCD=∠A+∠B
∴ ∠ B C D > ∠ A ∧ ∠ B C D > ∠ B ∴∠BCD>∠A∧∠BCD>∠B ∴∠BCD>∠A∧∠BCD>∠B
二.几何证明
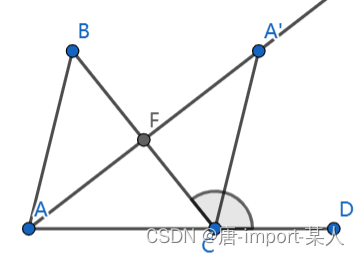
在△ABC做边BC的中点F,连接AF做角平分线,找到A于F的对称点 A ′ A' A′,连接 A ′ C A'C A′C
∵ A F = A ′ F , B F = C F , ∠ B F A = ∠ C F A ′ ∵AF=A'F,BF=CF,∠BFA=∠CFA' ∵AF=A′F,BF=CF,∠BFA=∠CFA′
∴ △ B F A ≌△ A ′ F C ∴△BFA≌△A'FC ∴△BFA≌△A′FC
∴ ∠ B = ∠ F C A ′ ∴∠B=∠FCA' ∴∠B=∠FCA′
∵ ∠ F C A ′ 在 ∠ F C D 内 ∵∠FCA'在∠FCD内 ∵∠FCA′在∠FCD内
所以 ∠ F C D > ∠ B 所以∠FCD>∠B 所以∠FCD>∠B
∵ ∠ A + ∠ B = π − ∠ B C A = ∠ D C F , ∧ ∠ A + ∠ B < π 2 ∵∠A+∠B=\pi-∠BCA=∠DCF,∧∠A+∠B<\frac{\pi}{2} ∵∠A+∠B=π−∠BCA=∠DCF,∧∠A+∠B<2π
∴ ∠ A < π 2 − ∠ B ∴∠A<\frac{\pi}{2}-∠B ∴∠A<2π−∠B
∴ ∠ A < π 2 − π + ∠ B C A ∴∠A<\frac{\pi}{2}-\pi+∠BCA ∴∠A<2π−π+∠BCA
∴ ∠ A + π 2 < ∠ B C A ∴∠A+\frac{\pi}{2}<∠BCA ∴∠A+2π<∠BCA
∴ ∠ B C A > ∠ A ∴∠BCA>∠A ∴∠BCA>∠A