题目1:654 最大二叉树
题目链接:654 最大二叉树
题意
根据不重复的整数数组nums构建最大的二叉树 ,根节点是数组中的最大值,最大值左边的子数组构建左子树,最大值右边的子数组构建右子树
nums数组中最少含有1个元素,并且nums中的元素数值均大于等于0
递归
递归三部曲:
1)确定递归函数的参数和返回值
2)确定终止条件
3)确定单层递归逻辑
数组

代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {//终止条件 因为递归的时候左数组可能为空,右数组可能为空if(nums.size()==0) return NULL;//单层递归逻辑//寻找中节点//找寻切割数组的位置int maxvalue = 0;int index = 0;for(int i=0;i<nums.size();i++){if(nums[i]>maxvalue){maxvalue = nums[i];index = i;}}int rootvalue = maxvalue;TreeNode* root = new TreeNode(rootvalue);//叶子节点if(nums.size()==1) return root;//切割数组 左闭右开vector<int> leftnums(nums.begin(),nums.begin()+index);vector<int> rightnums(nums.begin()+index+1,nums.end());root->left = constructMaximumBinaryTree(leftnums);root->right = constructMaximumBinaryTree(rightnums);return root;}
};下标
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* traversal(vector<int>& nums,int left,int right){//终止条件if(left>=right) return NULL;//单层递归逻辑//中节点int maxvalue = 0;int index = left;for(int i=left;i<right;i++){if(nums[i]>maxvalue){maxvalue = nums[i];index = i;}}TreeNode* root = new TreeNode(maxvalue);if(right - left == 1) return root;//左闭右开root->left = traversal(nums, left, index);//左闭右开root->right = traversal(nums, index+1, right);return root;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {return traversal(nums,0,nums.size());}
};题目2:617 合并二叉树
题目链接:617 合并二叉树
题意
两棵树相同位置的节点视为重叠,如果两棵树的两个节点重叠,将这两个节点的值相加作为新节点的值,若不重叠,则将不是NULL的节点作为新的节点,从而合成一颗新二叉树。
同时遍历两颗树的相同位置
递归
递归三部曲:
1)确定递归函数的参数和返回值
2)确定终止条件
3)确定单层递归逻辑

代码(返回改变后的root1)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {//终止条件if(root1==NULL) return root2;if(root2==NULL) return root1;//单层递归逻辑root1->val += root2->val;//中root1->left = mergeTrees(root1->left,root2->left);//左root1->right = mergeTrees(root1->right,root2->right);//右return root1;}
};代码(新root)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {//终止条件if(root1==NULL) return root2;if(root2==NULL) return root1;//单层递归逻辑TreeNode* root = new TreeNode(0);root->val = root1->val += root2->val;//中root->left = mergeTrees(root1->left,root2->left);//左root->right = mergeTrees(root1->right,root2->right);//右return root;}
};层序遍历
注意开始写 遇到NULL时的return 的情况
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {queue<TreeNode*> que;//这里不应该这么写,可能root1==NULL root2!=NULL 这时应该返回root2// if(root1!=NULL) que.push(root1);// if(root2!=NULL) que.push(root2);if(root1==NULL) return root2;if(root2==NULL) return root1;que.push(root1);que.push(root2);while(!que.empty()){TreeNode* node1 = que.front();que.pop();TreeNode* node2 = que.front();que.pop();node1->val += node2->val;if(node1->left!=NULL && node2->left!=NULL){que.push(node1->left);que.push(node2->left);}if(node1->right!=NULL && node2->right!=NULL){que.push(node1->right);que.push(node2->right);}if(node1->left==NULL && node2->left!=NULL) node1->left = node2->left;if(node1->right==NULL && node2->right!=NULL) node1->right = node2->right;}return root1;}
};题目3:700 二叉搜索树中的搜索
题目链接:700 二叉搜索树中的搜索
题意
在二叉搜索树中找到等值于val的节点,返回以该节点为根的子树,若不存在,则返回NULL
注意:二叉搜索树是有序的(左子树的值小于中节点的值,右子树的值均大于中节点的值),遍历二叉树,如果节点值小于val,说明要去该节点的右子树寻找;如果节点值大于val,说明要去该节点的的左子树寻找,如此递归下去
递归
递归三部曲
1)确定递归函数的返回值和参数
2)确定终止条件
3)确定单层递归逻辑 按照二叉搜索树的特性作为顺序去遍历,不用考虑前序,中序和后序了
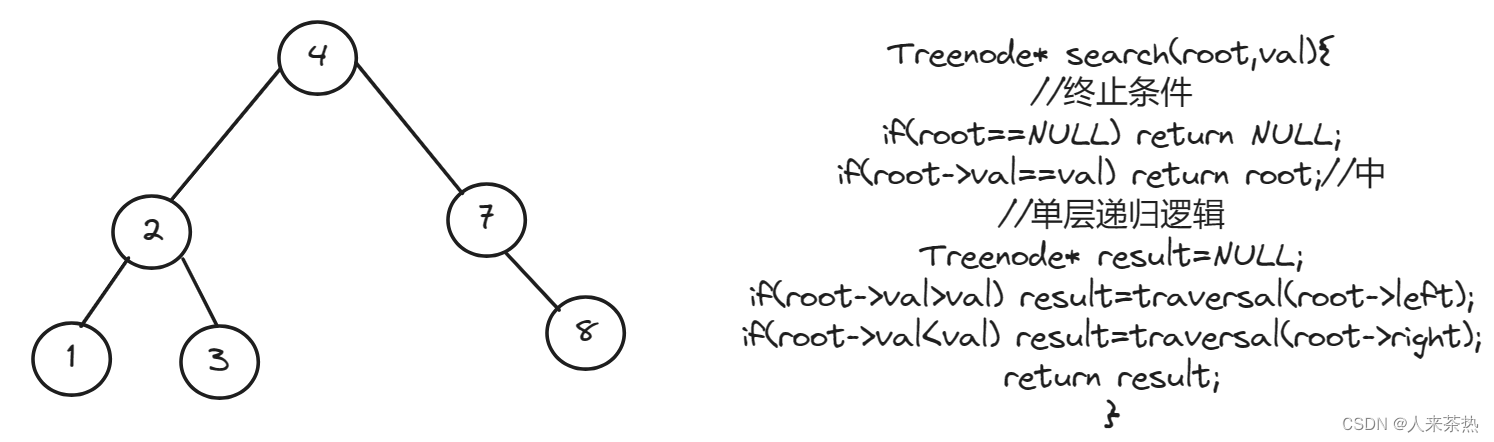
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {//终止条件if(root==NULL) return NULL;if(root->val==val) return root;//单层递归逻辑TreeNode* result;if(root->val>val) result = searchBST(root->left,val);if(root->val<val) result = searchBST(root->right,val);return result;}
};迭代法(极其简单)
不用使用栈,不需要回溯过程,因为二叉搜索树的节点数值的性质帮我们确定了搜索顺序
伪代码

代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {while(root!=NULL){if(root->val>val) root = root->left;else if(root->val<val) root = root->right;else return root;}return NULL;}
};题目4:98 验证二叉搜索树
题目链接:98 验证二叉搜索树
题意
判断一颗二叉树是否为有效的二叉搜索树,有效的二叉搜索树定义为:
1)节点的左子树的元素值均小于该节点
2)节点的右子树的元素值均大于该节点
3)左右节点的左右子树也为二叉搜索树
递归
递归三部曲:
1)确定递归函数的参数和返回值
2)确定终止条件
3)确定单层递归逻辑
数组
将二叉树中的每个元素按照中序遍历(左中右)的顺序,放入到数组中,然后判断数组是否是单调递增的即可
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> vec;void traversal(TreeNode* root){//终止条件if(root==NULL) return;//单层递归逻辑//中序遍历(左中右)traversal(root->left);vec.push_back(root->val);traversal(root->right);}bool isValidBST(TreeNode* root) {traversal(root);for(int i=0;i<vec.size();i++){if(i>=1 && vec[i]<=vec[i-1]) return false;}return true;}
};直接判断数组是否有序(初始化最大值)
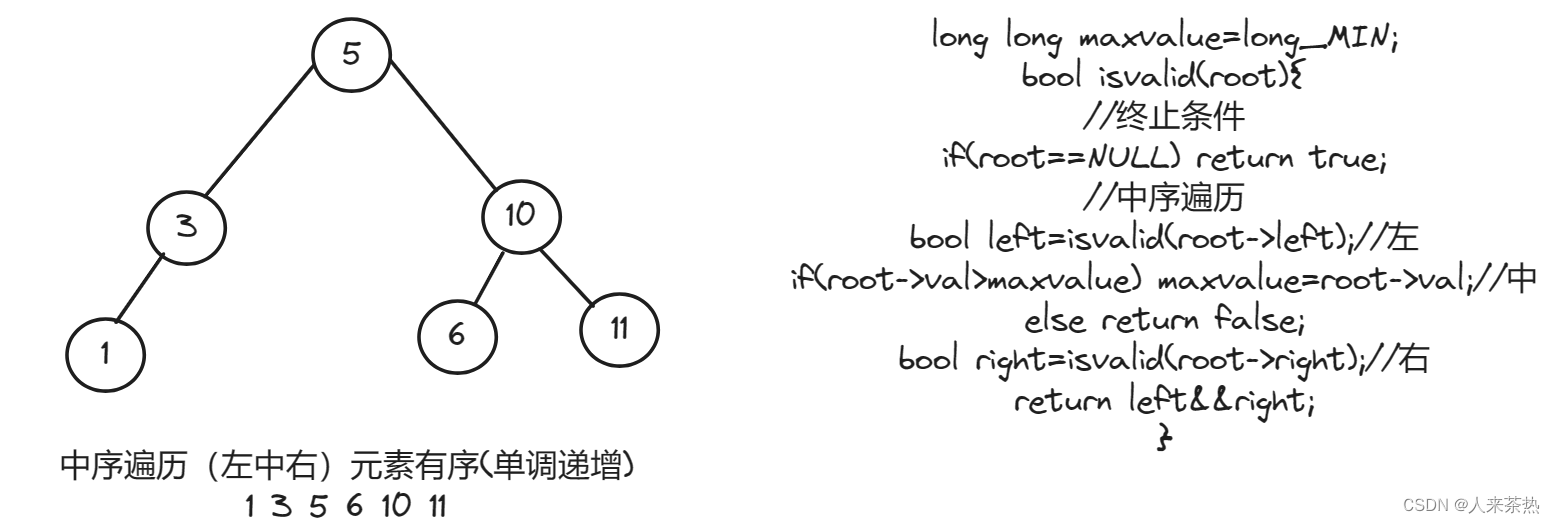
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:long long maxvalue = LONG_MIN;bool isValidBST(TreeNode* root) {//终止条件if(root==NULL) return true;//单层递归逻辑//中序遍历,左中右bool left = isValidBST(root->left);//左if(maxvalue<root->val) maxvalue = root->val;//中else return false;bool right = isValidBST(root->right);//右return left && right;}
};双指针优化(避免初始化最小值)
使用1个指针pre指向当前遍历节点的前一个节点,比较pre->val和root->val的大小
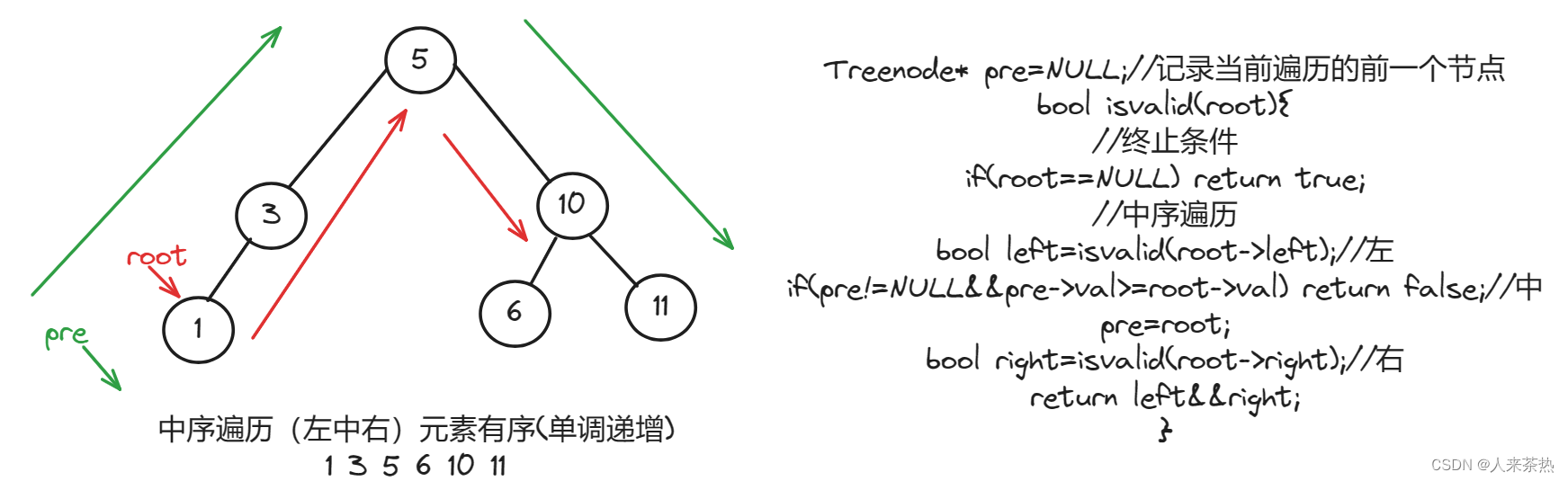
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pre = NULL;bool isValidBST(TreeNode* root) {//终止条件if(root==NULL) return true;//单层递归逻辑//中序遍历,左中右bool left = isValidBST(root->left);//左if(pre!=NULL && pre->val>=root->val) return false;//中pre = root;bool right = isValidBST(root->right);//右return left && right;}
};