目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1小波变换基础
4.2 多普勒效应与多普勒变换
4.3 小波多普勒变换
4.4 回波信号检测
5.算法完整程序工程
1.算法运行效果图预览


2.算法运行软件版本
matlab2022a
3.部分核心程序
%回波信号
for i = 1:length(hsearch)for j = 1:length(vsearch)hh = hsearch(i);vv = vsearch(j);tao1 = 2*sqrt(h^2 + v^2*t0^2)/c;tao2 = 2*sqrt(hh^2 + vv^2*t0^2)/c;ss2 = [];for k = 1:length(t)%%回波信号A = exp(-(t(k)-t0)^2/2/Dt^2);s0(k) = A*exp(sqrt(-1)*2*pi*(1 - 2*v^2*(t(k)-t0)/(c*sqrt(h^2 + v^2*(t(k)-t0)^2) + v^2*(t(k)-t0)) )*f0*(t(k)-tao1));%主动Dopplerlet变换d0(k) = exp(-(t(k)-t0)^2/2/Dt^2)*exp(sqrt(-1)*2*pi*(1 - 2*vv^2*(t(k)-t0)/(c*sqrt(hh^2 + vv^2*(t(k)-t0)^2) + vv^2*(t(k)-t0)) )*f0*(t(k)-tao2)); ends = awgn(s0,SNR,'measured');%回波过信道for k = 1:length(t)if abs(real(s0(k))-real(d0(k)))<=1e-8 & abs(imag(s0(k))-imag(d0(k)))<=1e-8ss2(k) = 1; elsess2(k) = s(k).*conj(d0(k)); endendxy(i,j)= mean(abs(ss2));end
end
17_014m4.算法理论概述
在雷达、声纳、无线通信等领域,回波信号检测是一项关键技术。传统的回波信号处理方法,如傅里叶变换,对于非平稳信号的处理能力有限。近年来,基于小波多普勒变换的回波信号检测方法因其优越的时频分析能力而受到广泛关注。该方法结合了小波变换和多普勒变换的特点,能够在时域和频域同时提供高分辨率的分析,从而有效地检测和处理复杂的回波信号。
4.1小波变换基础
小波变换是一种时频分析方法,它克服了傅里叶变换在处理非平稳信号时的局限性。小波变换通过将信号分解为一系列小波基函数的线性组合,能够在不同尺度上分析信号的局部特性。

在实际应用中,通常使用离散小波变换(DWT),其形式为:
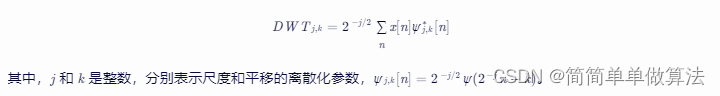
4.2 多普勒效应与多普勒变换
多普勒效应是指观测到的波频率与实际波源频率之间的差异,这种差异是由于波源和观测者之间的相对运动引起的。在雷达回波信号中,多普勒效应表现为回波信号的频率随时间的变化。
多普勒变换是一种将时域信号转换为多普勒频域的方法。对于单频信号 s(t)=Aexp(j2πf0t),其多普勒变换为:
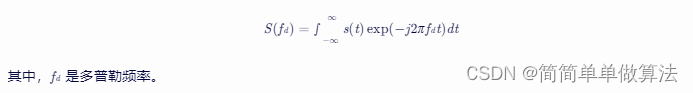
4.3 小波多普勒变换
小波多普勒变换(WDT)结合了小波变换和多普勒变换的特点,能够在时频域提供高分辨率的分析。其基本思想是将信号首先进行小波变换,然后在每个尺度上进行多普勒分析。
给定信号 x(t),其小波多普勒变换可以表示为:
其中,CWT(a,b) 是信号 x(t) 在尺度 a、平移 b 处的连续小波变换系数。
通过小波多普勒变换,我们可以得到信号在不同尺度下的多普勒频率分布,从而有效地检测和处理复杂的回波信号。
4.4 回波信号检测
基于小波多普勒变换的回波信号检测主要包括以下步骤:
-
信号预处理:对接收到的原始信号进行滤波、去噪等预处理操作,以提高后续处理的准确性。
-
小波变换:对预处理后的信号进行小波变换,得到信号在不同尺度下的时频表示。
-
多普勒分析:在每个尺度上进行多普勒分析,提取信号的多普勒频率信息。
-
特征提取:根据实际应用需求,从小波多普勒变换的结果中提取出有用的特征,如多普勒频率、幅度等。
-
信号检测与识别:利用提取的特征进行信号检测与识别,判断是否存在回波信号,并识别其类型。
5.算法完整程序工程
OOOOO
OOO
O