Android中矩阵Matrix实现平移，旋转，缩放和翻转的用法详细介绍-编程知识

一，矩阵Matrix的数学原理

矩阵的数学原理涉及到矩阵的运算和变换，是高等代数学中的重要概念。在图形变换中，矩阵起到关键作用，通过矩阵的变换可以改变图形的位置、形状和大小。矩阵的运算是数值分析领域的重要问题，对矩阵进行分解和简化可以简化计算过程。对于一些特殊矩阵，如稀疏矩阵和准对角矩阵，有特定的快速运算算法。

在Matrix Matrix中，矩阵的数学原理同样适用。Matrix提供了缩放、平移、旋转和错切等操作，这些操作对应于特定的矩阵变换。例如，缩放操作对应于矩阵的元素乘以一个标量，平移操作对应于矩阵的元素加上一个偏移量，旋转操作则通过矩阵的置换和缩放来实现。

Matrix的数学原理在实际应用中非常重要。在图形处理、计算机视觉、机器学习等领域，都需要使用到矩阵运算和变换。掌握矩阵的数学原理有助于更好地理解和应用这些技术。

二，3x3矩阵的计算方法：

3x3矩阵的计算方法包括加法、减法、数乘和矩阵乘法。

加法是将两个3x3矩阵对应位置的元素相加，得到一个新的3x3矩阵。减法是将两个3x3矩阵对应位置的元素相减，得到一个新的3x3矩阵。数乘是将一个标量和一个3x3矩阵相乘，得到一个新的3x3矩阵。矩阵乘法是将两个3x3矩阵按照一定的规则相乘，得到一个新的3x3矩阵。

在进行矩阵乘法时，需要按照一定的规则进行计算，即左边矩阵的第一行的元素分别与右边矩阵的第一列的元素相乘，然后求和得到相乘矩阵的第一行的第一个元素。同样地，左边矩阵的第一行的元素分别与右边矩阵的第二列的元素相乘，求和得到相乘矩阵的第一行的第二个元素，以此类推。

另外，还有三阶矩阵乘法的公式：D=a11a22a33+a12a23a31+a13a21a32-a13a22a31-a12a21a33- a11a23a32。这个公式可以帮助我们快速地计算出两个3x3矩阵的乘积。

需要注意的是，在进行矩阵运算时，需要遵循一定的运算规则，如先进行括号内的运算，然后进行加、减、乘等运算，最后进行除法运算。同时，要注意矩阵的维数，即行数和列数，只有当两个矩阵的维数相同时才能进行矩阵运算。

三，四种变换的具体情形

1，平移变换
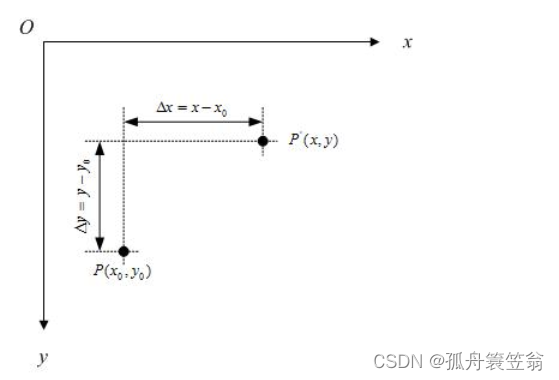
假定有一个点的坐标是 P_(x_0,y_0)将其移动到P_(x,y) ，再假定在x轴和y轴方向移动的大小分别为：
△x = x - x_0
△y = y - y_0
如下图所示：
在这里插入图片描述不难知道：
x = x_0 + △x
y = y_0 + △y
如果用矩阵来表示的话，就可以写成：

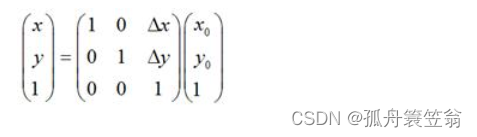
2，旋转变换
围绕坐标原点旋转

假定有一个点的坐标是 P_(x_0,y_0) ，相对坐标原点顺时针旋转 theta后的情形，同时假定P点离坐标原点的距离为r，如下图：
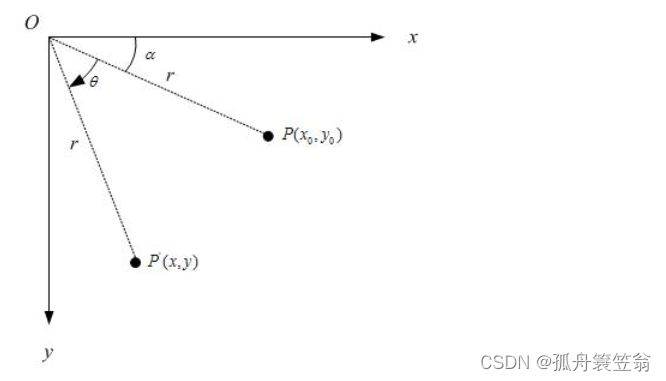在这里插入图片描述那么，
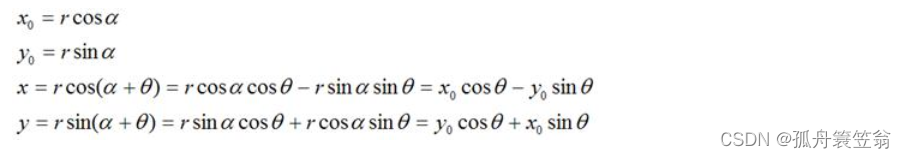如果用矩阵，就可以表示为：
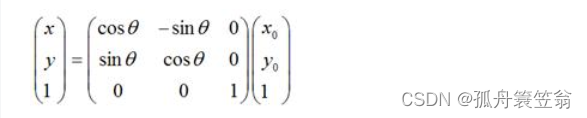3，缩放变换
理论上而言，一个点是不存在什么缩放变换的，但考虑到所有图像都是由点组成，因此，如果图像在x轴和y轴方向分别放大k1和k2倍的话，那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍，即：
x = k_1 x x_0
y = k_2 x y_0

用矩阵表示就是：
在这里插入图片描述 4，对称变换（翻转）
事实上，我们还可以利用Matrix，进行对称变换。所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如，某点经过对称变换后得到，
如果对称轴是x轴，那么，
x = x_0
y = -y_0
用矩阵表示就是：
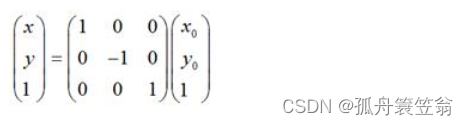
在这里插入图片描述
如果对称轴是y轴，那么，
x = -x_0
y =y_0

用矩阵表示就是：
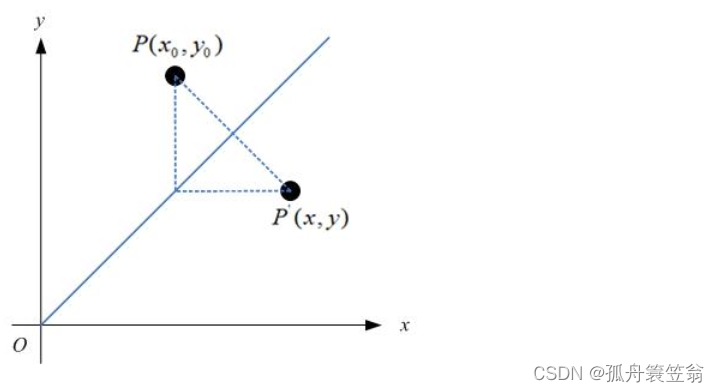
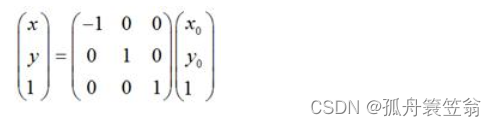在这里插入图片描述如果对称轴是y = x，如图：
四，基本方法解析

1，构造函数

public Matrix()
public Matrix(Matrix src)

构造函数有两个，第一个是直接创建一个单位矩阵，第二个是根据提供的矩阵创建一个新的矩阵（采用deep copy）

单位矩阵如下：
在这里插入图片描述 2，平移效果

public void setTranslate(float dx, float dy)

设置平移效果，参数分别是x，y上的平移量。
效果图如下：
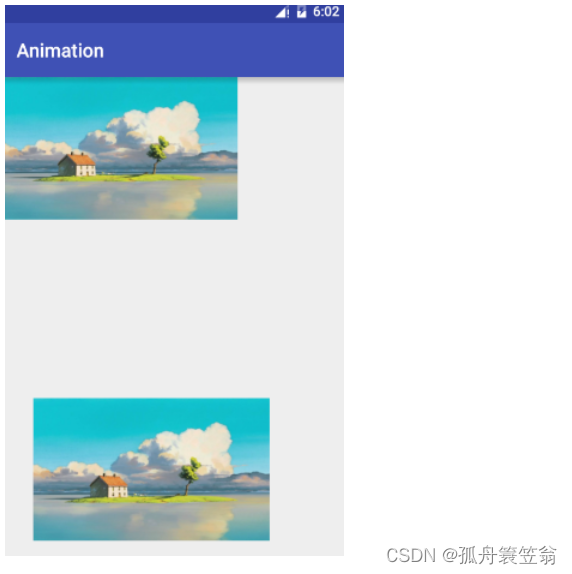
在这里插入图片描述
在Android中，Matrix 类用于执行各种2D图形变换，包括平移。以下是一个示例代码，展示如何使用 Matrix 实现平移：

Matrix matrix = new Matrix();  
matrix.setTranslate(dx, dy); // dx 和 dy 是平移的距离  // 假设你有一个 Bitmap 对象  
Bitmap bitmap = BitmapFactory.decodeResource(getResources(), R.drawable.my_image);  // 应用 Matrix 到 Bitmap 上  
Bitmap transformedBitmap = Bitmap.createBitmap(bitmap, 0, 0, bitmap.getWidth(), bitmap.getHeight(), matrix, true);  // 现在，transformedBitmap 是平移后的图像

在上述代码中，setTranslate 方法用于设置平移的距离。dx 和 dy 参数分别表示在x轴和y轴方向上的平移距离。然后，通过 createBitmap 方法将应用了平移变换的 Matrix 应用到一个 Bitmap 上，得到平移后的图像。

2，缩放效果

public void setScale(float sx, float sy, float px, float py)
public void setScale(float sx, float sy)

两个方法都是设置缩放到matrix中，sx，sy代表了缩放的倍数，px,py代表缩放的中心。这里跟上面比较类似不做讲解了。

3，旋转效果

public void setRotate(float degrees, float px, float py)
public void setRotate(float degrees)

看一个示例，我们把图像旋转90度，那么90度对应的sin和cos分别是1和0。
在这里插入图片描述
4，对称翻转
在Android中，Matrix类并没有直接提供实现对称的接口。对称变换通常涉及到更复杂的几何变换，包括旋转、平移和缩放等。Matrix类提供了一些基本的方法来实现这些变换，但如果你需要实现更复杂的对称变换，可能需要自定义实现或者使用其他图形处理库。

如果你需要实现对称变换，一种可能的解决方案是先对图像进行对称变换，然后再使用Matrix类的方法进行平移、旋转和缩放等操作。这需要一些几何知识来计算对称变换的矩阵，然后将其应用到图像上。

以下是一个示例代码，展示了如何使用Matrix类实现对称变换：

// 假设你有一个 Bitmap 对象  
Bitmap bitmap = BitmapFactory.decodeResource(getResources(), R.drawable.my_image);  // 定义对称变换的矩阵  
Matrix matrix = new Matrix();  
matrix.setScale(-1, 1); // 对称变换的矩阵  
matrix.postTranslate(bitmap.getWidth(), 0); // 执行对称变换后的平移  // 应用 Matrix 到 Bitmap 上  
Bitmap symmetricBitmap = Bitmap.createBitmap(bitmap, 0, 0, bitmap.getWidth(), bitmap.getHeight(), matrix, true);  // 现在，symmetricBitmap 是对称变换后的图像

在上述代码中，我们首先创建一个 Matrix 对象，并使用 setScale 方法设置对称变换的矩阵。这里我们使用了 -1 和 1 作为缩放因子，分别表示在x轴和y轴方向上的对称变换。然后，我们使用 postTranslate 方法将对称变换后的图像平移到正确的位置。最后，通过 createBitmap 方法将应用了对称变换和平移的 Matrix 应用到一个 Bitmap 上，得到对称变换后的图像。

需要注意的是，这只是一个简单的示例代码，实际的对称变换可能需要更复杂的矩阵计算。如果你需要实现更复杂的对称变换，可能需要使用更高级的图形处理库或者自定义实现。

五，高级方法解析

上面的基本方法中，有关于变换的set方法都可以带来不同的效果，但是每个set都会把上个效果清除掉，例如依次调用了setScale,setTranslate，那么最终只有setTranslate会起作用，那么如何才和将两种效果复合呢。Matrix给我们提供了很多方法。但是主要都是2类：

preXXXX：以pre开头，例如preTranslate
postXXXX：以post开头，例如postScale

他们分别代表了前乘，和后乘。看一段代码：

Matrix matrix = new Matrix();
matrix.setTranslate(100, 1000);
matrix.preScale(0.5f, 0.5f);

这里matrix前乘了一个scale矩阵，换算成数学式如下：
在这里插入图片描述
从上面可以看出，最终得出的matrix既包含了缩放信息也有平移信息。
后乘自然就是matrix在后面，而缩放矩阵在前面，由于矩阵前后乘并不等价，也就导致了他们的效果不同。我们来看看后乘的结果：
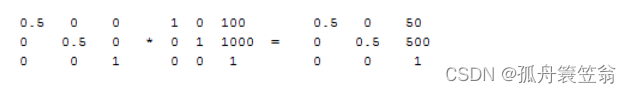可以看到，结果跟上面不同，并且这也不是我们想要的结果，这里缩放没有更改，但是平移被减半了，换句话说，平移的距离也被缩放了。所以需要注意前后乘法的关系。

matrix除了上面的方法外，还有一些其他的方法。

public boolean setRectToRect(RectF src, RectF dst, ScaleToFit stf)

在Android中，setRectToRect 是 Matrix 类的一个方法，用于将一个矩形（源矩形）转换到另一个矩形（目标矩形）。这个方法通常用于图形变换，例如在图像处理或绘图操作中。

该方法接受四个参数：

src：源矩形的左上角坐标（x, y）和其宽度和高度（width, height）。
dst：目标矩形的左上角坐标（x, y）和其宽度和高度（width, height）。
filterMin：缩放过滤模式的最小值。
filterMag：缩放过滤模式的最大值。

这个方法的作用是将源矩形转换为目标矩形，通过矩阵变换实现平移、缩放、旋转等操作。它可以根据需要选择不同的缩放过滤模式，以控制图像的平滑度和质量。

以下是一个示例代码，展示了如何使用 setRectToRect 方法进行图像变换：

Matrix matrix = new Matrix();  
// 设置源矩形的坐标和大小  
float srcLeft = 0;  
float srcTop = 0;  
float srcWidth = 100;  
float srcHeight = 100;  
// 设置目标矩形的坐标和大小  
float dstLeft = 50;  
float dstTop = 50;  
float dstWidth = 200;  
float dstHeight = 200;  
// 设置缩放过滤模式（使用线性插值）  
matrix.setRectToRect(new RectF(srcLeft, srcTop, srcLeft + srcWidth, srcTop + srcHeight),  new RectF(dstLeft, dstTop, dstLeft + dstWidth, dstTop + dstHeight),  Matrix.ScaleToFit.CENTER, Matrix.ScaleToFit.CENTER);  
// 应用矩阵到 Bitmap 上进行变换  
Bitmap transformedBitmap = Bitmap.createBitmap(bitmap, 0, 0, bitmap.getWidth(), bitmap.getHeight(), matrix, true);

在上述示例中，我们首先创建了一个 Matrix 对象，并使用 setRectToRect 方法将源矩形转换为目标矩形。这里，我们使用了线性插值作为缩放过滤模式，使图像在变换过程中保持平滑。然后，我们将应用了矩阵变换的 Matrix 应用到一个 Bitmap 上，得到变换后的图像。

ScaleToFit 有如下四个值：

FILL: 可能会变换矩形的长宽比，保证变换和目标矩阵长宽一致。
START:保持坐标变换前矩形的长宽比，并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。左上对齐。
CENTER: 保持坐标变换前矩形的长宽比，并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。
END:保持坐标变换前矩形的长宽比，并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。右下对齐。

你的鼓励将是我创作的最大动力，求大神打赏！！！
在这里插入图片描述