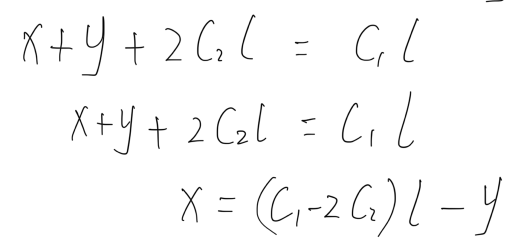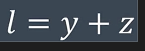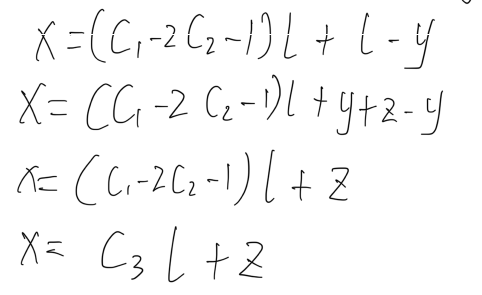本文灵感来自哔哩哔哩视频
视频链接:
弗洛伊德循环查找算法
算法代码(java)
package rain;class ListNode {int value;ListNode next;public ListNode(int value) {this.value = value;this.next = null;}@Overridepublic String toString() {return "ListNode{" +"value=" + value +'}';}
}
public class FloydCycleDetectionAlgrithm {public static void main(String[] args) {ListNode node0 = new ListNode(4);ListNode node1 = new ListNode(3);ListNode node2 = new ListNode(7);ListNode node3 = new ListNode(8);ListNode node4 = new ListNode(6);ListNode node5 = new ListNode(9);ListNode node6 = new ListNode(2);ListNode node7 = new ListNode(1);ListNode node8 = new ListNode(5);ListNode node9 = new ListNode(2);node0.next = node4;node1.next = node3;node2.next = node7;node3.next = node8;node4.next = node6;node5.next = node9;node6.next = node2;node7.next = node1;node8.next = node5;node9.next = node2;ListNode node = Find(node0);System.out.println(node);}public static ListNode Find(ListNode head) {ListNode slow = head;ListNode fast = head;while (true) {slow = slow.next;fast = fast.next.next;//第一次相遇//if slow and fast meet, then break the loopif (fast == slow) {break;}}//第二次相遇slow = head;while (true) {slow = slow.next;fast = fast.next;if (fast == slow) {return fast;}}}
}
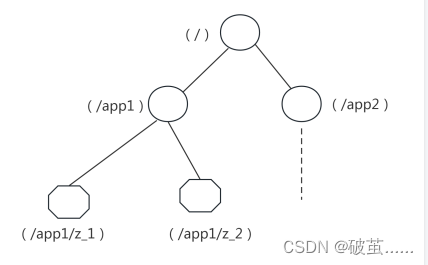
弗洛伊德循环查找算法中第二次相遇的地方就是循环的起始点,这个性质的证明是基于数学的原理。这是因为在第一次相遇时,慢指针 `slow` 和快指针 `fast` 已经处于同一个循环内。设链表起点到环的起始点的距离为 X,环的起始点到第一次相遇点的距离为 Y,第一次相遇点到环的起始点的距离为Z。
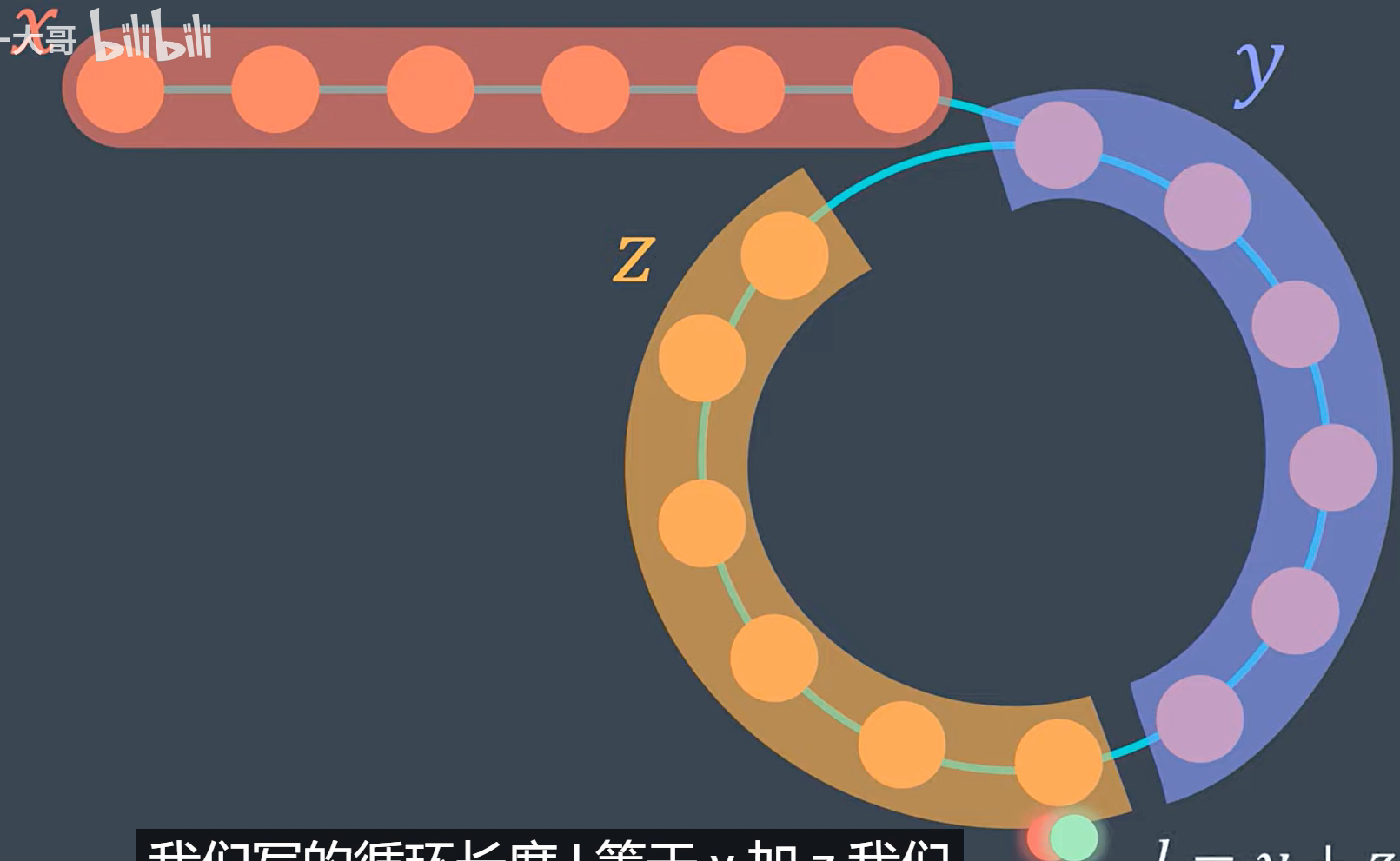
第一次相遇
ListNode slow = head;ListNode fast = head;while (true) {slow = slow.next;fast = fast.next.next;//第一次相遇//if slow and fast meet, then break the loopif (fast == slow) {break;}}设循环长度
1. 在第一次相遇时,慢指针 `slow` 走的距离,
C2是常数
而快指针 `fast` 走 的距离
2. 由于快指针的速度是慢指针的两倍,所以快指针走的距离是慢指针的两倍。因此,有
3. 进一步简化上述等式,得到
这意味着
循环前的距离X = 一定数量循环次数 减去 汇合点前距离Y
4.因为
可得
C3乘以 循环长度长度l 意味着固定的循环量!
找到节点只需要让两个节点分别走X和C3l+Z的路程
此时, 我们可以把slow放在起始位置 每次走一格,
同时 让fast也是每次走一格
直到相遇 fast == slow 说明相遇的节点就是循环开始的节点
//第二次相遇slow = head;while (true) {slow = slow.next;fast = fast.next;if (fast == slow) {return fast;}}也就是说,如果此时将慢指针重新指向链表起始点,慢指针再次移动 X 的距离,而快指针从第一次相遇点开始移动 C3l+Z 的距离,它们将会在环的起始点再次相遇。
因此,第二次相遇的地方就是循环的起始点。这个性质是弗洛伊德循环查找算法的关键之一,也是该算法能够正确找到环的起始点的原因。
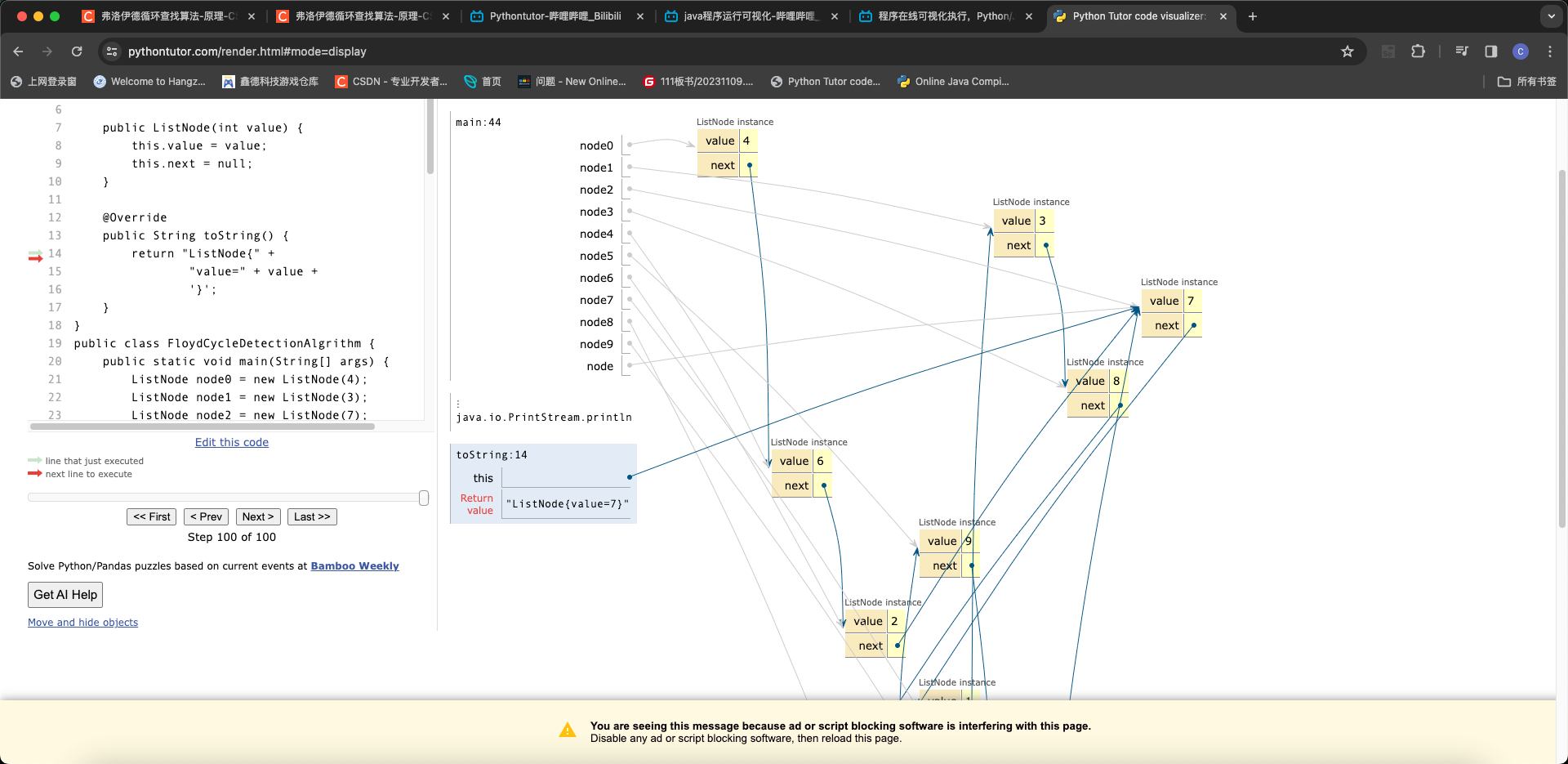
文末推荐我常用的一个学习网站 可视化运行程序
比如这段链表就可以直观展示出来
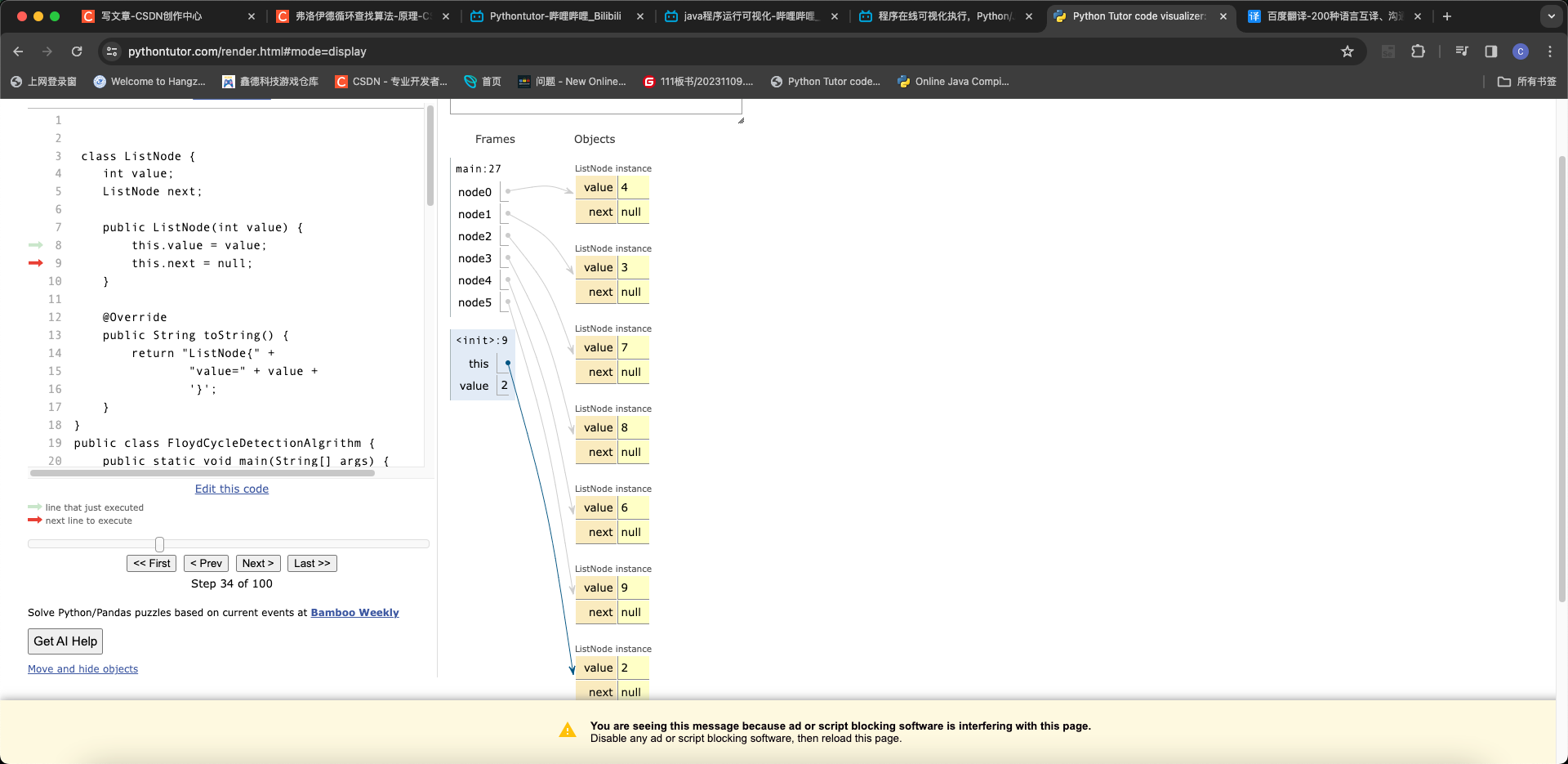
网站链接
可视化运行网站