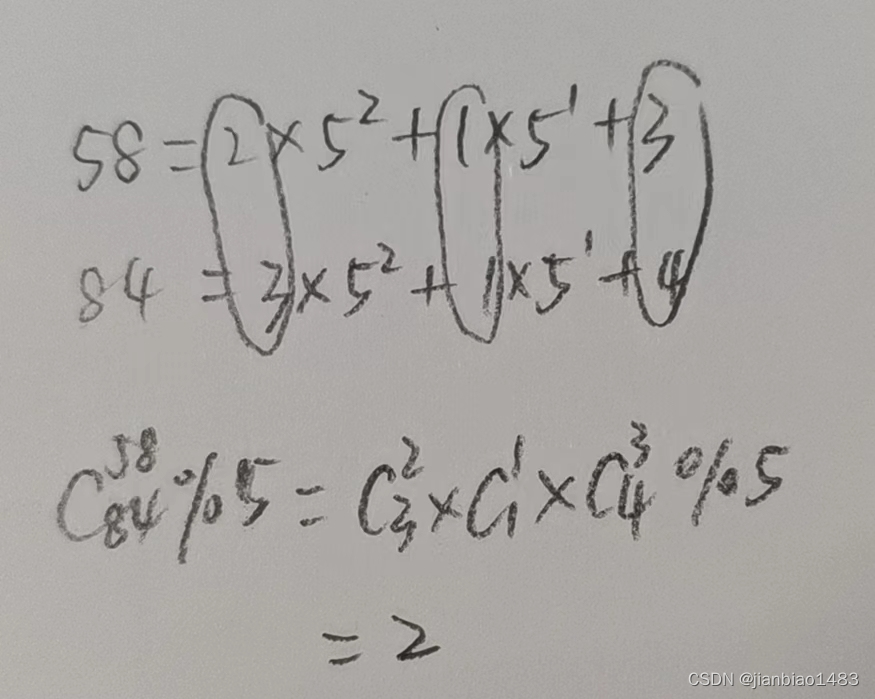将大组合数C（n,m）%p分解为小组合数C（n,m）%p乘积的模，n<=10^18,m<=10^18。

其中求解小组合数可以根据定义式计算（质因子分解），也可以通过定义式的变形计算（逆元）

一、定义式计算（质因子分解-快速幂）

快速幂计算每一组pi^ci%p，然后相乘取模

#include<stdio.h>
//素数表(筛法)
const int maxn=1000000;
int prime[maxn];
int pNum=0;
bool p[maxn]={false};
void Find_Prime(){for(int i=2;i<maxn;i++){if(p[i]==false){prime[pNum++]=i;for(int j=i+i;j<maxn;j+=i){p[j]=true;}}} 
}//n!中含质因子p个数
int cal(int n,int p){int ans=0;while(n){ans+=n/p;n/=p;}return ans;
}//快速幂求a^b%p 
typedef long long LL; 
LL binaryPow(LL a,LL b,LL m){if(b==0) return 1;if(b&1) return a*binaryPow(a,b-1,m)%m;else{LL mul=binaryPow(a,b/2,m);return mul*mul%m;}
}//小组合数C(n,m)%p 
//遍历素数表中每一个质因子，计算每一组pi^ci%p，然后相乘取模
int C(int n,int m,int p){int ans=1;for(int i=0;prime[i]<=n;i++){int c=cal(n,prime[i])-cal(m,prime[i])-cal(n-m,prime[i]); //C(n,m)中含质因子个数 ans=ans*binaryPow(prime[i],c,p)%p;}return ans;
} //Lucas定理求大组合数C(n,m)%p
int  Lucas(int n,int m,int p){if(m==0) return 1;return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;
} int main(){Find_Prime();int n,m,p;scanf("%d%d%d",&n,&m,&p);printf("%d",Lucas(n,m,p));return 0;
}

二、定义式的变形计算（逆元）

#include<stdio.h>
//扩展欧几里得（解出x） 
int exGcd(int a,int m,int &x,int &y){if(m==0){x=1;y=0;return a;}int g=exGcd(m,a%m,x,y);int temp=x;x=y;y=temp-(a/m)*y;return g;
}//逆元（得0-m范围内的解）
int inverse(int a,int m){int x,y;int g=exGcd(a,m,x,y);return (x%m+m)%m;
}//求小组合数C(n,m)%p 
int C(int n,int m,int p){int ans=1;for(int i=1;i<=m;i++){ans=ans*(n-m+i)%p;ans=ans*inverse(i,p)%p;}return ans; 
}//Lucas求大组合数 C(n,m)%pint Lucas(int n,int m,int p){if(m==0) return 1;return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;}int main(){int n,m,p;scanf("%d%d%d",&n,&m,&p);printf("%d",Lucas(n,m,p));return 0;}

运行结果：

C（84,58）%5=2