数据结构实验6：图的应用

目录

一、实验目的

1. 邻接矩阵

2. 邻接矩阵表示图的结构定义

 3. 图的初始化

4. 边的添加

 5. 边的删除

6. Dijkstra算法 

三、实验内容

实验内容

代码

截图

分析

一、实验目的

1．掌握图的邻接矩阵的存储定义；

2．掌握图的最短路径（Dijsktra）算法的实现。

二、实验原理

1. 邻接矩阵

邻接矩阵是一种表示图的方法。它是一个二维数组，用于表示图中各个顶点之间的连接关系。如果图是有向图，那么邻接矩阵是对称的；如果是无向图，邻接矩阵可能不是对称的。

  1. 顶点的编号： 假设图有n个顶点，通常是从1到n。

  2. 构建矩阵： 创建一个n x n的矩阵，其中元素a[i][j]表示顶点i到顶点j是否有边。如果存在边，通常用1表示；如果不存在边，通常用0表示。

    例如，对于无向图，如果顶点i和顶点j之间有边，则a[i][j]和a[j][i]都设置为1。对于有向图，只需设置a[i][j]为1表示从顶点i到顶点j有一条有向边。

  3. 权重： 如果图中的边有权重，可以在矩阵中存储这些权重。矩阵的元素a[i][j]可以表示从顶点i到顶点j的权重值。

2. 邻接矩阵表示图的结构定义

#define MAX_SIZE 100struct Graph {int numVertices;//节点数int adjMatrix[MAX_SIZE][MAX_SIZE];//邻接矩阵
};

 3. 图的初始化

创建一个空的图数据结构并为其设置初始状态。

void InitializeGraph(struct Graph* graph,int num) {int i, j;graph->numVertices = num;for (i = 0; i < num; i++) {for (j = 0; j < num; j++) {graph->adjMatrix[i][j] = 0;}}
}

4. 边的添加

 在图中增加边，将该边置为1，表示存在，或者权值

若是无向图，由于对称性，则需要改变两条边

//添加边
void addEdge(struct Graph* graph, int startVertex, int endVertex) {graph->adjMatrix[startVertex][endVertex] = 1;//若是无向图graph->adjMatrix[endVertex][startVertex] = 1;
}

 5. 边的删除

置为0(不存在)或者无限大的权值

void deleteEdge(struct Graph* graph, int startVertex, int endVertex) {graph->adjMatrix[startVertex][endVertex] = 0;//若是无向图graph->adjMatrix[endVertex][startVertex] = 0;
}

6. Dijkstra算法 

Dijkstra算法是一种用于在带有非负权重的图中找到单源最短路径的算法。该算法的基本思想是从起始顶点开始，逐步扩展到离起始顶点的距离最短的顶点，直到到达目标顶点为止。

  1. 初始化： 对于每个顶点v，初始化距离值dist[v]为无穷大（表示尚未到达该顶点），并将起始顶点的距离值dist[start]设置为0。创建一个优先队列（最小堆），将起始顶点加入队列。

  2. 更新距离值： 从优先队列中取出距离值最小的顶点u。对于u的每个邻接顶点v，如果通过u可以缩短到达v的距离（dist[start] + weight(u, v) < dist[v]），则更新dist[v]的值。更新后，将v加入优先队列。

  3. 重复步骤2： 重复上述步骤，直到优先队列为空。这样，对于每个顶点，dist数组中存储的值就是从起始顶点到达该顶点的最短路径距离。

Dijkstra算法的关键在于通过贪心策略，每次选择距离起始顶点最近的顶点进行扩展。这确保了每个顶点的最短路径被逐步确定，直到到达目标顶点

//Dijkstra算法
void dijkstra(struct Graph* graph, int startVertex) {int dist[MAX_SIZE];  // 存储从起始节点到各节点的最短距离int visited[MAX_SIZE] = { 0 };  // 标记节点是否被访问过// 初始化距离数组for (int i = 0; i < graph->numVertices; i++) {dist[i] = INT_MAX;}// 起始节点到自身的距离为0dist[startVertex] = 0;for (int count = 0; count < graph->numVertices - 1; count++) {int minDist = 9999;int minIndex;// 选择距离最小的未访问节点for (int v = 0; v < graph->numVertices; v++) {if (!visited[v] && dist[v] < minDist) {minDist = dist[v];//当前最短距离minIndex = v;//当前最短的点}}// 标记节点为已访问visited[minIndex] = 1;// 更新最短距离数组//!visited[v]：检查节点 v 是否已经被访问过，如果节点已经被访问过，则不需要更新最短距离。//graph->adjacencyMatrix[minIndex][v] != 9999：检查从当前节点 minIndex 到节点 v 是否存在边。9999 表示两个节点之间没有直接的连接，因此如果这个条件为真，说明节点 minIndex 和节点 v 之间存在边。// dist[minIndex] != 9999：检查起始节点到节点 minIndex 的最短距离是否已经被初始化，如果没有被初始化，说明当前节点 minIndex 不可达，无法通过它来更新其他节点的距离。//(dist[minIndex] + graph->adjMatrix[minIndex][v] < dist[v])：检查通过当前节点 minIndex 更新节点 v 的距离是否比已知的最短距离 dist[v] 更短。如果是，就更新 dist[v] 为更短的距离。for (int v = 0; v < graph->numVertices; v++) {if (!visited[v] && graph->adjMatrix[minIndex][v] != 9999 && dist[minIndex] != 9999 && (dist[minIndex] + graph->adjMatrix[minIndex][v] < dist[v])) {dist[v] = dist[minIndex] + graph->adjMatrix[minIndex][v];}}}// 打印最短距离cout<<"从"<< startVertex<<"节点为起点"<<endl;for (int i = 0; i < graph->numVertices; i++) {cout<<"到"<<i<<"节点的最短距离为：" << dist[i]<<endl;}
}

三、实验内容

实验内容

必做内容：

设计安徽大学的校园平面图，所含景点不少于 8 个。以图中顶点表示学校内各景点，存放景点的名称、景点介绍信息等；以边表示路径，存放路径长度信息。要求将这些信息保存在文件 graph.txt 中，系统执行时所处理的数据要对此文件分别进行读写操作。

1．从文件 graph.txt 中读取相应数据, 创建一个图,使用邻接矩阵表示图；

2．景点信息查询：为来访客人提供校园任意景点相关信息的介绍；

3．问路查询：为来访客人提供校园任意两个景点之间的一条最短路径；

选做内容（对文件进行操作，相应信息变化后，再次进行景点信息查询和

问路查询时应该有所体现）：

1. 修改一个已有景点的相关信息；

2. 增加一个新景点及其相关信息；

3. 增加一条新的路径；

4. 删除一个景点及其相关信息；

5. 删除一条路径。

代码

#define _CRT_SECURE_NO_WARNINGS
#include<fstream>
#include<iostream>
using namespace std;#define MAX_SIZE 100struct Graph {int numVertices;//节点数int adjMatrix[MAX_SIZE][MAX_SIZE];//邻接矩阵，用来储存距离char address[MAX_SIZE][MAX_SIZE];//景点名称char intro[MAX_SIZE][MAX_SIZE];//景点介绍
};//图的初始化
void InitializeGraph(struct Graph* graph,int num) {int i, j;graph->numVertices = num;for (i = 0; i < num; i++) {for (j = 0; j < num; j++) {graph->adjMatrix[i][j] = 9999;}}
}//添加边
void addEdge(struct Graph* graph, int startVertex, int endVertex,int length) {graph->adjMatrix[startVertex][endVertex] = length;//若是无向图graph->adjMatrix[endVertex][startVertex] = length;
}//删除边
void deleteEdge(struct Graph* graph, int startVertex, int endVertex) {graph->adjMatrix[startVertex][endVertex] = 0;//若是无向图graph->adjMatrix[endVertex][startVertex] = 0;
}//找到编号对应的景点名称
void find_address(struct Graph* graph, int index) {cout << graph->address[index];
}//Dijkstra算法
void dijkstra(struct Graph* graph, int startVertex, int endVertex) {int visited[MAX_SIZE] = { 0 };//记录是否被访问过int pre[MAX_SIZE] = { startVertex };//记录前驱点编号int min_leng[MAX_SIZE];for (int i = 0; i < MAX_SIZE; i++) {min_leng[i] = 9999;}visited[startVertex] = 1;int min_length = 9999;int min_index = startVertex;//第一轮for (int j = 0; j < graph->numVertices; j++) {if (visited[j] == 0) {//如果未被访问过//cout << graph->adjMatrix[startVertex][j] << "   " << min_leng[j] << endl;if (graph->adjMatrix[startVertex][j]  < min_leng[j]) {//如果新的起始点到达终点的距离更短，则前驱节点为新的起始点//find_address(graph, j);pre[j] = startVertex;min_leng[j] = graph->adjMatrix[startVertex][j] ;}}//cout << endl;for (int j = 0; j < graph->numVertices; j++) {//找最短路径作为新一轮的起始点if (visited[j] == 0) {//如果未被访问过if (min_leng[j] < min_length) {min_length = min_leng[j];min_index = j;}}}visited[min_index] = 1;}for (int i = 0; i < graph->numVertices - 2; i++) {//共顶点数-2轮    for (int j = 0; j < graph->numVertices; j++) {if (visited[j] == 0) {//如果未被访问过//cout <<graph-> adjMatrix[min_index][j]<<"   " << min_leng[j] << endl;if ((graph->adjMatrix[min_index][j] + min_length) < min_leng[j]) {//如果新的起始点到达终点的距离更短，则前驱节点为新的起始点//find_address(graph, j);pre[j] = min_index;min_leng[j] = graph->adjMatrix[min_index][j] + min_length;}}//cout << endl;}//cout << "更新一轮"<<endl;for (int j = 0; j < graph->numVertices; j++) {//cout << min_leng[j] << " ";}min_length = 9999;min_index = startVertex;for (int j = 0; j < graph->numVertices; j++) {//找最短路径作为新一轮的起始点if (visited[j] == 0) {//如果未被访问过if (min_leng[j] < min_length) {min_length = min_leng[j];min_index = j;}}}visited[min_index] = 1;//cout << "这一轮起始点为";//find_address(graph, min_index);// cout << endl << "到达起始点距离为" << min_length << endl;}cout <<"最短距离为："<< min_leng[endVertex]<<endl;//输出最短路径，从后往前找前驱cout << "最短路径为：";int count = 2;int road[MAX_SIZE] ;for (int i = 0; i < MAX_SIZE; i++) {road[i] = endVertex;}road[0] = startVertex;int end = endVertex;//尾while (pre[end] != startVertex) {//计算路径中的景点数count++;end = pre[end];}end = endVertex;for (int i = count - 2; i >= 0; i--) {road[i] = pre[end];end = pre[end];}int flag = 1;for (int i = 0; i < count; i++) {if (flag == 0) {cout << "->";}find_address(graph, road[i]);flag = 0;}return;
}//找到该景点对应的编号
int find_index(struct Graph* graph, char string[]) {for (int i = 0; i < graph->numVertices; i++) {if (strcmp(string, graph->address[i]) == 0) {return i;}}cout << "不存在该景点" << endl;return -1;
}//景点信息查询
void volun1(struct Graph* graph) {cout << "本校景点有：" << endl;for (int i = 0; i < graph->numVertices; i++) {cout <<i<<":"<< graph->address[i] << endl;}char string1[MAX_SIZE];cout << "请输入你要查询的景点:";cin >> string1;int index = find_index(graph, string1);cout << graph->intro[index] << endl;
}//最短路径查询
void volun2(struct Graph* graph) {char source[MAX_SIZE], destination[MAX_SIZE];cout << "请输入起始景点和目的景点:";cin >> source >> destination;int start = 0, end = 0;start = find_index(graph, source);end = find_index(graph, destination);dijkstra(graph, start, end);cout << endl;
}//增加景点相关信息
void volun3(struct Graph* graph) {char address[MAX_SIZE], intro[MAX_SIZE];cout << "请输入你要增加的景点名称及其相关信息："<<endl;cin >> address >> intro;//将信息复制进去strcpy(graph->address[graph->numVertices], address);strcpy(graph->intro[graph->numVertices], intro);graph->numVertices++;//修改节点数//相关路径全改为无穷大for (int i = 0; i < graph->numVertices; i++) {graph->adjMatrix[i][graph->numVertices - 1] = 9999;}for (int i = 0; i < graph->numVertices; i++) {graph->adjMatrix[graph->numVertices - 1][i] = 9999;}
}//修改景点的相关信息
void volun4(struct Graph* graph) {char address[MAX_SIZE], intro[MAX_SIZE];cout << "请输入你要修改的景点名称及其相关信息：" << endl;cin >> address >> intro;//找到编号int des_index = find_index(graph, address);//修改memset(graph->intro[des_index], MAX_SIZE, sizeof(char));//清空strcpy(graph->intro[des_index], intro);
}//增加路径
void volun5(struct Graph* graph) {char source[MAX_SIZE], destination[MAX_SIZE]; int length;cout << "请输入你要增加的路径:" << endl;cin >> source >> destination >> length;int start = find_index(graph, source);int end = find_index(graph, destination);addEdge(graph, start, end, length);
}//删除一个景点及其相关信息
void volun6(struct Graph* graph) {char address[MAX_SIZE];cout << "请输入你要删除的景点：" << endl;cin >> address;int index = find_index(graph, address);//清空memset(graph->address[index], MAX_SIZE, sizeof(char));memset(graph->intro[index], MAX_SIZE, sizeof(char));
}//删除一条路径
void volun7(struct Graph* graph) {char source[MAX_SIZE], destination[MAX_SIZE];cout << "请输入你要删除的路径:" << endl;cin >> source >> destination;int start = find_index(graph, source);int end = find_index(graph, destination);deleteEdge(graph, start, end);
}int main() {struct Graph q;int num_V, num_a;//顶点数目，边的个数FILE* filePointer;filePointer = fopen("C:\\Users\\Administrator\\Desktop\\graph.txt", "r");// 检查文件是否成功打开if (filePointer == NULL) {cout << "无法打开文件";return 1; // 退出程序}char buffer[1000];char Address[MAX_SIZE], Intro[MAX_SIZE];// 读取一行数据if (fgets(buffer, sizeof(buffer), filePointer) != NULL) {if (sscanf(buffer, "%d %d", &num_V, &num_a) == 2) {q.numVertices = num_V;//cout << num_V << " " << num_a<<endl;}else {cout<<"错误：无法从字符串中提取两个数字。" << endl;}} else {cout<<"错误：文件为空或无法读取。" << endl;}InitializeGraph(&q, num_V);//初始化图//读取景点名称及其介绍for (int i = 0; i < num_V; i++) {if (fgets(buffer, sizeof(buffer), filePointer) != NULL) {if (sscanf(buffer, "%s %s", Address, Intro) == 2) {strcpy(q.address[i], Address);strcpy(q.intro[i], Intro);//cout << q.address[i] << endl;//cout << q.intro[i] << endl;}else {printf("错误：无法从字符串中提取两个字符串。\n");}}else {cout << "错误：文件为空或无法读取。" << endl;}}//读取景点之间距离char source[MAX_SIZE], destination[MAX_SIZE];int length=0;for (int i = 0; i < num_a; i++) {if (fgets(buffer, sizeof(buffer), filePointer) != NULL) {if (sscanf(buffer, "%s %s %d", source, destination,&length) == 3) {int index1 = find_index(&q, source);int index2 = find_index(&q, destination);q.adjMatrix[index1][index2] = length;q.adjMatrix[index2][index1] = length;//cout << index1 << " " << index2 << " " << length << endl;}else {cout<<"错误：无法从字符串中提取两个字符串，一个数字。"<<endl;}}else {cout << "错误：文件为空或无法读取。" << endl;}}// 关闭文件fclose(filePointer);//信息填充完毕，接下来是查阅环节int code;cout << "********************欢迎来到安徽大学！********************" << endl;cout << "               1.查询景点信息" << endl;cout << "               2.问路查询" << endl;cout << "               3.增加一个景点及其相关信息" << endl;cout << "               4.修改一个景点的相关信息" << endl;cout << "               5.增加一个新的路径" << endl;cout << "               6.删除一个景点及其相关信息" << endl;cout << "               7.删除一条路径" << endl;cout << "               8.退出" << endl;cout << "********************安大校园导游系统*********************" << endl;cout << "请选择需要的服务：(1-8)" << endl;cin >> code;while (code != 8) {switch (code){case 1: volun1(&q);          break;case 2: volun2(&q);          break;case 3: volun3(&q);          break;case 4: volun4(&q);          break;case 5: volun5(&q);          break;case 6: volun6(&q);          break;case 7: volun7(&q);          break;}cin >> code;}cout << "退出" << endl;return 0;
}

截图

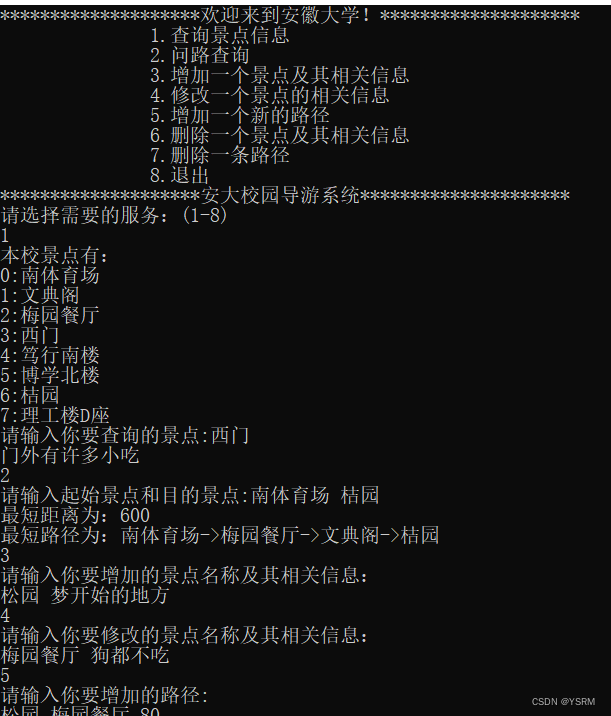
分析

对于上述代码，是存在一个问题的，比如增加一个节点，删除俩个节点，总数目减少，但是最大索引值是在增加的，所以再次实现其他功能的时候是不切实际的

way1：提供一个有效位数组，按最大索引值的范围查找

way2: 当删除时，后面的节点索引值应该加以改变，但是很麻烦

此外上述代码提到了sscanf函数

sscanf函数接受一个字符串作为输入，并根据指定的格式从该字符串中读取数据，然后将数据存储在相应的变量中。

#include <stdio.h>int sscanf(const char *str, const char *format, ...);
  • str是包含格式化数据的输入字符串。
  • format是描述输入字符串中数据格式的格式字符串。
  • 可变参数（...）是用于存储从输入字符串中读取的数据的变量列表。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/414192.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

网络安全产品之认识WEB应用防火墙

网络安全产品之认识WEB应用防火墙

随着B/S架构的广泛应用&#xff0c;Web应用的功能越来越丰富&#xff0c;蕴含着越来越有价值的信息&#xff0c;应用程序漏洞被恶意利用的可能性越来越大&#xff0c;因此成为了黑客主要的攻击目标。传统防火墙无法解析HTTP应用层的细节&#xff0c;对规则的过滤过于死板&#…
阅读更多...
VsCode重新安装需要配机的ESLint和 Prettier - Code formatter 配置

VsCode重新安装需要配机的ESLint和 Prettier - Code formatter 配置

新电脑安装完Vscode后&#xff0c;需要装几个插件&#xff0c;这里记录下&#xff1a; {"diffEditor.ignoreTrimWhitespace": false,"files.autoSave": "afterDelay","editor.codeActionsOnSave": {"source.fixAll.eslint"…
阅读更多...
【leetcode】消失的数字

【leetcode】消失的数字

大家好&#xff0c;我是苏貝&#xff0c;本篇博客带大家刷题&#xff0c;如果你觉得我写的还不错的话&#xff0c;可以给我一个赞&#x1f44d;吗&#xff0c;感谢❤️ 目录 1.暴力求解法2.采用异或的方法&#xff08;同单身狗问题&#xff09;3.先求和再减去数组元素 点击查看…
阅读更多...
Leetcode刷题笔记题解（C++）：200. 岛屿数量

Leetcode刷题笔记题解（C++）：200. 岛屿数量

思路&#xff1a;利用深度优先搜索的思路来查找1身边的1&#xff0c;并且遍历之后进行0替换防止重复dfs&#xff0c;代码如下所示 class Solution { public:int numIslands(vector<vector<char>>& grid) {int row grid.size();int col grid[0].size();int n…
阅读更多...
Unity之四元数

Unity之四元数

欧拉角 万向节死锁 四元数是什么 Unity中四元数的初始化 四元数和欧拉角的互相转换 补充 四元数相乘代表旋转四元数
阅读更多...
一张图描述Http常用状态码（301、302、305、404、408等等）

一张图描述Http常用状态码（301、302、305、404、408等等）

301—永久移动。被请求的资源已被永久移动位置&#xff1b; 302—请求的资源现在临时从不同的 URI 响应请求&#xff1b; 305—使用代理。被请求的资源必须通过指定的代理才能被访问&#xff1b; 307—临时跳转。被请求的资源在临时从不同的URL响应请求&#xff1b; 40…
阅读更多...
往docker中cloudbeaver的容器添加达梦数据库、impala数据库连接支持（cloudbeaver添加自定义数据连接）

往docker中cloudbeaver的容器添加达梦数据库、impala数据库连接支持（cloudbeaver添加自定义数据连接）

cloudbeaver默认没有开放impala连接&#xff0c;更不会支持国产数据库了 docker安装运行cloudbeaver可以参考文章&#xff1a;docker安装运行CloudBeaver并设置默认语言为中文 本文跳过cloudbeaver镜像拉取&#xff0c;直接就开始实现自定义数据库连接功能 1、初始化cloudbe…
阅读更多...
浅谈：完成一篇论文的科研历程与经验

浅谈：完成一篇论文的科研历程与经验

作者&#xff1a;彭思达 | CCF专业会员 浙江大学研究员 主要研究方向为三维计算机视觉 | 本文版权归作者所有 文章目录 引言阶段1&#xff1a;想idea阶段2&#xff1a;如何做实验阶段3&#xff1a;如何写论文 引言 完成一篇论文的常见科研历程包括三大阶段&#xff1a;想idea、…
阅读更多...
go语言（七）----slice的声明方式

go语言（七）----slice的声明方式

1、声明方式一 //声明一个slice1是一个切片&#xff0c;但是并没有给slice分配空间var slice1 []intslice1 make([]int,3)2、声明方式二 声明一个slice切片&#xff0c;同时给slice分配空间&#xff0c;3个空间&#xff0c;初始化值是0var slice1 []int make([]int,3)3、声…
阅读更多...
scipy测试数据

scipy测试数据

文章目录 图像心电图 图像 scipy的datasets中提供了几组在图像和信号处理中可能会用到的数据&#xff0c;但是&#xff0c;如果想顺利使用&#xff0c;还需要安装一个scipy的依赖模块pooch pip install pooch然后就可以加载这几种数据了 from scipy.datasets import ascent,…
阅读更多...
最多购买宝石数目 - 华为OD统一考试

最多购买宝石数目 - 华为OD统一考试

OD统一考试&#xff08;C卷&#xff09; 分值&#xff1a; 100分 题解&#xff1a; Java / Python / C 题目描述 橱窗里有一排宝石&#xff0c;不同的宝石对应不同的价格&#xff0c;宝石的价格标记为 gems[i],0<i<n, n gems.length 宝石可同时出售0个或多个&#xff…
阅读更多...
百度搜索Push个性化：新的突破

百度搜索Push个性化：新的突破

作者 | 通用搜索产品研发组 导读 本文简单介绍了百度搜索Push个性化的发展过程&#xff0c;揭示了面临的困境和挑战&#xff1a;如何筛选优质物料、如何对用户精准推荐等。我们实施了一系列策略方法进行突破&#xff0c;提出核心的解决思路和切实可行的落地方案。提升了搜索DAU…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023