【信号与系统】【北京航空航天大学】实验四、幅频、相频响应和傅里叶变换

一、实验目的

1、 掌握利用MATLAB计算系统幅频、相频响应的方法；
2、 掌握使用MATLAB进行傅里叶变换的方法；
3、 掌握使用MATLAB验证傅里叶变换的性质的方法。

二、实验内容

1、
在这里插入图片描述
MATLAB代码：

>> clear all;
>> a = [1 3 2];
>> b = [1];
>> w = -2 * pi : 0.01 : 2 * pi;
>> [H, w] = freqs(b, a, w);
>> mag = abs(H);
>> pha = angle(H);
>> rea = real(H);
>> ima = imag(H);
>> figure
>> subplot(2, 1, 1);
>> plot(w, mag);
>> grid on;
>> xlabel('\omega/\omega_0');
>> ylabel('|H(jw)|');
>> title('幅频响应曲线');
>> axis([-2 * pi, 2 * pi, 0, 0.6]);
>> subplot(2, 1, 2);
>> plot(w, pha);
>> grid on;
>> xlabel('\omega/\omega_0');
>> ylabel('∠H(jw) (rad)');
>> title('相频响应曲线');
>> axis([-2 * pi, 2 * pi, 0, 0.6]);
>> axis([-2 * pi, 2 * pi, -3, 3]);
>> figure
>> subplot(2, 1, 1);
>> plot(w, rea);
>> axis([-2 * pi 2 * pi -0.1 0.6]);
>> grid on;
>> xlabel('\omega/\omega_0');
>> ylabel('Re{H(jw)}');
>> title('频率响应的实部');
>> subplot(2, 1, 2);
>> plot(w, ima);
>> xlabel('\omega/\omega_0');
>> ylabel('Im{H(jw)}');
>> axis([-2 * pi 2 * pi -0.4 0.4]);
>> grid on;
>> title('频率响应的虚部');

幅频响应、相频响应曲线：

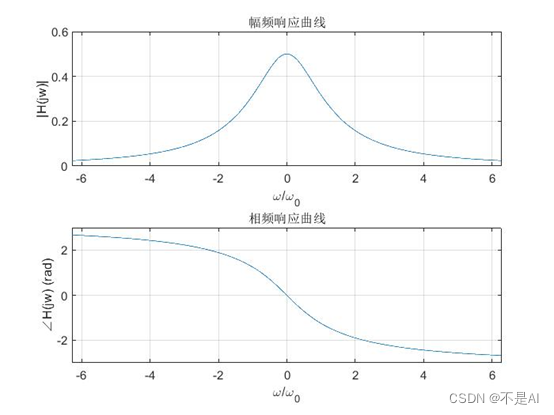
在这里插入图片描述

频率响应的实部和虚部：

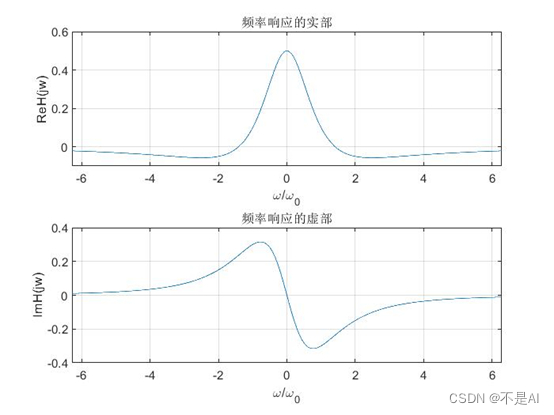
在这里插入图片描述

2、

在这里插入图片描述

MATLAB代码：

（1）X1(t) 信号

>> clear all;
>> syms x;
>> f = exp(-x) .* heaviside(x);
>> F = fourier(f);
>> Fs = abs(F);
>> Fe = angle(F);
>> figure
>> subplot(2, 1, 1);
>> ezplot(Fs, [-2 * pi, 2 * pi]);
>> title('符号计算X1(jw)的幅度谱', 'FontSize', 14);
>> grid on;
>> xlabel('\omega/\omega_0');
>> ylabel('|X1(jw)|');
>> subplot(2, 1, 2);
>> ezplot(Fe, [-2 * pi, 2 * pi]);
>> title('符号计算X1(jw)的相位谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('∠X1(jw) (rad)');
>> grid on;
>> clear all;
>> T = 0.01;
>> dw = 0.01;
>> t = -5 : T : 5;
>> w = -2 * pi : dw : 2 * pi;
>> f = exp(-t) .* (t >= 0);
>> F = f * exp(-j * t' * w) * T;
>> Fe = angle(F);
>> Fs = abs(F);
>> figure
>> subplot(2, 1, 1);
>> plot(w, Fs);
>> axis([-2 * pi 2 * pi 0.1 1.1]);
>> grid on;
>> title('数值计算X1(jw)的幅度谱', 'FontSize', 14);
>> ylabel('|X1(jw)|');
>> xlabel('\omega/\omega_0');
>> subplot(2, 1, 2);
>> plot(w, Fe);
>> axis([-2 * pi 2 * pi -1.5 1.5]);
>> title('数值计算X1(jw)的相位谱', 'FontSize', 14);
>> grid on;
>> ylabel('∠X1(jw) (rad)');
>> xlabel('\omega/\omega_0');

（2）X2(t) 信号

>> clear all;
>> syms x;
>> f = exp(-3 * abs(x)) .* sin(2 * x);
>> F = fourier(f);
>> figure
>> Fs = abs(F);
>> Fe = angle(F);
>> subplot(2, 1, 1);
>> ezplot(Fs);
>> grid on;
>> title('符号计算X2(jw)的幅度谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('|X2(jw)|');
>> subplot(2, 1, 2);
>> ezplot(Fe);
>> fplot(Fe);
>> axis([-2 * pi 2 * pi -1.6 1.6]);
>> axis([-2 * pi 2 * pi -2 2]);
>> grid on;
>> title('符号计算X2(jw)的相位谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('∠X2(jw) (rad)');
>> clear all;
>> T = 0.01;
>> dw = 0.01;
>> t = -10 : T : 10;
>> w = -2 * pi : dw : 2 * pi;
>> f = exp(-3 * abs(t)) .* sin(2 * t);
>> F = f * exp(-j * t' * w) * T;
>> figure
>> Fs = abs(F);
>> Fe = angle(F);
>> subplot(2, 1, 1);
>> plot(w, Fs);
>> grid on;
>> axis([-2 * pi 2 * pi -0.01 0.23]);
>> title('数值计算X2(jw)的幅度谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('|X2(jw)|');
>> subplot(2, 1, 2);
>> plot(w, Fe);
>> grid on;
>> axis([-2 * pi 2 * pi -2 2]);
>> title('数值计算X2(jw)的相位谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('∠X2(jw) (rad)');

（3）X3(t) 信号

>> clear all;
>> syms x;
>> f = heaviside(x + 0.5) - heaviside(x - 0.5);
>> F = fourier(f);
>> Fs = abs(F);
>> Fe = angle(F);
>> figure
>> subplot(2, 1, 1);
>> ezplot(Fs, [-5 * pi, 5 * pi]);
>> grid on;
>> title('符号计算X3(jw)的幅度谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('|X3(jw)|');
>> subplot(2, 1, 2);
>> ezplot(Fe, [-5 * pi, 5 * pi]);
>> grid on;
>> title('符号计算X3(jw)的相位谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('∠X3(jw) (rad)');
>> clear all;
>> T = 0.01;
>> dw = 0.01;
>> t = -5 : T : 5;
>> w = -5 * pi : dw : 5 * pi;
>> f = Heaviside(t + 0.5) - Heaviside(t - 0.5);
>> F = f * exp(-j * t' * w) * T;
>> Fs = abs(F);
>> Fe = angle(F);
>> figure;
>> subplot(2, 1, 1);
>> plot(w, Fs);
>> axis([-5 * pi 5 * pi -0.1 1.1]);
>> grid on;
>> title('数值计算X3(jw)幅度谱', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('|X3(jw)|');
>> subplot(2, 1, 2);
>> plot(w, Fe);
>> plot(w, abs(Fe));
>> axis([-5 * pi 5 * pi -0.2 3.3]);
>> grid on;
>> xlabel('\omega/omega_0');
>> xlabel('\omega/\omega_0');
>> ylabel('∠X3(jw) (rad)');
>> title('数值计算X3(jw)相位谱', 'FontSize', 14);

生成的谱图：

（1）X1(t) 信号

符号计算方法：

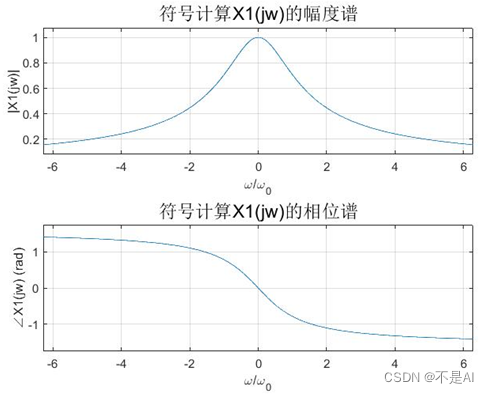
在这里插入图片描述

数值计算方法：

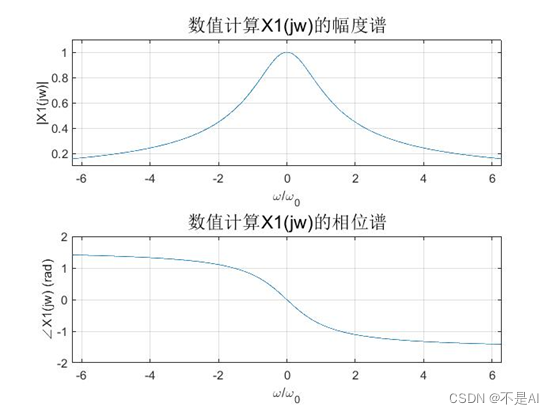
在这里插入图片描述
（2）X2(t) 信号

符号计算方法：

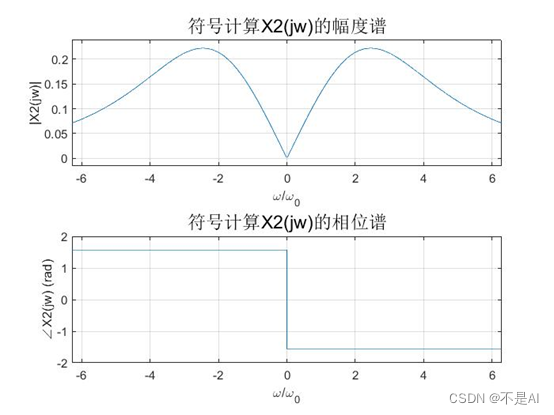
在这里插入图片描述

数值计算方法：

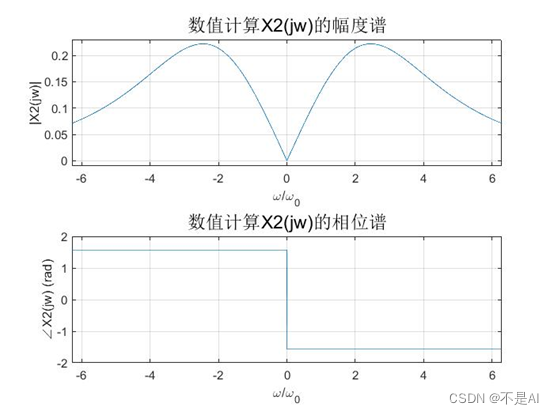
在这里插入图片描述
（3）X3(t) 信号

符号计算方法：

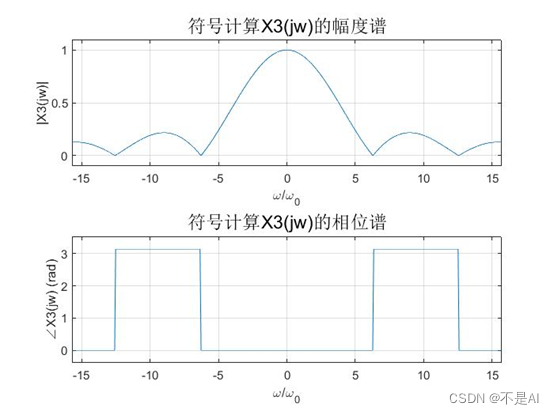
在这里插入图片描述
数值计算方法：

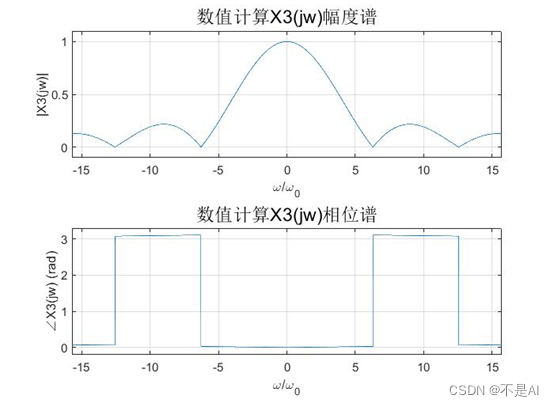
在这里插入图片描述

3、

在这里插入图片描述

（1）、验证线性性质

MATLAB代码：

>> clear all;
>> syms t;
>> x1 = exp(-t) .* heaviside(t);
>> x2 = exp(-3 * abs(t)) .* sin(2 * t);
>> x = 2 * x1 + 5 * x2;
>> X = fourier(x);
>> figure
>> subplot(2, 1, 1);
>> aX = abs(X);
>> pX = angle(X);
>> ezplot(aX);
>> grid on;
>> title('直接计算傅里叶变换的实部', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('|X(jw)|');
>> subplot(2, 1, 2);
>> ezplot(pX);
>> grid on;
>> title('直接计算傅里叶变换的虚部', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('∠X(jw) (rad)');
>> X1 = fourier(x1);
>> X2 = fourier(x2);
>> Y = 2 * X1 + 5 * X2;
>> aY = abs(Y);
>> pY = angle(Y);
>> figure
>> subplot(2, 1, 1);
>> ezplot(aY);
>> grid on;
>> title('使用性质计算傅里叶变换的实部', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('|X(jw)|');
>> subplot(2, 1, 2);
>> ezplot(pY);
>> grid on;
>> title('使用性质计算傅里叶变换的虚部', 'FontSize', 14);
>> xlabel('\omega/\omega_0');
>> ylabel('∠X(jw) (rad)');

直接计算：

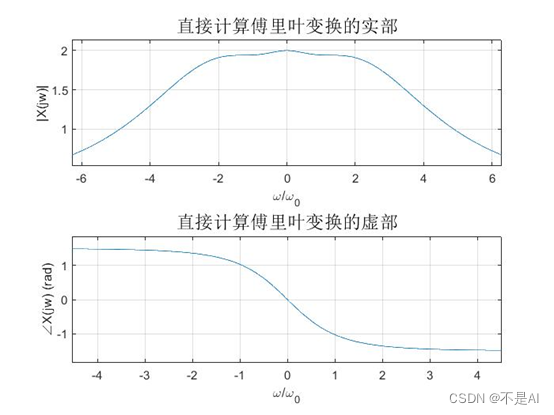
在这里插入图片描述

使用性质计算：

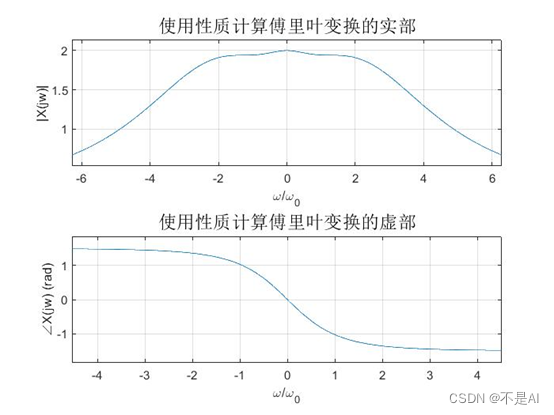
在这里插入图片描述

（2）验证卷积性质：

// 待更新。

4、

在这里插入图片描述

MATLAB代码：

signal_DTFT函数：

function X = signal_DTFT(xn, n, w)
X = xn * (exp(-1i) .^ (n' * w));

其余代码：

>> clear all;
>> w = -4 * pi : 0.01 : 4 * pi;
>> n = -30 : 30;
>> xn = 0.5 .^ (n - 1) .* (n >= 1);
>> X = signal_DTFT(xn, n, w);
>> magX = abs(X);
>> figure
>> subplot(2, 1, 1);
>> plot(w, magX);
>> grid on;
>> xlabel('\omega/\omega_0');
>> ylabel('|X(e^{jw})|');
>> title('傅里叶变换的模值', 'FontSize', 14);
>> axis([-4 * pi, 4 * pi, 0.5, 2]);
>> subplot(2, 1, 2);
>> plot(w, phaX);
>> axis([-4 * pi, 4 * pi, -4, 4]);
>> grid on;
>> xlabel('\omega/\omega_0');
>> ylabel('∠X(e^{jw}) (rad)');
>> title('傅里叶变换的相位', 'FontSize', 14);

傅里叶变换结果：

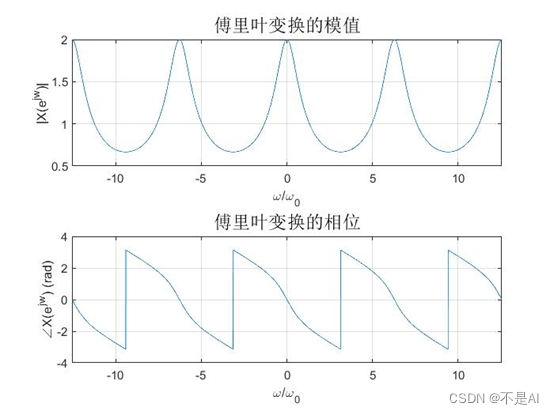
在这里插入图片描述
5、思考题

在这里插入图片描述

答： 数值计算和符号计算的精度不同。符号计算的精度取决于MATLAB中 ezplot 函数的精度，而数值计算的精度取决于自己定义的 w 变量的精度。

三、实验收获与感想：

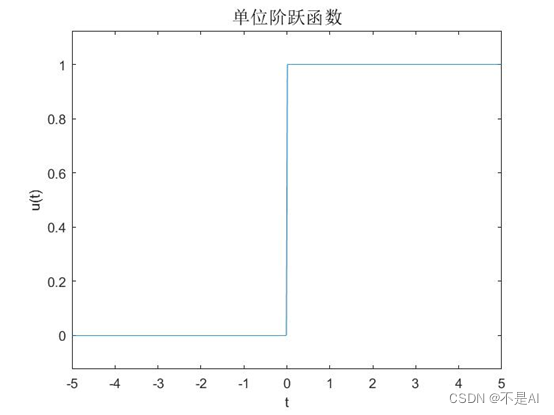
1、 单位阶跃函数 u(t) 可以用 heaviside(t) 函数近似表示。在 t = 0 时刻的函数值为 0.5. 举例：

>> clear all;
>> syms x;
>> u = heaviside(x);
>> ezplot(u, [-5, 5]);
>> xlabel('t');
>> ylabel('u(t)');
>> title('单位阶跃函数', 'FontSize', 14);
>> heaviside(0)ans =0.5000

函数图像：

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/414426.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【Flink-1.17-教程】-【三】Flink 运行架构、Flink 核心概念【并行度、算子链、任务槽】、Flink 作业提交流程

【Flink-1.17-教程】-【三】Flink 运行架构、Flink 核心概念【并行度、算子链、任务槽】、Flink 作业提交流程

【Flink-1.17-教程】-【三】Flink 运行架构、Flink 核心概念【并行度、算子链、任务槽】、Flink 作业提交流程 1）系统架构1.1.系统成员组成1.2.作业提交流程 2）核心概念2.1. 并行度（Parallelism）2.1.1.并行子任务和并行度2.1.2.并…
阅读更多...
为什么要选择“零代码”开发的智慧能源管理平台？

为什么要选择“零代码”开发的智慧能源管理平台？

全球低代码市场发展较早，集中度逐渐凸显，零代码市场尙未形成市场格局，很多企业出现“业务部门不懂技术，技术部门不懂业务”的现象往往会制约软件的开发进度，如何快速搭建软件系统应用，助力业务增长与效率提…
阅读更多...
navigateTo失效-跳转不了页面解决办法！uniapp\vue

navigateTo失效-跳转不了页面解决办法！uniapp\vue

改了一个小时多的错误，跳转页面无论怎么样都跳转不了，有2个问题： 注意：uniapp的报错可以在console里检查！ 1.pages.json文件没有配置路径， 在pages:[ ]里面加 （根据自己的路径进行修改 {&qu…
阅读更多...
Flask 项目怎么配置并创建第一个小项目？附上完成第一个小案例截图

Flask 项目怎么配置并创建第一个小项目？附上完成第一个小案例截图

目录 1. 为什么要学习 flask？ 2. flask 是什么？ 3. flask 如何使用？ 要安装 Flask，可以按照以下步骤进行： 4. 使用流程 4.1. 新建项目 4.1.1. 打开 pycharm，新建项目 4.1.2. 设置目录，并…
阅读更多...
elastic search入门

elastic search入门

参考1：Elastic Search 入门 - 知乎 参考2：Ubuntu上安装ElasticSearch_ubuntu elasticsearch-CSDN博客 1、ElasticSearch安装 1.1安装JDK，省略，之前已安装过 1.2创建ES用户 创建用户：sudo useradd esuser 设置密码&…
阅读更多...
ICCV2023 | PTUnifier+：通过Soft Prompts(软提示)统一医学视觉语言预训练

ICCV2023 | PTUnifier+：通过Soft Prompts(软提示)统一医学视觉语言预训练

论文标题：Towards Unifying Medical Vision-and-Language Pre-training via Soft Prompts 代码：https://github.com/zhjohnchan/ptunifier Fusion-encoder type和Dual-encoder type。前者在多模态任务中具有优势，因为模态之间有充分的相互…
阅读更多...
CentOS 8.5 安装图解

CentOS 8.5 安装图解

特特特别的说明 CentOS发行版已经不再适合应用于生产环境，客观条件不得不用的话，优选7.9版本，8.5版本次之，最次6.10版本（比如说Oracle 11GR2就建议在6版本上部署）！ 引导和开始安装 选择倒计时结…
阅读更多...
Spring使用注解管理Bean

Spring使用注解管理Bean

引入lib包 Spring对Bean管理的常用注解 Component组件(作用在类上) Spring中提供了Component的三个衍生注解:(功能在目前为止是一致的) Controller WEB层 Service 业务层 Repository 持久层 属性注入的注解:(使用注解注入的方式,可以不用提供set方法) Value 用于注入普…
阅读更多...
看透繁花，六大经典台词另有深意

看透繁花，六大经典台词另有深意

（图源：《繁花》官方微博） 大火的《繁花》，大家看了吗？ 变迁的时代，裹挟着市井万象，多舛的命运，缩影了“繁花“时代向前的潮涌潮落。 同在变革的大潮，《繁花》里“上帝…
阅读更多...
allegro画PCB如何设置原点

allegro画PCB如何设置原点

如上图，然后鼠标点击那里，原点就在哪，如果那个位置点不上，就可能超出了你底板的范围，需要设置加大底板面积，设置底板大小的方法如下： 链接: link
阅读更多...
Asp.Net期末课程设计——任务展示系统（C#）（mysql或sqlserver）

Asp.Net期末课程设计——任务展示系统（C#）（mysql或sqlserver）

前言 声明：该文章只是做技术分享，若侵权请联系我删除。！！ 感谢大佬的视频： https://www.bilibili.com/video/BV1664y1P7VT/?vd_source5f425e0074a7f92921f53ab87712357b 源码：https://space.bilibili.co…
阅读更多...
teracopy下载 3.17版本

teracopy下载 3.17版本

最新版本更新时间：2023 年 12 月 3 日 更新日志： 克隆和重新扫描功能。 添加了对 SSE2 处理器的 xxHash 支持。 升级了报告和校验和导出功能。 在测试和验证过程中实现了网络恢复等待功能。 将最大缓冲区容量扩展到 256 MB。 解决了一些小错误并改…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023