DNN是指深度神经网络,它是一个很广的概念,某种意义上CNN、RNN、GAN等都属于其范畴之内。DNN与CNN([卷积神经网络)的区别是DNN特指全连接的神经元结构,并不包含卷积单元或是时间上的关联。其中最初的神经网络的所有隐含层都是全连接的,这也就导致其计算量巨大!!!一度无法加深网络,并且在网络加深之后训练起来更容易进入局部最优解,很难优化!
神经网络的发展史:
1,感知机(M-P模型)
神经网络技术起源于上世纪五、六十年代,当时叫感知机(perceptron),拥有输入层、输出层和一个隐含层。输入的特征向量通过隐含层变换达到输出层,在输出层得到分类结果。早期感知机的推动者是Rosenblatt。但是,Rosenblatt的单层感知机有一个严重得不能再严重的问题,对于计算稍微复杂的函数其计算力显得无能为力。
2,多层感知机(MLP模型)
随着数学的发展,这个缺点直到上世纪八十年代才被Rumelhart、Williams、Hinton、LeCun等人发明的多层感知机(multilayer perceptron)克服。多层感知机,顾名思义,就是有多个隐含层的感知机。多层感知机可以摆脱早期离散传输函数的束缚,使用sigmoid或tanh等连续函数模拟神经元对激励的响应,在训练算法上则使用Werbos发明的反向传播BP算法。对,这就是我们现在所说的神经网络( NN)!多层感知机解决了之前无法模拟异或逻辑的缺陷,同时更多的层数也让网络更能够刻画现实世界中的复杂情形。多层感知机给我们带来的启示是,神经网络的层数直接决定了它对现实的刻画能力——利用每层更少的神经元拟合更加复杂的函数。
即便大牛们早就预料到神经网络需要变得更深,但是有一个梦魇总是萦绕左右。随着神经网络层数的加深,优化函数越来越容易陷入局部最优解,并且这个“陷阱”越来越偏离真正的全局最优。利用有限数据训练的深层网络,性能还不如较浅层网络。同时,另一个不可忽略的问题是随着网络层数增加,“梯度消失”现象更加严重。具体来说,我们常常使用 sigmoid 作为神经元的输入输出函数。对于幅度为1的信号,在BP反向传播梯度时,每传递一层,梯度衰减为原来的0.25。层数一多,梯度指数衰减后低层基本上接受不到有效的训练信号。
3,深度神经网络(DNN)
2006年,Hinton利用预训练方法缓解了局部最优解问题,将隐含层推动到了7层(参考论文:Hinton G E, Salakhutdinov R R. Reducing the Dimensionality of Data with Neural Networks[J]. Science, 2006, 313(5786):504-507.),神经网络真正意义上有了“深度”,由此揭开了深度学习的热潮。这里的“深度”并没有固定的定义——在语音识别中4层网络就能够被认为是“较深的”,而在图像识别中20层以上的网络屡见不鲜。为了克服梯度消失,ReLU、maxout等传输函数代替了 sigmoid,形成了如今 DNN 的基本形式。
4,卷积神经网络(CNN)
我们看到全连接DNN的结构里下层神经元和所有上层神经元都能够形成连接,带来的潜在问题是参数数量的膨胀。假设输入的是一幅像素为1K*1K的图像,隐含层有1M个节点,光这一层就有10^12个权重需要训练,这不仅容易过拟合,而且极容易陷入局部最优。另外,图像中有固有的局部模式(比如轮廓、边界,人的眼睛、鼻子、嘴等)可以利用,显然应该将图像处理中的概念和神经网络技术相结合。此时我们可以祭出题主所说的卷积神经网络CNN。对于CNN来说,并不是所有上下层神经元都能直接相连,而是通过“卷积核”作为中介。同一个卷积核在所有图像内是共享的,图像通过卷积操作后仍然保留原先的位置关系。
对于图像,如果没有卷积操作,学习的参数量是灾难级的。CNN之所以用于图像识别,正是由于CNN模型限制了参数的个数并挖掘了局部结构的这个特点。顺着同样的思路,利用语音语谱结构中的局部信息,CNN照样能应用在语音识别中。在普通的全连接网络或CNN中,每层神经元的信号只能向上一层传播,样本的处理在各个时刻独立,因此又被称为前向神经网络(Feed-forward Neural Networks)。
深度神经网络的示例图如下,其中每一层都是全连接层,这也导致其计算量极其复杂!

卷积神经网络的示例图如下,其中通过映入卷积核的概念来大幅度减少计算量,并且在整个网络中,每层的神经元与卷积核共享权值
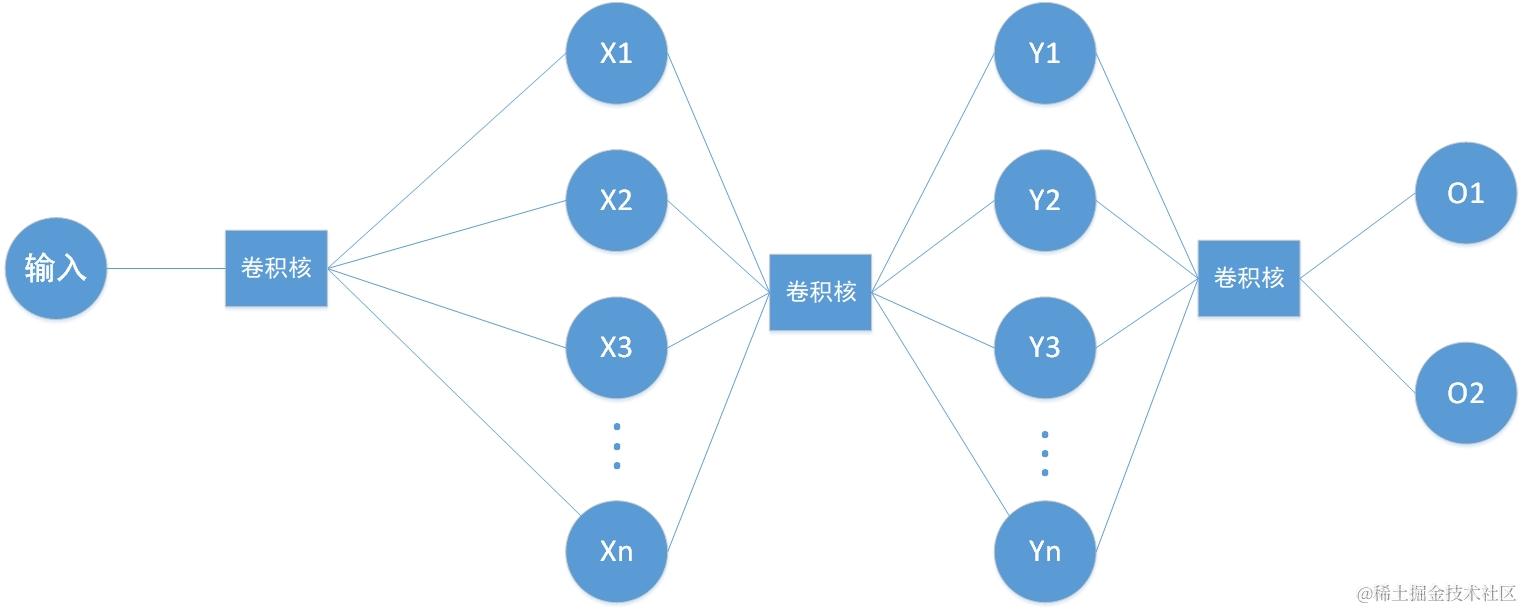
其中卷积神经网络中的神经元个数计算方式为输出特征图的像素点个数(即H* W *C),举例:
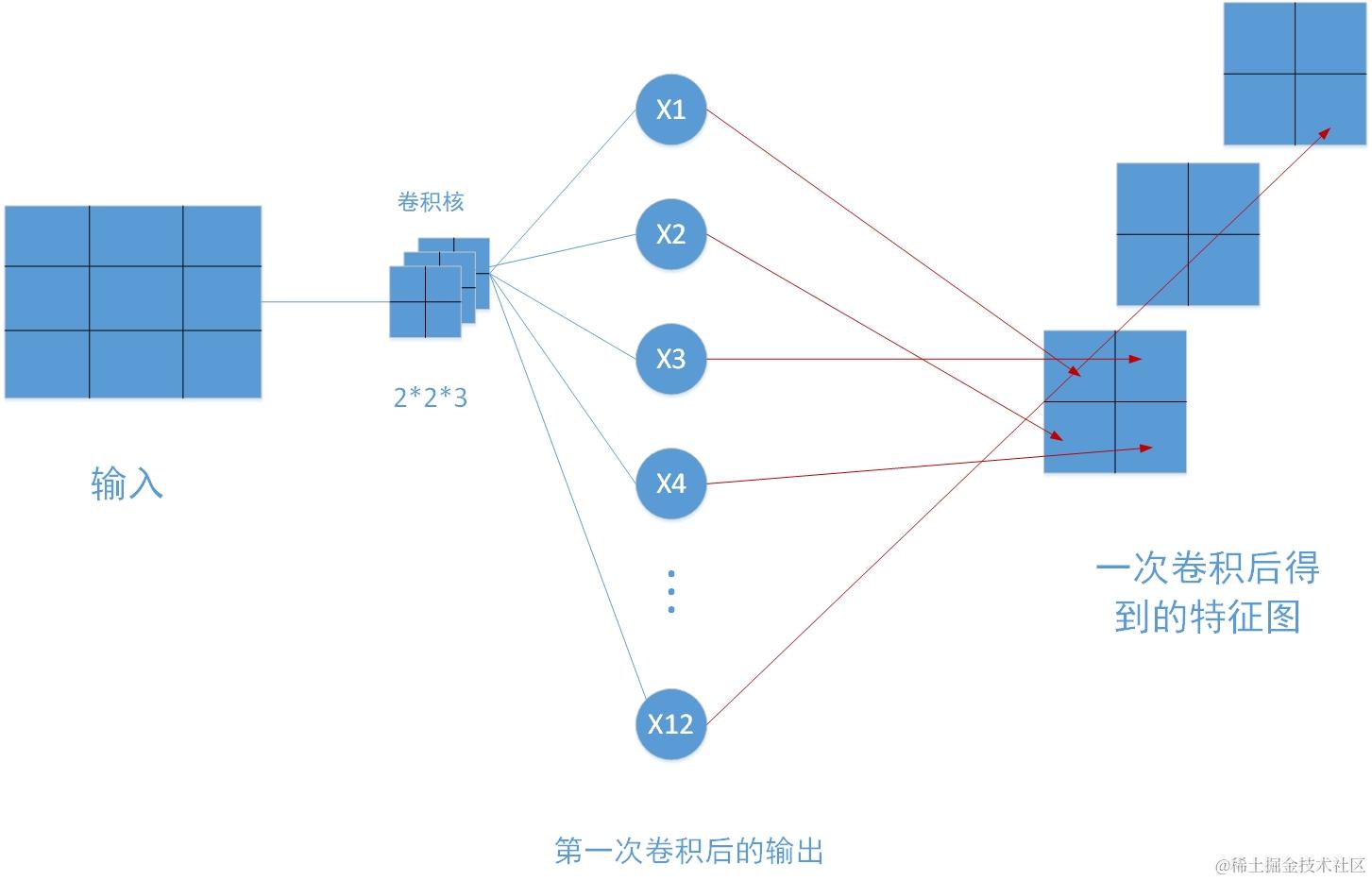
如上所示,在对一张4 * 4大小尺寸的灰度图使用卷积核大小为2 *2 *3一次卷积后会得到一张新的特征图,其中新的特征图中的每个像素点都对应着一个神经元,卷积核大小为3,因此新的特征图的通道数为3,总共的像素点个数=神经元数量=2 *2 *3=12个。