一、题目
假设你是一所大学的行政管理人员,你想根据两门考试的结果,来决定每个申请人是否被录取。你有以前申请人的历史数据,可以将其用作逻辑回归训练集。对于每一个训练样本,你有申请人两次测评的分数以及录取的结果。为了完成这个预测任务,我们需要构建一个可以基于两次测试评分来评估录取可能性的分类模型。
二、可视化数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('ex2data1.txt', names=['exam1', 'exam2', 'admitted'])
print(data.head()) 
print(data.describe())
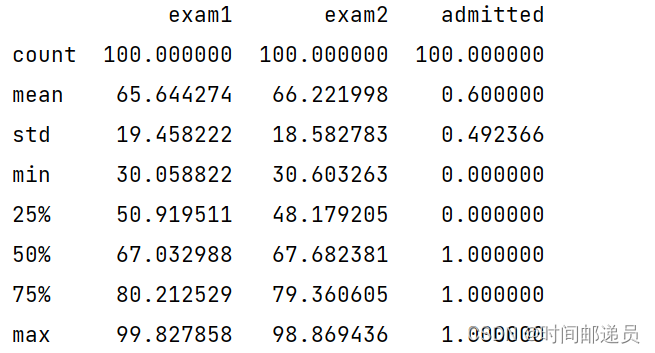
让我们创建两个分数的散点图,并使用颜色编码来可视化,如果样本是正的(被录取)或负的(未被录取)
# 具体来说,data.admitted表示data DataFrame中的admitted列
# isin([1])是一个布尔条件,用于检查admitted列中的值是否在列表[1]中
# data[data.admitted.isin([1])]表示从data DataFrame中筛选出满足条件的行
# 最后,将筛选出的行赋值给变量positive
positive = data[data.admitted.isin([1])] # 1
negative = data[data.admitted.isin([0])] # 0 fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
# marker='x':这表示点的标记样式为叉号
ax.scatter(negative['exam1'], negative['exam2'], s=50, c='r', marker='x', label='Not Admitted')
# 设置横纵坐标名
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show() 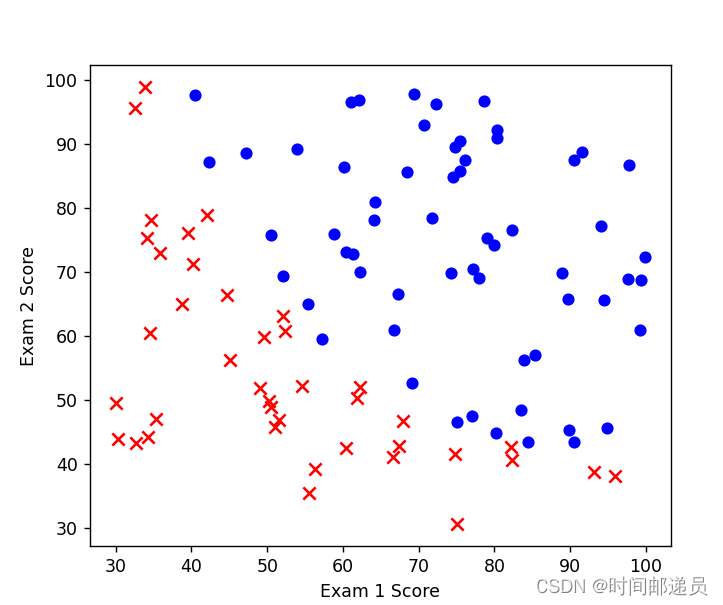
三、 Sigmoid function
根据前面我们给出的的假设函数和g函数
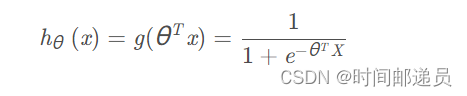
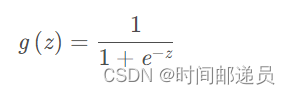
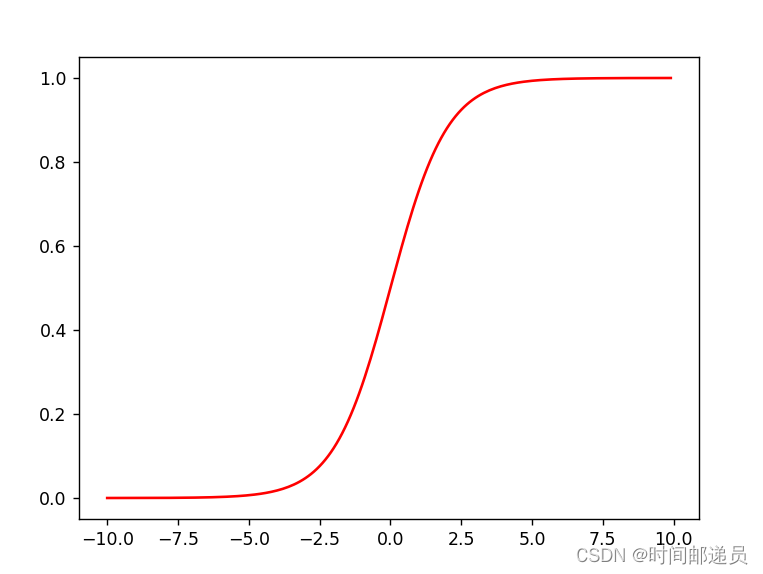
def sigmoid(z): return 1 / (1 + np.exp(- z)) x1 = np.arange(-10, 10, 0.1)
plt.plot(x1, sigmoid(x1), c='r')
plt.show()
四、代价函数
代价函数的表达式前面我们也讲过:
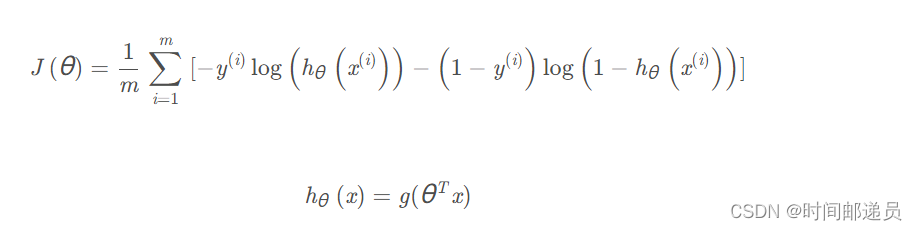
def cost(theta, X, y): theta = np.matrix(theta) first = np.multiply(-y, np.log(sigmoid(X * theta.T))) second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T))) return np.sum(first - second) / (len(X)) 获取训练集的数据并传入参数计算Cost
data.insert(0, 'Ones', 1)
cols = data.shape[1]
X = data.iloc[:, 0:cols - 1]
y = data.iloc[:, cols - 1:cols]
print(X.head())
print(y.head())
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.zeros(3)
print(cost(theta, X, y)) # 0.6931471805599453 五、批量梯度下降
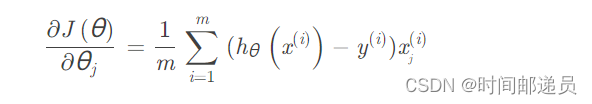
def gradient(theta, X, y): theta = np.matrix(theta) grad_theta = np.array(((X.T) @ (sigmoid(X @ theta.T) - y)) / len(X)).reshape(-1) return grad_theta grad_theta = gradient(theta, X, y)
print(type(grad_theta))
print(grad_theta) #[ -0.1 -12.00921659 -11.26284221] 六、训练参数θ
注意,我们实际上没有在上面的函数中执行梯度下降,我们仅仅在计算梯度。由于我们使用Python,我们可以用SciPy的optimize来计算成本和梯度参数。这里我们使用的是高级优化算法,运行速度通常远远超过梯度下降,方便快捷,我们只需传入cost函数、初始化的变量theta、X、y和梯度即可
import scipy.optimize as optresult = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
print(result) # (array([-25.16131859, 0.20623159, 0.20147149]), 36, 0)
print(cost(result[0], X, y)) # 0.20349770158947475 七、训练模型
训练好了参数θ后,我们来用这个模型预测某个学生是否能被录取。接下来,我们需要编写一个函数,用我们所训练的参数θ来为数据集X输出预测,然后我们可以使用这个函数来给我们的分类器的训练精度打分。
逻辑回归模型的假设函数:
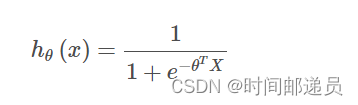
当大于等于0.5时,预测 y=1
当小于0.5时,预测 y=0
def predict(theta, X): theta = np.matrix(theta) probability = sigmoid(X * theta.T) return [1 if x >= 0.5 else 0 for x in probability] final_theta = result[0]
predictions = predict(final_theta, X)
print(predictions)
correct = [1 if a == b else 0 for (a, b) in zip(predictions, y)]
print(correct)
accuracy = sum(correct) / len(X)
print(accuracy) #0.89 可以看到我们预测精度达到了89%
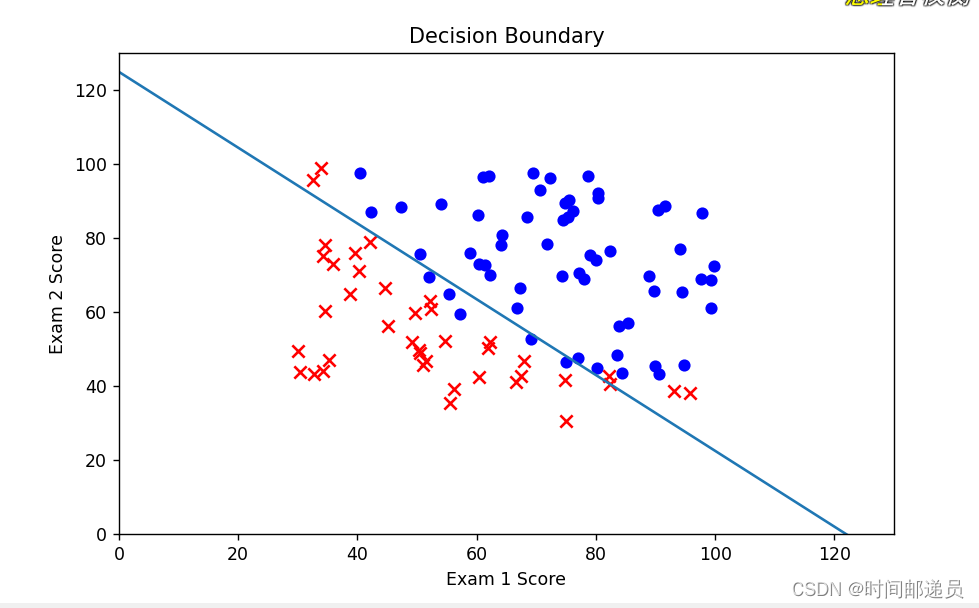
八、决策边界

x1 = np.arange(130, step=0.1)
x2 = -(final_theta[0] + x1 * final_theta[1]) / final_theta[2]
fig, ax = plt.subplots(figsize=(8, 5))
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
ax.scatter(negative['exam1'], negative['exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x1, x2)
ax.set_xlim(0, 130)
ax.set_ylim(0, 130)
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
ax.set_title('Decision Boundary')
plt.show()