“有六个条幅（等宽），每个着以红色、白色或蓝色，把这些条幅连成一面长条旗，这种旗子有多少种？”*

1	1	1	1	1	2
2	1	1	1	1	1

如果旗子的颜色镜像对称视为同一种

按照“（伯恩赛德引理）设G是一个作用在有限集合X上的有限群，令N为轨道的个数，则

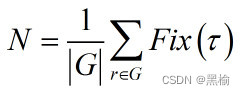
其中Fix(x)是被τ固定的x∈X的个数.”*

旗子的数量为

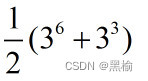
共有378种不同的组合

条幅	颜色		数量		排列组合	回文		数量
6	3		378		729	27		378
6	2		36		64	8		36
4	3		45		81	9		45
4	2		10		16	4		10

用同样的方法计算如果是6个条幅，2个颜色可能的组合为36个。如果有4个条幅2个颜色，不同的着色方法只有10个，分别是

1		1	1	1	1
2		1	1	1	2
3		1	1	2	1
4		1	1	2	2
5		1	2	1	2
6		1	2	2	1
7		1	2	2	2
8		2	1	1	2
9		2	1	2	2
10		2	2	2	2

计算方法为

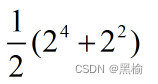
1	1	1	1
1	1	1	2		2	1	1	1
1	1	2	1		1	2	1	1
1	1	2	2		2	2	1	1
1	2	1	2		2	1	2	1
1	2	2	1
1	2	2	2		2	2	2	1
2	1	1	2
2	1	2	2		2	2	1	2
2	2	2	2

用排列组合的方法可以得到16个结构，但这16个结构里有4个

1	1	1	1
1	2	2	1
2	1	1	2
2	2	2	2

是回文的构造，他们的镜像就是本身，所以这4个结构要计算2次。

所以如果是4个条幅，3个颜色就是（81+9）/2.因为有9个回文结构

1		1	1	1	1
2		1	2	2	1
3		1	3	3	1
4		2	1	1	2
5		2	2	2	2
6		2	3	3	2
7		3	1	1	3
8		3	2	2	3
9		3	3	3	3

现在改变计算的方法，颜色可以横向移动

1	1	1	2
1	1	2	1

这两个算作同一种着色方法，计算有多少种旗子。

1		1	1	1	1	1
2		1	1	1	2	2
3		1	1	2	1	2
4		1	2	1	1	2
5		2	1	1	1	2
6		1	1	2	2	3
7		1	2	2	1	3
8		2	2	1	1	3
9		2	1	1	2	3
10		1	2	1	2	4
11		2	1	2	1	4
12		1	2	2	2	5
13		2	1	2	2	5
14		2	2	1	2	5
15		2	2	2	1	5
16		2	2	2	2	6

只有6种。但是

1		1	1	1	1
16		2	2	2	2

结构1和16在左移的操作下，4个结构是一样的，所以需要加上6.同样

6

1

2

1

2

结构6左移只有2个状态，这里少计算了2个需要再加2。所以总的着色方法为

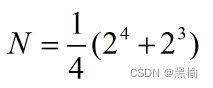
据伯恩赛德引理。着色数就是有限群G作用在有限集合X上的轨道数。一个着色就是一条轨道。

现在把1换成0，2换成1

0	0	0	0	1
0	0	0	1	2
0	0	1	1	3
0	1	0	1	4
0	1	1	1	5
1	1	1	1	6

( A, B )---1*30*2---( 1, 0 )( 0, 1 )

做一个二值化的神经网络分类A和B，让B全是0.A只有4张图片这个网络最多只能有6个不同的差值结构。所以这种神经网络的差值结构数量问题等同于在左移的操作下，用两个颜色染色横向条幅的问题。差值结构的数量就是轨道的数量,具体值可用伯恩赛德引理严格算出。

*高等近世代数 Joseph J. Rotman P78