- 669. 修剪二叉搜索树

class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null) {return null;}if (root.val < low) {return trimBST(root.right, low, high);}if (root.val > high) {return trimBST(root.left, low, high);}// root在[low,high]范围内root.left = trimBST(root.left, low, high);root.right = trimBST(root.right, low, high);return root;} }本题的关键是要明白删除节点,不能直接返回null,要考虑如果是小于low的话,要考虑删除节点的右子树,如果大于high的话,要考虑删除节点的左子树。
- 108.将有序数组转换为二叉搜索树

class Solution {public TreeNode sortedArrayToBST(int[] nums) {return sortedArrayToBSTHelper(nums,0,nums.length);}public TreeNode sortedArrayToBSTHelper(int[] nums, int begin , int end){if(begin == end) return null;int middle = (begin+end)/2;TreeNode root = new TreeNode(nums[middle]); root.left = sortedArrayToBSTHelper(nums, begin, middle);root.right = sortedArrayToBSTHelper(nums, middle+1, end);return root;} }本题相对比较简单,关键是思考清楚begin和end的开闭情况。
-
思路:每次取中间的值作为父节点,然后遍历middle左边的区间和右边的区间。
- 538.把二叉搜索树转换为累加树
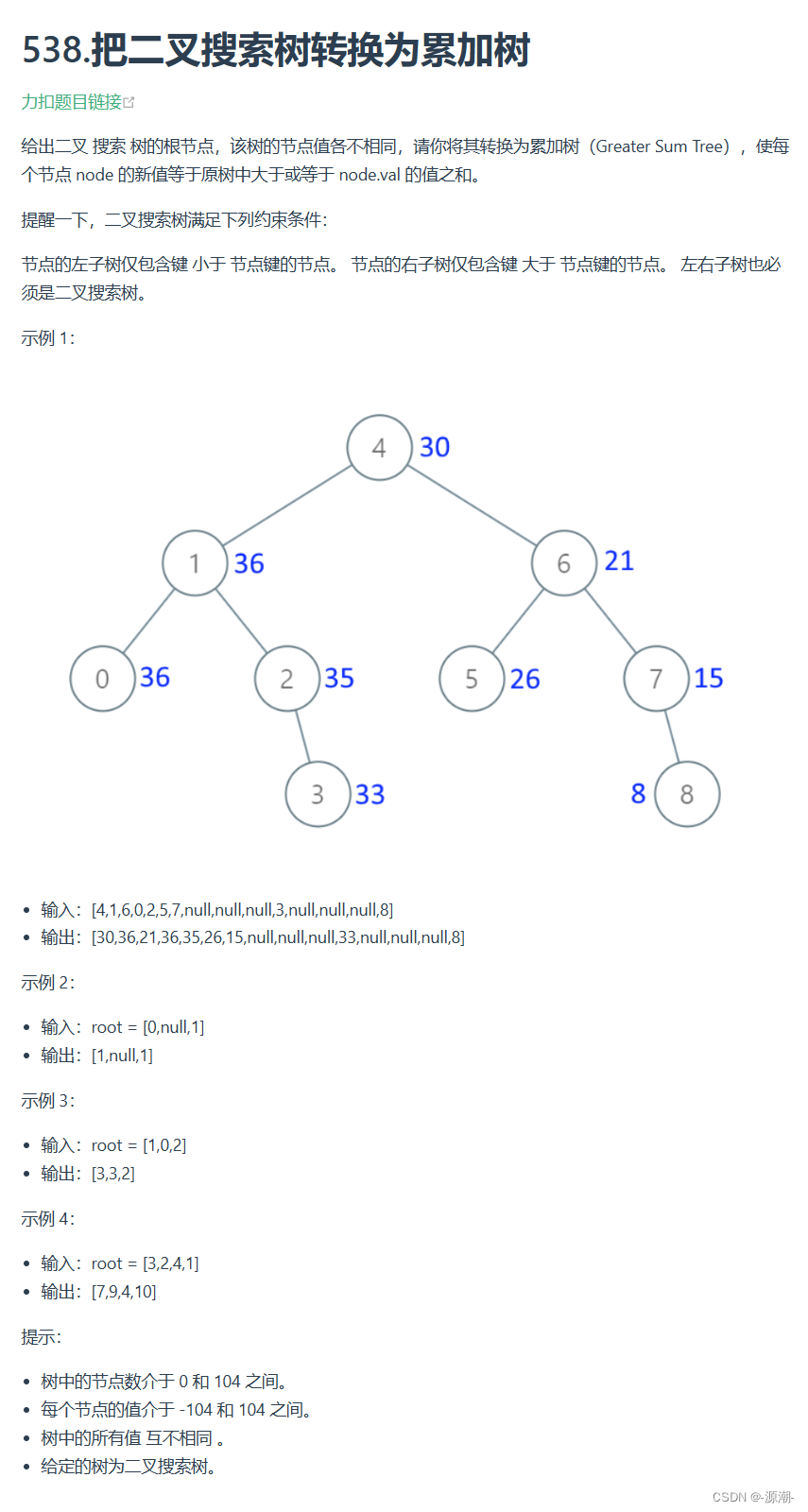
class Solution {int sum;public TreeNode convertBST(TreeNode root) {sum = 0;convertBST1(root);return root;}// 按右中左顺序遍历,累加即可public void convertBST1(TreeNode root) {if (root == null) {return;}convertBST1(root.right);sum += root.val;root.val = sum;convertBST1(root.left);} }思路:本题的关键是右中左的遍历顺序,用一个指针sum记录前一个节点的值,与当前节点相加。
- 总结篇