题目链接
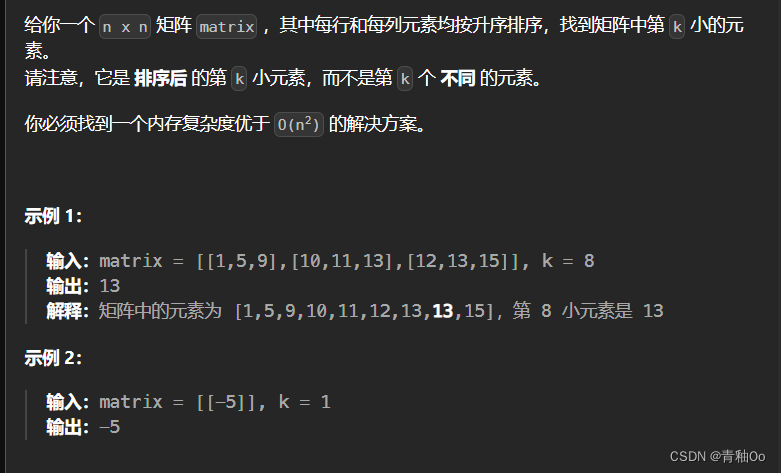
有序矩阵中第 K 小的元素
题目描述
注意点
- 每行和每列元素均按升序排序
- 找到一个内存复杂度优于 O(n²) 的解决方案
解答思路
- 使用二分查找,思路为:
(1)因为左上角的元素值更小,右下角的元素值更大,先将left设置为左上角元素的值,right设置为右下角元素的值;
(2)判断不大于left和right中间值mid的元素数量sum;
(3)如果sum小于k,则将left设置为mid + 1,否则将right设置为mid。 - 不断重复上述过程,直到满足sum等于k时right的最小值,此时left等于right,且right是大于等于矩阵中K个元素的临界点,所以矩阵中一定会有一个元素等于right(否则说明并没有找到sum等于k时right的最小值),right也就是有序矩阵中第 K 小的元素
代码
class Solution {int n;public int kthSmallest(int[][] matrix, int k) {n = matrix.length;int left = matrix[0][0];int right = matrix[n - 1][n - 1];while (left < right) {int mid = left + (right - left) / 2;int sum = countLessThanMid(matrix, mid);if (sum < k) {left = mid + 1;} else {right = mid;}}return left;}public int countLessThanMid(int[][] matrix, int mid) {int sum = 0;for (int i = 0; i < n; i++) {// 如果左上角都大于mid,则一定没有小于等于mid的元素存在if (matrix[i][0] > mid) {return sum;}// 如果右上角都小于等于mid,则该行所有元素都小于等于midif (matrix[i][n - 1] <= mid) {sum += n;continue;}// 其余情况查找改行小于等于mid的元素for (int j = 0; j < n; j++) {if (matrix[i][j] > mid) {break;}sum++;}}return sum;}
}
关键点
- 二分查找的思路
- 怎么找到sum等于k时right的最小值
- 当right - left=1,且两个数都是负数的时候,求mid时会等于right的值,此时如果sum >= k,则会一直卡在循环中无法跳出,需要保证这种特殊情况求mid也是left,所以求mid时使用left + (right - left) / 2