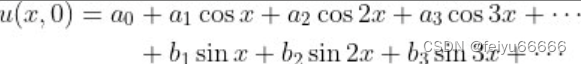主要是课堂的补充(yysy,我觉得课堂的教育模式真有够无聊的,PPT、写作业、考试,感受不到知识的魅力。
它告诉我们什么?
空间和时间中的任何模式都可以被看作不同频率的正弦模式的叠加。
为什么重要?
频率分量可用于分析模式、定制模式、提取重要特征,以及消除随机噪声。
它带来了什么?
傅里叶的技巧应用极为广泛,比如图像处理和量子力学。它用于发现DNA等大型生物分子的结构、压缩数码照片中的图像数据、清理古老或损坏的录音,以及分析地震。现代技术用于高效地存储指纹数据和改进医疗扫描仪。
傅里叶的热方程
在波动方程之后,很快就出现了非常相似的引力、静电、弹性和热流方程。许多方程都用发明者的名字命名:拉普拉斯方程、泊松方程。关于热的方程则没有用人名命名,这个方程的名字缺乏想象力,还不完全准确——“热方程”。它由约瑟夫·傅里叶(Joseph Fourier)提出,而他的思想引出一个新的数学领域,其影响远远超出了问题最初的来源。波动方程本来也可能引出这一思想,类似的方法在人们的数学意识中早有浮现,但历史却选择了热学。
这种新方法有一个前途光明的开端:1807年,傅里叶根据一个新的偏微分方程向法国科学院提交了一篇关于热流的文章。虽然这所著名的机构拒绝发表文章,但它鼓励傅里叶进一步研究他的思想并再试一次。当时,科学院有一个年度研究奖项,颁发给他们认为足够有趣的任何主题。他们选择热学作为1812年奖项的主题。傅里叶正式提交了他经过修订和扩充的文章,并赢得了奖项。他的热方程是这样的:
这里的u(x,t)是一根金属杆在时刻t、位置x处的温度,其中杆无限细,α是一个常数,指热扩散率。所以它真的应该被称为温度方程。他还给出了一个更高维的版本:
,对平面或空间中的任何指定区域都成立。
热方程与波动方程惊人地相似,但有一处重要的区别。波动方程用的是对时间的二阶导数
,但到了热方程里则变成了一阶导数
。这个区别可能看起来很小,但其物理意义是巨大的。和会永远振动的小提琴琴弦不同(根据波动方程,假设没有摩擦或其他阻尼),热量并不会无限期持续存在。相反,随着时间的推移,热量会耗散衰减,除非有热源可以给它补充热量。因此,一个典型的问题可能是这样的:加热杆的一端以保持其温度恒定,冷却另一端并同样保持恒定,求出杆达到稳定状态后温度如何分布。答案是以指数方式下降。另一个典型的问题是,指定沿杆的初始温度分布,然后问这个分布随时间如何变化。也许开始时左半部分温度高,右半部分温度低。这个方程就会告诉我们高温部分的热量如何扩散到低温的部分。
傅里叶热方程的解法
傅里叶的获奖回忆录中最有趣的部分并不是这个方程,而是他如何求解它。如果初始分布是一个三角函数,例如sinx,则方程(对那些有处理此类问题的经验的人来说)很容易求解,答案是
。这和波动方程的基模有些相似,但那个公式是sinctsinx。琴弦的永恒振荡对应的sinct因子被指数代替,并且指数-αt中的负号告诉我们,整体温度分布沿着杆以相同的速率衰减。(这里的物理差异是波会保存能量,但热流不会。)类似地,比如对于sin5x的初始分布,解是
:同样会消失,但速度快得多。要求解热方程,只要乘上
就行了。
接下来,故事大体上就和波动方程差不多了。热方程是线性的,因此我们可以把解叠加起来。如果初始分布是
,那么解就是
,并且两种模以不同的速率衰减。
但像这样的初始分布有点儿刻意。为了解决我在前面提到的问题,我们想要这样一个初始分布:其中杆有一半是u(x,0)=1,另一半是-1。这样的分布是不连续的,用工程术语来说叫作“方波”。但正弦和余弦曲线是连续的。因此,正弦和余弦曲线的任何叠加都不能代表方波。
当然,任何有限的叠加都不行。但是,如果我们允许无穷多项呢?那么我们可以尝试将初始分布表示为一个无穷级数,形如
其中a0,a1,a2,a3…、b0,b1,b2,b3…是合适的常数(因为sin0x=0,所以没有b0)。现在看来有可能得到方波了。实际上,大多数系数可以设为零。只有n为奇数的bn需要保留,并且
。
傅里叶甚至给出了一般分布f(x)的系数an和bn的积分通项公式:
在经历了对三角函数进行幂级数展开的周折之后,他意识到还有简单得多的方法可以推导出这些公式。如果你取两个不同的三角函数,比如cos2x和sin5x,将它们相乘,并从0到2
积分,就会得到零。哪怕它们看起来是cos5x和sin5x也是一样。但如果两个函数是相同的,比如都是sin5x,那积分就不是零——实际上是
。如果你设f(x)是三角级数的和,将所有数字乘以sin5x并积分,则所有项都会消失,除了对应于sin5x的那一项,即b5sin5x。这一项的积分结果是
。那么除以
之后就得出了b5项的傅里叶公式。所有其他系数也是如此。
傅里叶解法的问题
正如我们在第8章中看到的那样,欧拉和伯努利多年来一直就波动方程争论类似问题,只不过方程里不是傅里叶提出的随时间的指数耗散,而是波幅的无限正弦振荡。背后的数学问题是同一个。事实上,欧拉已经针对波动方程发表了系数的积分公式。
然而,欧拉从未说过该公式适用于不连续函数f(x),这是傅里叶的工作中最具争议的一点。无论如何,小提琴琴弦的模型并不涉及不连续的初始条件——那样的话,模型将是一根断掉的弦,根本不会振动。但是对于热来说,考虑将杆的一个区域保持在一个温度,而让相邻区域保持在另一个温度是很自然的。实际的过渡将是平滑且非常陡峭的,但是不连续的模型也是合理且更便于计算的。事实上,热方程的解就解释了为什么过渡会迅速变得平滑且非常陡峭,因为热量会横向扩散。因此一个欧拉不需要担心的问题变得无可避免,而这让傅里叶遭了殃。
数学家开始意识到无穷级数是个危险的东西。它们并不总是好好表现为有限和。最终,这些纠结的复杂性得到了解决,但这用到了一个新的数学观,花费了一百年的艰苦努力。在傅里叶的时代,每个人都觉得自己已经了解了积分、函数和无穷级数是什么,但实际上这些理解都很模糊——“我看到它的时候就认得。”因此,当傅里叶提交他的划时代论文时,科学院的官员有充分的理由保持警惕。他们拒绝让步,所以1822年,傅里叶通过出版《热解析理论》(Théorie analytique de la chaleur)一书来绕过他们的反对。1824年,傅里叶出任科学院秘书,狠狠打了批评者一耳光,并在科学院声誉卓著的期刊上发表了他1811年的原版回忆录,不刊一字。
我们现在知道,虽然傅里叶在精神上是正确的,但他的批评者也有充分的理由担心严谨性。问题很微妙,答案也不是非常直观。我们现在所谓的“傅里叶分析”非常好用,但它涉及傅里叶没有意识到的深层问题。
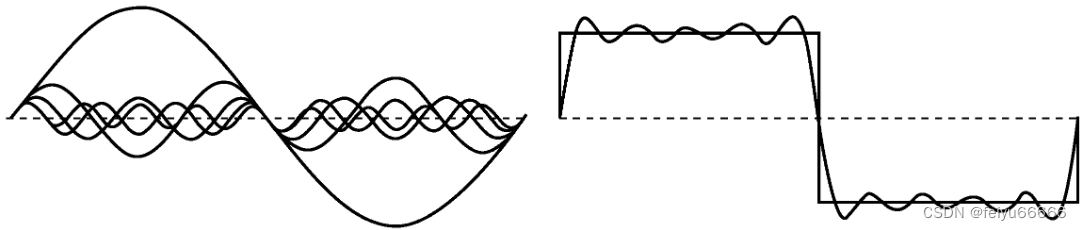
问题似乎是:傅里叶级数什么时候会收敛到自己要代表的那个函数?也就是说,取的项越多,函数就近似得更好吗?甚至连傅里叶都知道,答案并不是“一定会”。它似乎是“通常会,但在不连续点处可能出现问题”。例如,在温度跃变的中点,方波的傅里叶级数是收敛的——但数字错了。级数和是0,但方波取值为1。
对于大多数物理应用而言,在一个孤立点改变了函数值无关紧要。经过修改的方波看起来仍然是方的。它只是在不连续性上稍有区别。对傅里叶来说,这种问题并不重要。他当时正在对热流进行建模,不介意模型是否有点儿刻意,或者是否需要做些对最终结果没有重大影响的技术性改动。但是,收敛问题不能轻易被忽略,因为函数可能具有比方波更复杂的不连续性。
然而,傅里叶声称他的方法适用于任何函数,所以它甚至应该适用于这样的函数:当x是有理数时f(x)=0,当x是无理数时则f(x)=1。这个函数到处都是不连续的。当时对于这样的函数,人们甚至不清楚积分意味着什么,结果人们发现这才是争议的真正原因。没有人定义积分是什么,至少没有人定义像这样的奇怪函数。更糟糕的是,没有人定义函数是什么。即使你清理了那些遗漏的情况,这个问题也不仅仅关于傅里叶级数是否收敛。真正的困难在于理解它在什么意义下收敛。
这些问题解决起来很棘手。它需要一种由亨利·勒贝格(Henri Lebesgue)提出的新的积分理论、由格奥尔格·康托尔(Georg Cantor)从集合理论的角度重新设计的数学基础(还惹出了一堆新的麻烦)、来自黎曼等巨匠的重要见解,还需要一点儿20世纪的抽象来解决收敛问题。最终的结论是,利用正确的解释,傅里叶的想法可以变得很严谨。它适用于非常广泛但并不普遍的一类函数。级数是否对所有的x值都会收敛到f(x)并不是完全正确的提法;只要在一种特定的技术意义下,不收敛的x的值足够罕见就万事大吉了。如果函数是连续的,则级数会对任何x收敛。在跃变不连续处,如方波从1到-1跃变时,级数会非常平等地收敛到紧邻跃变任一侧处的平均值。有了对“收敛”正确的解释,级数确实总是会收敛到函数。它是作为一个整体收敛,而不是逐点收敛。如果要严格说明这一点,需要找到合适的方式来衡量两个函数之间的距离。有了这一切之后,傅里叶级数确实解决了热方程。但它真正的意义远不止于此,纯数学之外的主要受益者不是热物理学,而是工程学,特别是电子工程学。
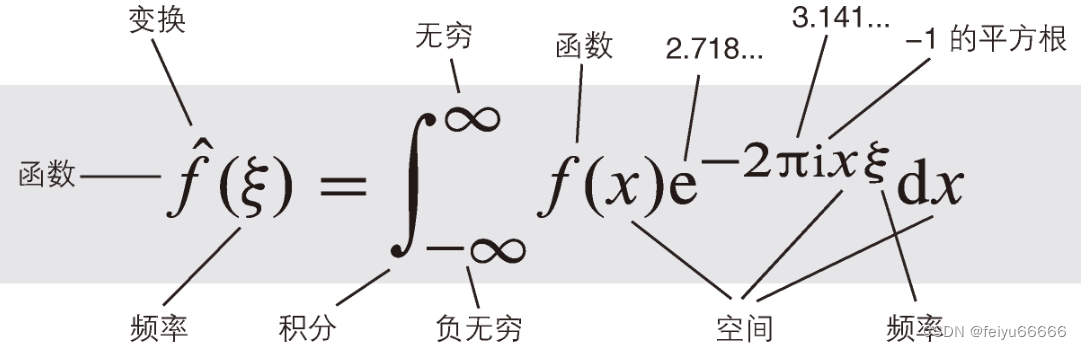
信号与通信系统
在其最通用的形式中,傅里叶方法将由函数f确定的信号表示为所有可能频率的波的组合。这称为波的傅里叶变换。原始信号被替换成了它的频谱——一系列正弦和余弦分量的振幅和频率,相当于以另一种方式对同一信息进行了编码。工程师会谈论从时域到频域的转换。当以不同方式表示数据时,在一种表示中难以进行或不可能的操作可能在另一种表示中变得很容易。例如,你可以取一次电话交谈,对它做傅里叶变换,并去除信号中所有频率太高或太低导致人耳无法听到的傅里叶分量。这使得同样的信道可以发送更多的对话,这也是如今的电话费相对来说如此低廉的一个原因。你无法在未转换的原始信号上搞这一套,因为它没有“频率”这样一个明显的特征。你不知道该去掉什么。
在最近一次去柬埔寨的旅行中,我使用数码相机拍摄了大约1400张照片,全都塞进了一张2 GB的存储卡,还有空间可以再装400多张照片。确实,我拍的照片分辨率不是特别高,所以每个照片文件的质量大约是1.1 MB。但是图片是全彩色的,在27英寸的计算机屏幕上看不出任何明显的颗粒感,因此质量的损失并不明显。我的相机用了某种办法把十倍于这张2 GB存储卡容量的数据塞进了卡里,这就像把一升牛奶倒进一个蛋杯里。然而它还装下了。问题是:怎么装进去的呢?
答案是数据压缩。描述图像的信息经过处理来减小它的体积。这些处理中有一些是“无损”的,这意味着如果必要的话,可以从压缩的版本中恢复出原始信息。之所以能够做到这一点,是因为真实世界的大多数图像包含冗余信息。例如,大片的天空往往是相同的蓝色(这也是我们喜欢的地方)。你可以存储矩形的两个对角坐标,以及“将整个区域设为蓝色”的短代码,而不是一次又一次地重复蓝色像素的颜色和亮度信息。当然,实际的做法并不完全是这样,但它说明了为什么有时能够进行无损压缩。如果不是无损的,“有损”压缩也通常可以接受。人眼对图像的某些特征并不特别敏感,这些特征可以记录在较粗糙的尺度上,而我们大多数人不会注意到,特别是没有原始图像可供比较的时候。以这种方式压缩信息就像是打鸡蛋:在一个方向上很容易,也完成了所需的工作,但它是不可逆的。非冗余信息丢失了。只是考虑到人类视觉的工作原理,这些信息一开始就没起太大作用罢了。
与大多数随拍相机一样,我的相机将图片保存在带有类似于“P1020339.JPG”的标签的文件中。后缀指的是“联合图像专家组”(JPEG,joint photographic experts group),表明已使用特定的数据压缩系统。用于调整和打印照片的软件(例如Photoshop或iPhoto)都可以解码JPEG格式,并将数据再转换成图片。数以百万计的人经常使用JPEG文件,但知道它们被压缩了的人就不那么多了,而想知道工作原理的人就更少了。这并不是批评:你不必知道原理就可以使用它,这才是重点。相机和软件可以为你处理一切。但是,大致了解软件的作用以及原理往往是个好主意,哪怕只是为了了解有些软件是多么巧妙。如果你想的话,这里的细节可以跳过:我想让你体会一下相机存储卡中的每一张图片里融入了多少数学,但具体是哪些数学就不那么重要了。
JPEG格式融合了五个不同的压缩步骤。
第一步将颜色和亮度信息(开始时是红色、绿色和蓝色的强度)转换为另外三个在数学上等效,却更适合人类大脑感知图像的方式的信息。一个(亮度)代表整体亮度——同一图片的黑白或“灰度”版本。另外两个(色度)分别是亮度与蓝光量和红光量之差。
接下来,色度数据被粗粒化:压缩到更小的数值范围。仅这一步就可将数据量减半。它没有造成可感知的损失,因为人类视觉系统对色差的敏感度远低于相机。
第三步使用了傅里叶变换的一种变体。这不是用于随时间变化的信号,而是用于二维空间中的图案。数学基本上是一样的。所涉及的空间是图片中的8×8子像素块。为简单起见,只考虑亮度分量:同样的想法也适用于颜色信息。我们从一个64像素的块开始,对于每一个像素,我们需要存储一个数字,即该像素的亮度值。离散余弦变换是傅里叶变换的一种特殊情况,它将图像分解为标准“条纹”图像的叠加。其中一半图像的条纹是水平的,另一半是垂直的。条纹有不同的间隔,就像普通傅里叶变换中的各种谐波一样,其灰度值与余弦曲线非常接近。在块的坐标下,它们是各种整数m和n的cosmxcosny的离散版本,如图所示。
这一步为第四步铺平了道路,而第四步再次利用了人类视觉的不足。我们对大区域的亮度(或颜色)变化比对排列紧密的变化更敏感。因此,随着条纹的间距变得更精细,图中的图案就可以不用记录得那么精确。这进一步压缩了数据。
第五步,也是最后一步,使用“霍夫曼编码”来以更高效的方式表达64种基本图案的强度列表。
批注:感觉主要还是运用吧(捂脸)。
小波
由于这些应用,傅里叶分析已成为工程师和科学家的本能反应,但对于某些用途,该技术有一个重大缺陷:正弦和余弦会延伸到无穷。傅里叶的方法在试图表示短信号时会遇到问题。它需要大量的正弦和余弦才能模仿局部的尖峰。问题不在于把尖峰的基本形状搞对,而是要让尖峰之外的所有东西都等于零。你必须砍掉所有那些正弦和余弦无限长的波动尾巴,做法是添加更多的高频正弦和余弦来拼命抵消不必要的垃圾。因此傅里叶变换对于类似尖峰的信号是非常糟糕的:变换后的版本比原始版本更复杂,需要更多数据来描述它。
挽救局面的是傅里叶方法的一般性。正弦和余弦可以用在这里,因为它们满足一个简单条件:它们在数学上是独立的。正式来说,这意味着它们是正交的:在一种抽象但容易理解的意义上,它们彼此成直角。欧拉的技巧(最终由傅里叶重新发现)就在这里派上了用场。将两个基本正弦波形相乘并在一个周期内积分,就可以衡量它们之间的关系是否密切。如果积分结果很大,说明它们非常相似;如果积分结果是零(正交性的条件),说明它们相互独立。傅里叶分析之所以成立,是因为它的那些基本波形既正交又完备:它们是独立的,而且有足够多种,适当地叠加后足以表达任何信号。实际上,它们相当于所有信号构成的空间上的一个坐标系,就像普通空间中的三个轴一样。主要的新性质是我们现在拥有无限多个轴:每个基本波形都是一个轴。一旦你适应了这种思想,它就不会在数学上造成多少困难。它只是意味着,你必须使用无穷级数而不是有限和,并且稍微留意一下级数什么时候收敛。
即使在有限维空间中,也存在许多不同的坐标系。例如,旋转轴可以指向新方向。所以在信号的无限维空间中,存在与傅里叶非常不同的另外一些坐标系也就不足为奇了。近年来,整个领域中最重要的发现之一就是一种新的坐标系,其基本波形被限制在有限的空间区域里。它们被称为“小波”,可以非常有效地表达尖峰,因为它们本身就是尖峰。
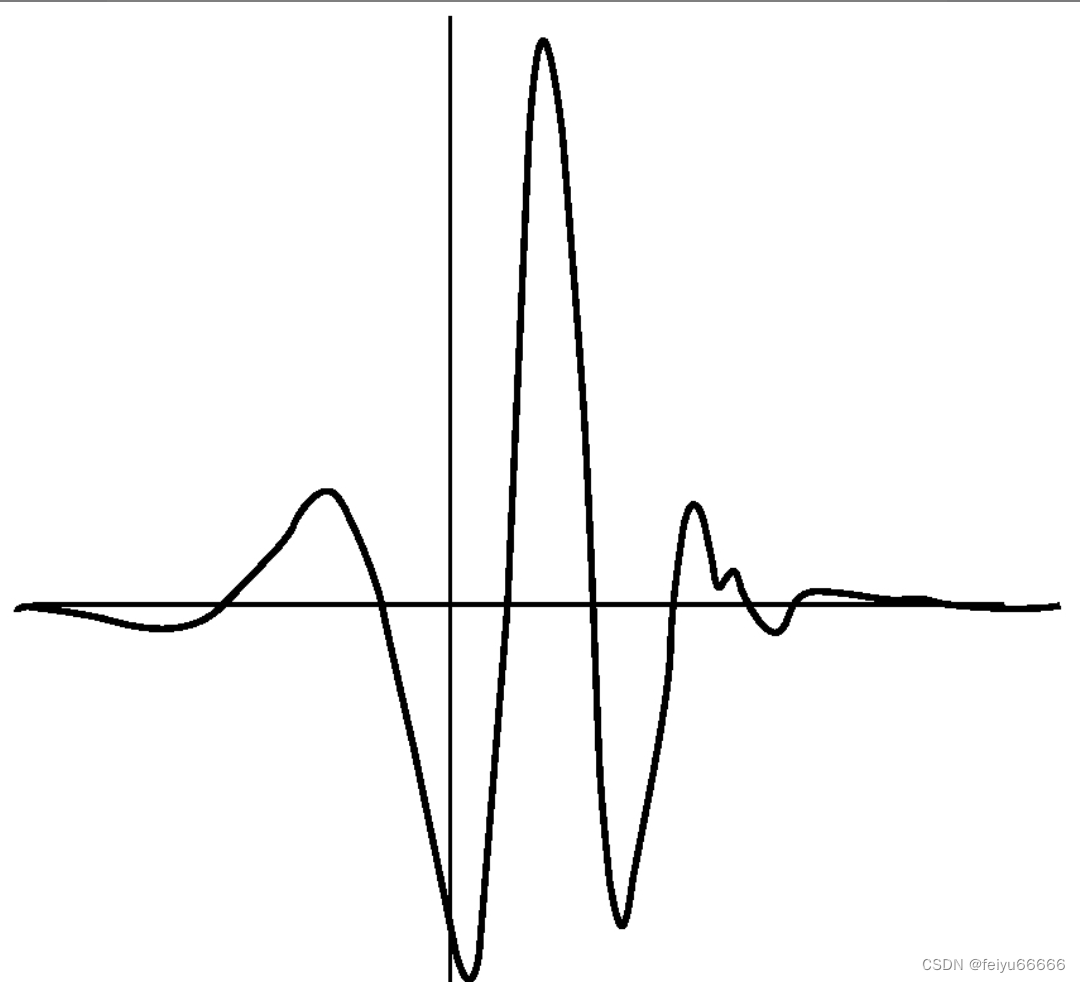
直到最近才有人意识到,可以进行类似尖峰的傅里叶分析。起步很简单:选择特定形状的尖峰,即“母小波”。然后将母小波侧向滑动到各个位置,并改变比例来扩展或压缩,从而生成子小波(以及孙小波、曾孙小波,等等)。同样道理,傅里叶的基本正弦和余弦曲线是“母小正弦波”,而高频率的正弦和余弦曲线是“子小正弦波”。不过这些曲线是周期性的,和尖峰看起来不一样。
小波被设计用于有效地描述类似尖峰的数据。此外,由于子小波和孙小波只是母小波的缩放版,因此可以聚焦于特定的细节水平。如果你不想看到细微的结构,只需从小波变换中删除所有的曾孙小波就好了。要用小波表达豹子,你需要用几个大的小波表示豹子的身体,用较小的小波表示眼睛、鼻子,当然还有斑点,用非常小的小波来表示一根根毛发。要压缩表达豹子的数据,你可能会认为单根毛发无关紧要,因此只需删除这些特定的小波分量。最棒的是,图像仍然看起来像豹子,它仍然有斑点。如果你尝试使用豹子的傅里叶变换进行这个操作,那么分量列表会很长,你也不清楚应删除哪些项,结果可能认不出来那是只豹子了。
这一切都非常好,但母小波应该是什么形状呢?在很长一段时间里,没有人可以解决这个问题,甚至也没法证明这样好的形状存在。但在20世纪80年代初,地球物理学家让·莫莱(Jean Morlet)和数学物理学家亚历山大·格罗斯曼(Alexander Grossmann)发现了第一个合适的母小波。1985年,伊夫·梅耶尔(Yves Meyer)发现了一个更好的母小波。1987年,贝尔实验室的数学家英格丽·多贝西(Ingrid Daubechies)彻底颠覆了整个领域。虽然之前的母小波看起来很像尖峰,但它们都有一个非常微小的数学尾巴,一直摆动到无限远。多贝西发现了一个没有尾巴的母小波:在某个时间间隔之外,母小波总是恰好为零——这是一个真正的尖峰,完全局限于一个有限的空间区域内。
小波类似于尖峰的特征使它们特别适合压缩图像。它们最初的大规模实际用途之一是存储指纹,客户是美国联邦调查局(FBI)。FBI的指纹数据库包含3亿条记录,每条记录有8个指纹和2个拇指纹,最初存储在纸卡上。这种存储介质使用不便,于是他们把图像数字化并将结果存储在计算机上。明显的优势包括能够快速自动搜索与犯罪现场发现的指纹相匹配的指纹。每张指纹卡的计算机文件长度为10兆字节(MB):8000万位二进制数字。因此整个存档占用3000TB的存储空间:2.4亿亿个二进制数字。更糟糕的是,每天要增加3万个新指纹。因此存储需求每天将增加2.4万亿位二进制数字。FBI明智地判断自己需要一些数据压缩方法。由于各种原因,JPEG不适合,因此在2002年,FBI决定使用小波,即“小波/标量量化(WSQ)方法”来开发一种新的压缩系统。WSQ通过删除整个图像中的细节,将数据减少到其大小的5%。这丝毫不影响眼睛或计算机识别指纹的能力。
小波最近还有许多在医学成像方面的应用。医院现在使用几种不同类型的扫描仪来获得人体或重要器官(如大脑)的二维横截面。这些技术包括CT(计算机断层扫描术)、PET(正电子发射体层成像)和MRI(磁共振成像)。在断层扫描术中,机器在身体的单一方向上观察总组织密度或类似的量,就像你在固定位置看看所有组织是不是会变得稍微透明一样。通过从许多不同角度拍摄一系列这样的“投影”,再用上一些巧妙的数学,就可以重建二维图像。在CT中,每个投影都需要X射线暴露,因此有充分的理由来限制所获取的数据量。一方面,在所有这些扫描方法中,较少的数据在获取时所需的时间也较少,同样的设备就可以用于更多的患者。另一方面,良好的图像需要更多的数据,才能让这种重建方法工作得更好。小波提供了一种折中方案,减少的数据量也带来同样可接受的图像。通过小波变换去除不需要的分量,再次“反变换”得到图像,就可以平滑和清理不良的图像。小波还从根本上改进了扫描仪获取数据的方式。
事实上,小波几乎到处都是。地球物理学和电气工程领域虽然相隔遥远,研究人员却都在把小波引入自己的领域。罗纳德·考夫曼(Ronald Coifman)和维克多·魏克尔豪斯(Victor Wickerhauser)用它们来消除录音中不想要的噪声:最近的一次成功是一场演出——勃拉姆斯演奏他自己的《匈牙利舞曲》。录音最初于1889年记录在蜡筒上,而蜡筒已经部分熔化;之后它被重新录制到78转的唱片上。考夫曼从唱片的一次无线电广播入手,当时音乐几乎已经完全湮没在周围的噪声里。在利用小波进行“清洗”之后,你就可以听到勃拉姆斯的演奏了——并不完美,但至少听得见。对于一个200年前首次在热流物理学中出现,并被拒绝发表的想法来说,这样的战绩可谓辉煌。