一、主要参考:
C/C++编程笔记:C语言对齐问题【结构体、栈内存以及位域对齐】_二进制异常退出,栈对齐-CSDN博客
其中关于内存对齐,讲了结构体以及位域,以及一些容易出错的地方,非常好。
结构体对齐:


下面提到的对齐模数就是上面提到的有效对齐值N。
位域对齐:

注意,这里讲位域只能用在结构体或联合体中。


注意位域对齐,既要考虑自身字节存储时需不需要填充位,又要考虑整体作为结构体存储时需不需要填充字节。
注意事项:


![]()

写的很好了。
二、
结构体对齐规则整理,可以看这篇:
C语言结构体对齐详解-CSDN博客
有个规则总结:注意结构体各成员变量字节数先取最大值,然后和系统设定对齐字节数,取较小值,作为最终结构体对齐字节数,即结构体总字节数需要是这个字节数的整数倍。
参考以下程序,也是网上公开的:
//内存对齐计算验证实例
#include<stdio.h>
#include <stddef.h>#pragma pack(2) // 值只能填1 2 4 8 16 但是当#pragma pack指定的值等于或者超过所有数据成员长度的时候,这个指定值的大小将不产生任何效果typedef struct test {char a;int b;double c;char d;
}Test;int main(int argc, char** argv)
{Test T;int offset_a = offsetof(Test, a);int offset_b = offsetof(Test, b);int offset_c = offsetof(Test, c);int offset_d = offsetof(Test, d);printf("The length of char type is %u\n", sizeof(char));printf("The length of int type is %u\n", sizeof(int));printf("The length of double type is %u\n\n", sizeof(double));printf("The length of the whole struct is %u\n\n", sizeof(T));printf("The offset of first data member is %d\n", offset_a);printf("The offset of second data member is %d\n", offset_b);printf("The offset of third data member is %d\n", offset_c);printf("The offset of fourth data member is %d\n\n", offset_d);printf("The begin address of first data member of struct test is %p\n", &(T.a));printf("The begin address of second data member of struct test is %p\n", &(T.b));printf("The begin address of third data member of struct test is %p\n", &(T.c));printf("The begin address of fourth data member of struct test is %p\n\n", &(T.d));return 0;
}这个结果是16。很容易错。
因为一般不加#pragma pack(2)这句,则系统默认是8字节对齐,刚好结构体中double型变量字节数是8,则最终结构体存储需要8字节对齐,即总字节数需要是8的整数倍,算出结果是24。即:1+3(填充)+4+8+1+7(填充)。
如果将#pragma pack(2)中2改为1,即,1字节对齐,则实际上不补充字节了。
三、
第一篇文章最后总结,栈的对齐问题:

栈的内存对齐问题,可能不对。可参看下面文章:
内存对齐:C/C++编程中的重要性和技巧_malloc 内存对齐-CSDN博客
但是这篇写的比较啰嗦,关注的栈内存对齐和结构体对齐的区别在这:
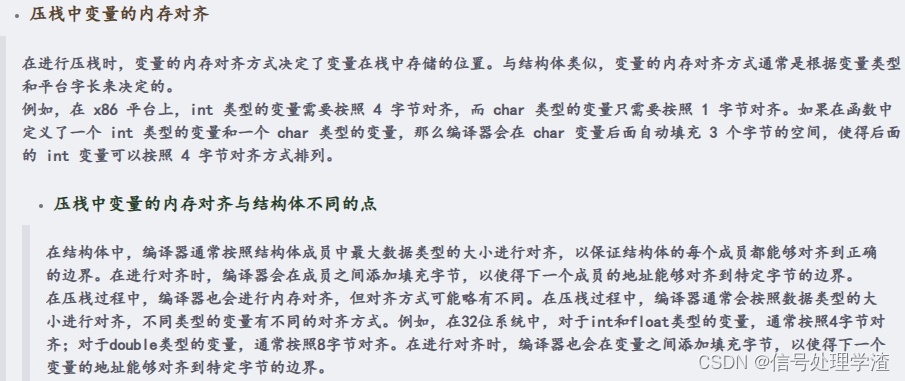
即,结构体作为一个整体,整个结构体变量需要在考虑每个成员变量按照各自数据类型在内存中对齐存储之外,最终可能还需要额外在尾部补充字节使结构体总字节数是其字节数最长的成员变量对应的数据类型字节数和系统对齐设置字节数中较小者的整数倍(参考结构体对齐字节数规定哈)。而栈对齐,只考虑每个变量按各自数据类型对齐地址存储即可。



![[开源]EBO机器人改装 动力增强板 最简单的4G无线距离小车](https://img-blog.csdnimg.cn/direct/4fff406d3aa541a48ed903d2096b9352.png)