- 39. 组合总和

// 剪枝优化 class Solution {public List<List<Integer>> combinationSum(int[] candidates, int target) {List<List<Integer>> res = new ArrayList<>();Arrays.sort(candidates); // 先进行排序backtracking(res, new ArrayList<>(), candidates, target, 0, 0);return res;}public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {// 找到了数字和为 target 的组合if (sum == target) {res.add(new ArrayList<>(path));return;}for (int i = idx; i < candidates.length; i++) {// 如果 sum + candidates[i] > target 就终止遍历if (sum + candidates[i] > target) break;path.add(candidates[i]);backtracking(res, path, candidates, target, sum + candidates[i], i);path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素}} }思路:典型的回溯算法,套用回溯三部曲就可以,这道题可以在for循环里面做剪枝操作,if(sum + candidates[i])>target 就终止遍历
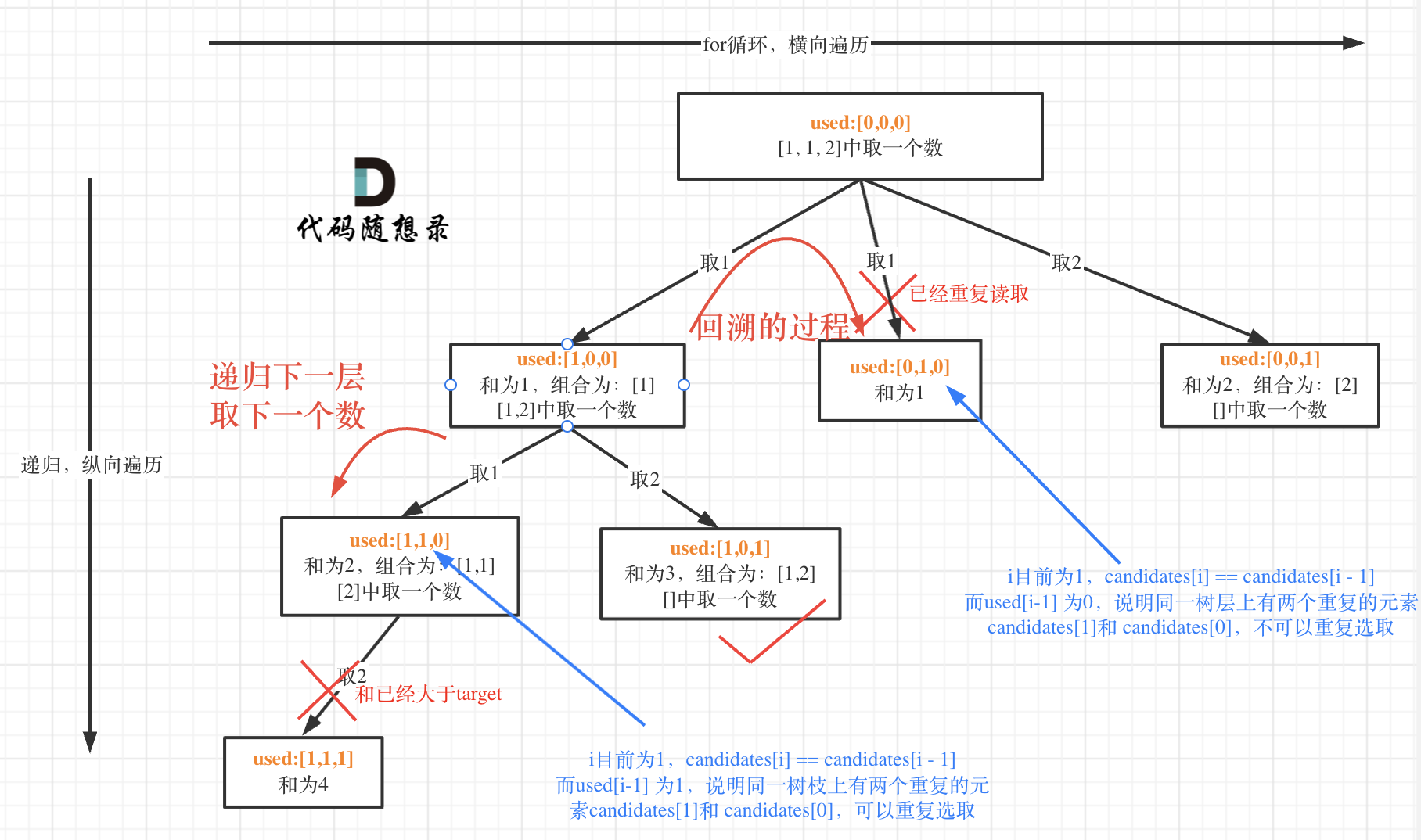
- 40.组合总和II

class Solution {LinkedList<Integer> path = new LinkedList<>();List<List<Integer>> ans = new ArrayList<>();boolean[] used;int sum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {used = new boolean[candidates.length];// 加标志数组,用来辅助判断同层节点是否已经遍历Arrays.fill(used, false);// 为了将重复的数字都放到一起,所以先进行排序Arrays.sort(candidates);backTracking(candidates, target, 0);return ans;}private void backTracking(int[] candidates, int target, int startIndex) {if (sum == target) {ans.add(new ArrayList(path));}for (int i = startIndex; i < candidates.length; i++) {if (sum + candidates[i] > target) {break;}// 出现重复节点,同层的第一个节点已经被访问过,所以直接跳过if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {continue;}used[i] = true;sum += candidates[i];path.add(candidates[i]);// 每个节点仅能选择一次,所以从下一位开始backTracking(candidates, target, i + 1);used[i] = false;sum -= candidates[i];path.removeLast();}} }思路:回溯思路与上题差不多,主要是去重的操作,去重分为树枝去重和树层去重,本题是树层去重,同一层的数据,与前一个数据相等时,去重(跳过),用used[i-1]==false保证是同一层的而不是同一个树枝。
-
- 131.分割回文串

class Solution {List<List<String>>result = new ArrayList<>();LinkedList<String>path = new LinkedList<>();public List<List<String>> partition(String s) {backTracking(s, 0);return result;}public void backTracking(String s, int startIndex){if(startIndex == s.length()){result.add(new ArrayList<>(path));}for(int i = startIndex ; i < s.length() ; i++){if(isPalindrome(s, startIndex, i) == true){path.add(s.substring(startIndex, i+1));}else{continue;}backTracking(s, i+1);path.removeLast();}}public boolean isPalindrome(String s, int startIndex, int endIndex){for(int i = startIndex, j = endIndex ; i < j ; i++, j--){if(s.charAt(i) != s.charAt(j)){return false;}}return true;} }思路:该题和组合问题类似,主要是要理清startIndex代表分割位置的思想,相当于画线操作,当一个区间为回文串的时候,add进path中,回溯终点是startIndex==s.length()
代码随想录算法训练营29期|day27 任务以及具体安排
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/422189.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
数字湖南劲风起:纷享销客当选2023年湖南省数字化十大优秀服务商
1月19日,湖南省数字经济促进会主办的长江数字经济发展大会暨第四届湖南省数字经济论坛圆满举行,纷享销客凭借过硬的产品实力、优质的服务水平及行业口碑,当选【2023年湖南省数字化十大优秀服务商】! “一江一体同风起,…
flutter 实现定时滚动的公告栏的两种不错方式
相同的部分
自定义一个类继承StatefulWidget
所有公告信息存放在list里
第一种 scrollControllerAnimatedContainer
逻辑如下 我们可以发现启动了一个timer计时器计时5秒,hasClients检查其目标对象(我们用的是listview)是否被渲染&#x…
捆扎机怎么调整松紧度
捆扎机松紧力度可以通过以下方法调节: 1. 调节束紧力:捆扎机上通常有专门的调节束紧力的旋钮。顺时针方向转动螺帽,对弹簧的压力就会减小,打包机就会越松;逆时针调整,打包机就会越紧。正常情况下࿰…
Uni-App三甲医院、医保定点三甲医院在线预约挂号系统源码
医院在线预约挂号系统是一种方便患者预约挂号的系统,患者可以通过该系统进行预约挂号,省去了到医院现场排队等待的时间,提高了就诊效率。随着医院信息化水平的不断发展,医院在线预约挂号管理系统已成为医院管理中不可或缺的一部分…
人大金仓数据库授权文件过期解决
一台用于测试的人大金仓数据库访问失败。
登录后发现服务停了。
使用命令行启动,提示服务过期。 查网上资料,说替换原有文件可以解决。
于是去官网下载一个新的,替换掉原来的授权文件。
再次启动数据库,还是提示授权文件过期。…
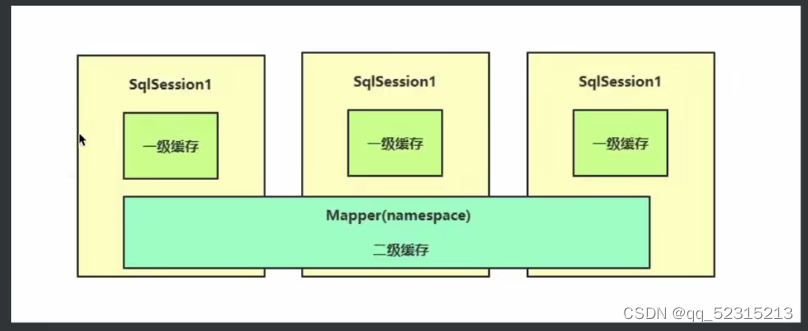
mybatis的缓存机制
视频教程_免费高速下载|百度网盘-分享无限制 (baidu.com)
MyBatis 有一套灵活而强大的缓存机制,主要分为两级缓存:一级缓存(本地缓存)和二级缓存(全局缓存)。 一级缓存(本地缓存)&a…
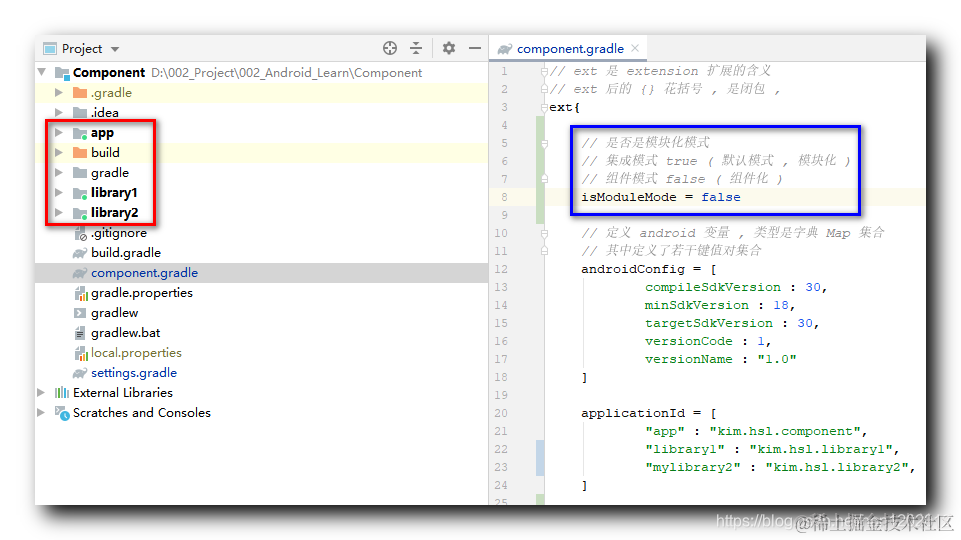
Android学习之路(22) 从模块化到组件化
从模块化到组件化
一、从模块化到组件化
Android 应用项目 , 都存在一个应用模块 ( Application Module ) , 在 build.gradle 构建脚本中 , 第一个插件配置 com.android.application , 表明 该 Module 编译打包后的输出是 APK 安装包 ; 该项目可以直接运行 ;
plugins {id co…
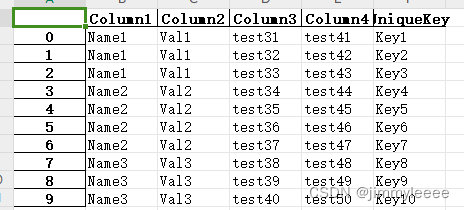
用pandas实现用前一行的excel的值填充后一行
今天接到一份数据需要分析,数据在一个excel文件里,内容大概形式如下: 后面空的格子里的值就是默认是前面的非空的值,由于数据分析的需要需要对重复的数据进行去重,去重就需要把控的cell的值补上,然后根据几…
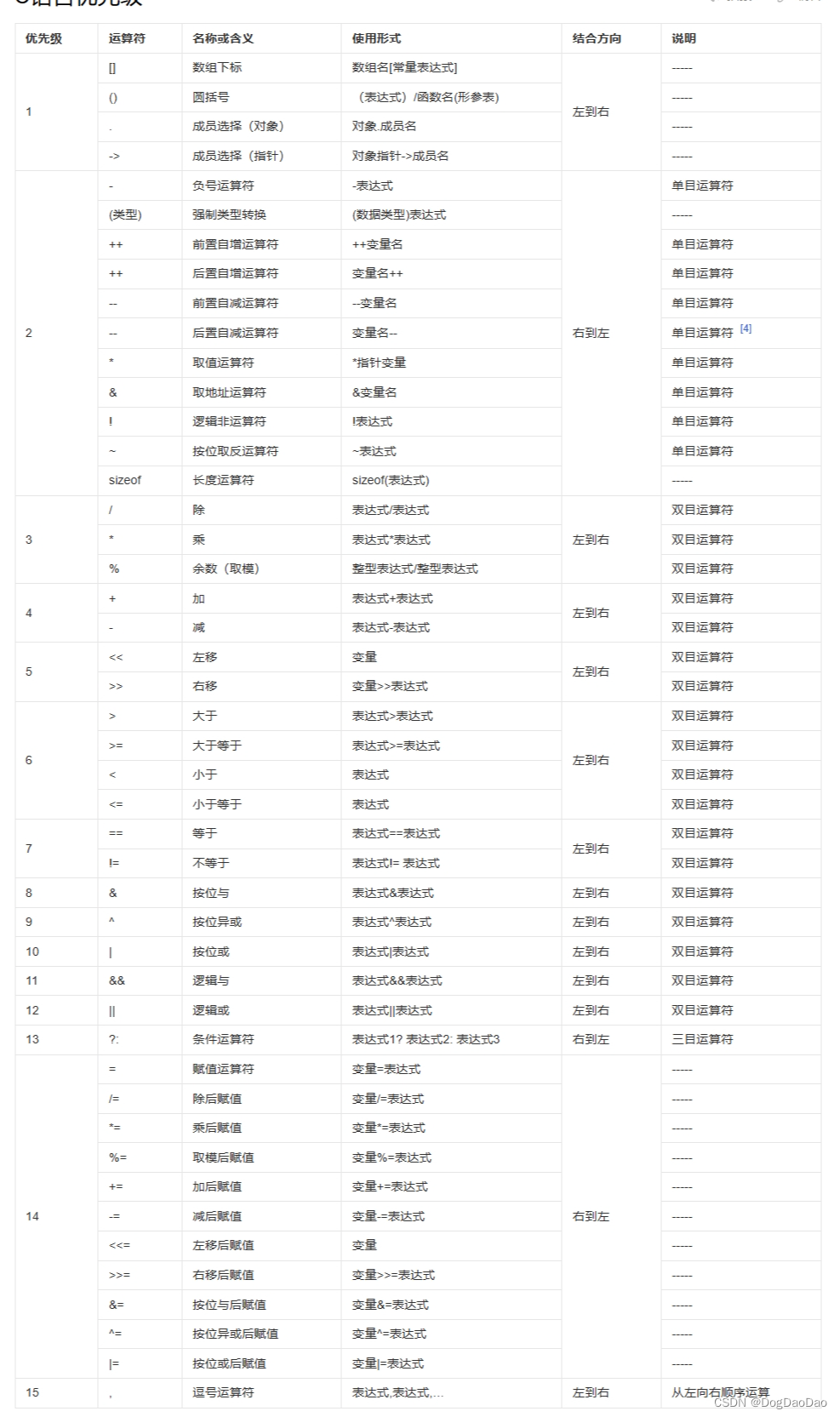
c/c++的指针函数与函数指针
函数
定义: 函数是数学中的一个概念,它是定义在某个数集上的一个特殊的映射关系。函数将输入值(或自变量)映射到输出值(或因变量)。函数的输入和输出可以是任何类型的数据,如数字、字符串、数组…
中霖教育:注册会计师与中级会计师有什么区别?
在财会行业,注册会计师与中级会计师是两种不同的职业证书,二者之间有很大的区别,都有很高的含金量,考生们可以根据自身情况进行选择,
1.证书性质不同
注册会计师属于基本资格,如果没有注会证书是不能从事…
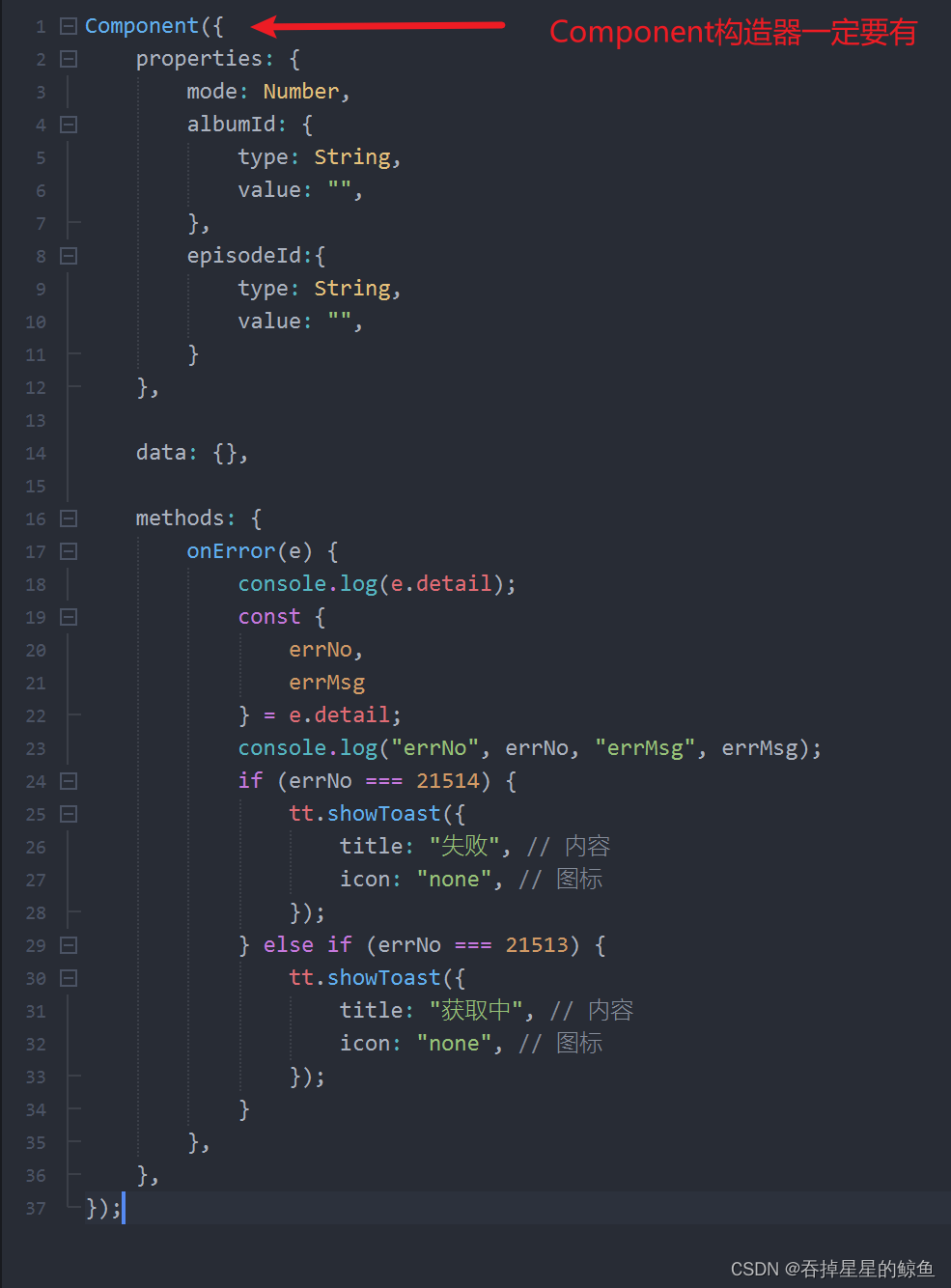
uniapp使用自定义组件
tt.vue中使用video-player组件
用到的目录如下: pages.json {"path": "pages/Tabbar/tt/tt","style": {"navigationBarTitleText": "","enablePullDownRefresh": false,// 使用自定义组件"using…
B-Tree详解及编码实现
一、概念和特性 1、定义 B-Tree是一种平衡的多叉树,适用于外查找多路搜索树,这种数据结构能够保证数据节点查找、顺序访问、插入、删除的动作,其平均时间复杂读控制在O(logN)内;B树为系统大块数据的读写操作做了优化,少定位记录时…