实时渲染 -- 光栅化（Rasterization）-编程知识

图元（Primitive）

在进行渲染之前，我们需要输入装配图元数据，因此需要先定义图元结构，一般有：三角形、四边形、多边形、线段、点

最常用的图元就是三角形了，选择它的理由有很多：

三角形是最基础的几何面，可以组成任意边形
在三维空间中，3个顶点组成的面一定是三角形，但4个顶点组成的面不一定是四边形（例如一张纸沿对角线折叠）
三角形一定是凸多边形（凹多边形很容易导致算法错误或者更复杂的算法实现）
三角形可使用易于实现的三角插值

三角形遍历（Triangle Traversal）

有了图元数据后，经过MVP变换和视口变换（Viewport Transform）后会得到屏幕空间上的顶点数据（三角形顶点无论如何变换最后顶点组成的形状仍然为三角形），而接下来就需要使用光栅化去将这种顶点数据生成用于显示的像素数组。

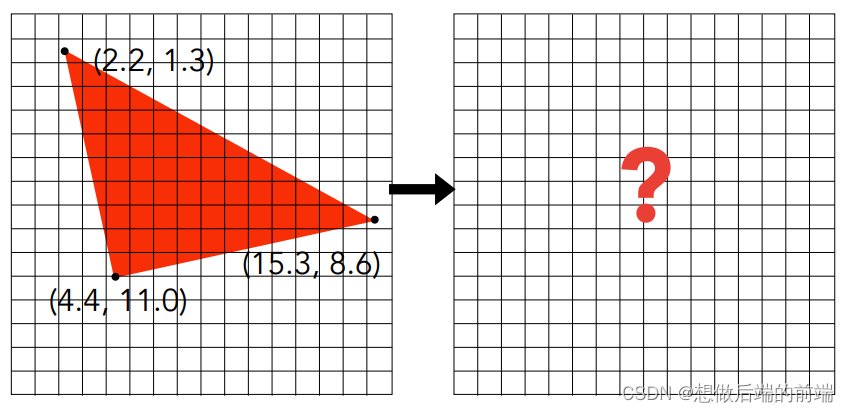
基于屏幕像素的采样

一个最简单的想法就是将屏幕像素进行遍历，测试其每个像素是否在三角形内部。可以预见的是，这种光栅化方式必然带来极高的时间复杂度

for (int x = 0; x < width; ++x)
for (int y = 0; y < height; ++y)image[x][y] = inside(Vector2(x+0.5,y+0.5),tri);//判断点在三角形内部，若在内部则返还1，若在外部则返还0
int inside(Vector2 p,Vector2 vertexs[3]){for(int i = 0; i < 3; ++i){//假设三角形的边edge都是逆时针方向Vector2 edge = vertex[(i+1)%3]-vertex[i];Vector2 vec = vertex[i] - p;int result = cross(edge,vec);//若点在三角形内，得到的叉积值应均为正数if(sign(result) == 0) return 0;//注：无背面剔除时，得到叉积值均为正数或者均为负数时都应返还true}return 1;
}

基于包围盒的采样

一个更好的方法是，用包围盒对三角形进行包围（可使用AABB盒），然后无需对整个屏幕的像素进行循环遍历，而只需对包围盒范围内的像素进行循环遍历：

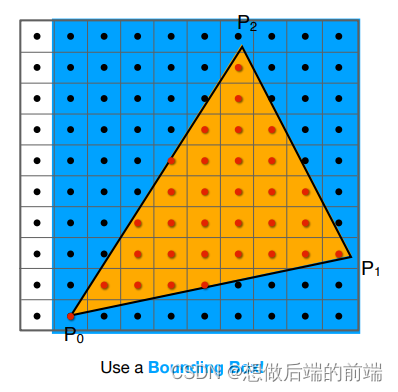
基于自增的采样

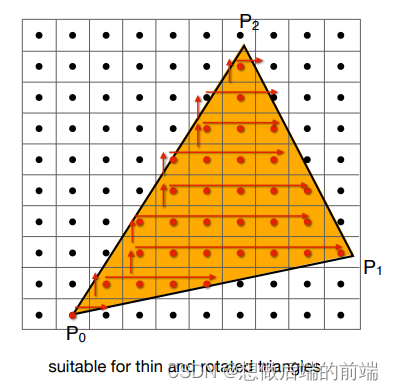
还有一个做法：

从最下边的一行（顶点的最小y值）开始，找到最左边的格子（顶点的最小x值）作为起点
从左往右遍历，一旦遇到0就停止遍历。
回到起点，然后往上一行，开始从左往右寻找新起点，一旦遇到1（意味着找到新起点了）就停止遍历
找到新起点后重复步骤2和3，直到找不到新起点（这意味着步骤3最终遍历到了顶点最大x值）

虽然循环次数少了（可能适用于狭长的三角面），但由于实现复杂，且不容易实现并行化计算（每一行每一列都有依赖关系），因此实际效率并不会快多少。

抗锯齿（Anti-Aliasing）

信号与采样

光栅化的采样会遇到一些走样（Aliasing）问题：锯齿现象、摩尔纹。

锯齿：光栅化不可避免的问题就是会产生锯齿，其原因在于屏幕像素的采样是离散的，不可能精确表示三角形。

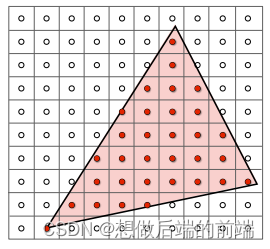
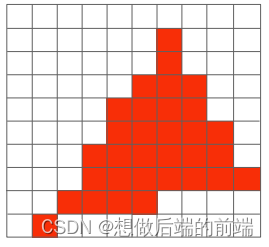
摩尔纹：摩尔纹是采样时可能会出现的另一种不理想的怪异现象。

解释走样问题之前，首先我们来认识一下信号：信号本质上就是一个函数，输入参数，输出结果。对于任何函数f(x)，都有两种表现形式：时域、频域。其中我们最常见的便是时域的形式，也是现实世界的直观形式，可以理解成即f(x)本身，把x当成时间，那么时域便是分析函数值关于时间x的关系。

而傅里叶告诉我们，任意一个函数 f(x)可以由若干个频率不同、振幅不同的余弦函数相加而成。

当我们每隔一定间隔采样 f(x)，实际上就是每隔一定间隔，分别采样这些组成信号的余弦波并相加起来。下图可以看到，低频余弦波的采样结果与实际余弦函数差别并不大，但是随着频率越来越高，余弦波的采样失真越来越严重了。

尤其最下面的高频余弦波，本该是剧烈起伏的，采样的结果却是平缓起伏，与实际结果已经严重不一致

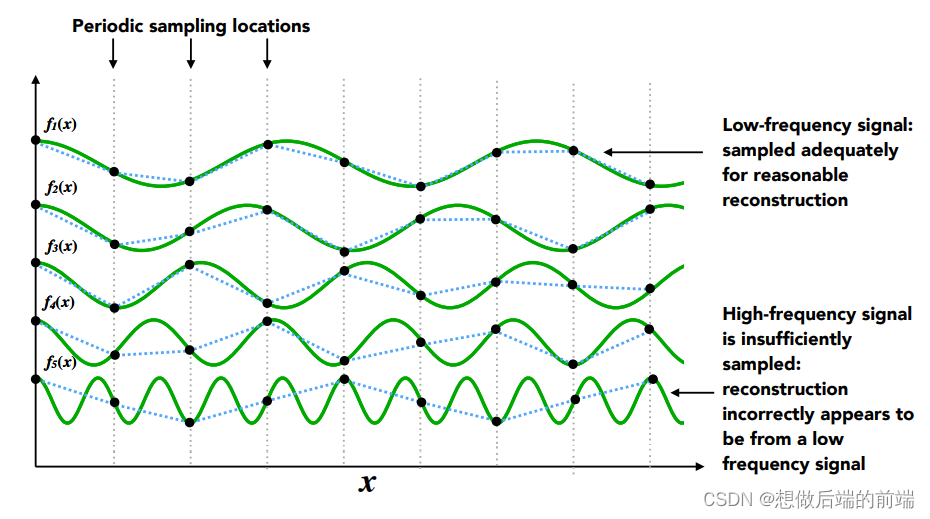
因此，我们可以得出结论：当采样频率过低（采样间隔过大）时，信号中的高频信息会失真，这也是走样问题的来源。反走样要做的就是尽可能让高频信息量减少（高频余弦波的振幅减少）。

那么，对于目标采样频率（目标分辨率）的反走样基本原理为：

先把原始图片当成一种信号，即信号 f(x)输入一个二维位置x，输出一个像素颜色值（那么自然而然，这张图片也可以由若干个不同频率的余弦波组成）
接下来，我们对时域函数（图片信号）进行卷积操作（即模糊图片），卷积操作实际上就是每个点取周围（包括点本身）的平均值。

容易想象得出到，经过卷积后的时域函数 f(x) 会变得更加平缓（图片变得更加模糊）。这样分离出来的高频余弦波振幅更加小，换句话说，相当于我们把高频信息剁掉了。

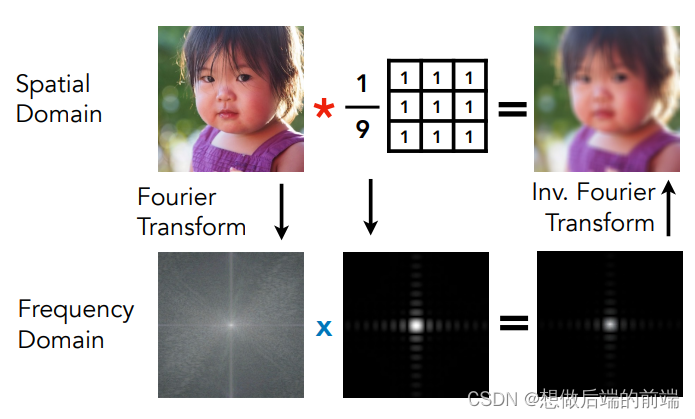
3. 最后，我们对这张卷积后的图片进行目标频率的采样，就能得到走样现象不明显的目标分辨率图片。

SSAA（超采样抗锯齿）

SSAA（Super Sampling Anti-Aliasing 超采样抗锯齿）：先进行高频率的采样并着色到高分辨率的buffer上，然后目标分辨率下的每个目标像素颜色会综合混合高分辨率buffer中对应的多个像素颜色去生成目标画面。（相当于，先进行高频率采样，接着进行卷积操作，最后再进行目标频率采样得到目标分辨率图片）

例如，在4xSSAA算法中，假设最终屏幕输出的分辨率是800x600, 4x SSAA就会先光栅化到一个分辨率1600x1200的buffer上并逐个像素着色，然后再直接把这个放大4倍的buffer下采样至800x600的画面

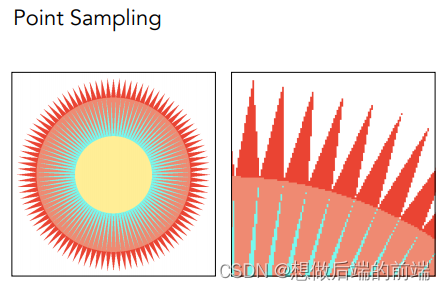
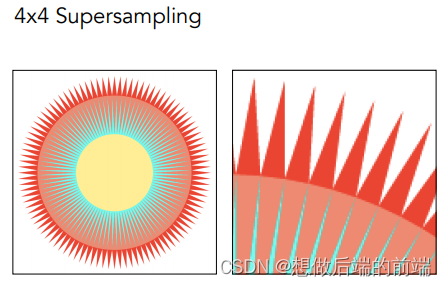
SSAA 是一种最原始的抗锯齿方法，虽然得到的图片锯齿感少了很多，代价是：例如4x SSAA，光栅化和着色的计算负荷都比原来多了4倍，buffer存储空间的大小也比目标分辨率多了4倍。

MSAA（多重采样抗锯齿）

MSAA（MultiSampling Anti-Aliasing 多重采样抗锯齿） 也是一种超采样的抗锯齿方法，但是做法更加聪明：光栅化只在采样时采样更多点，最后根据每个像素格子采样结果的覆盖率来填入像素格子。（相当于，先进行卷积操作，最后再进行目标频率采样得到目标分辨率图片）

实际应用的话，采样点位置不一定是标准细分正方形的中心位置，也可以是不规则分布的位置。

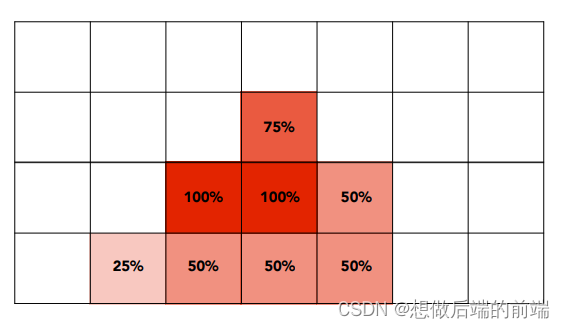
可以看到，4x MSAA在光栅化计算负荷比原来多了4倍，但是到了像素着色（pixel shading）阶段的时候，每个目标像素只着色1次（4x SSAA对应一个目标像素则需要计算4个高分辨率像素，即4次着色），而且也不需要更大的buffer存储（4x SSAA需要4倍的buffer存储）

MSAA的一个问题就是和延迟渲染（Deferred Shading）框架并不是那么兼容。因为用延迟渲染的时候场景都先被光栅化到GBuffer上去了，不直接做着色。

FXAA（快速近似抗锯齿）

FXAA（Fast Approximate Anti-Aliasing 快速近似抗锯齿） 是一种图像后处理技术。它先直接采样得到目标图像，然后通过像素颜色检测边缘。这种方法使得颜色变化剧烈的像素会被认为是边缘，精度可能不好，但是处理速度非常快。

它不属于先前的信号反走样思路，而是属于一种让画面看上去更舒服的trick。

后处理技术的抗锯齿方法一般没倍数概念，这是因为图像不存在放大。

TAA（帧间抗锯齿）

TAA（Temporal Anti-Aliasing 帧间抗锯齿） 是最常用的图像后处理技术。

TAA 的核心思想是将采样点从单帧分布到多个帧上（从时间的维度上去采样），即对上一帧图像对应的位置进行采样，得到的像素以一定比例混入当前帧的图像像素中，这样当连续的多个帧的数据混合起来以后，就相当于对每个像素进行了多次采样。

采样时还需要进行抖动操作（即每帧采样的位置有一定随机偏移），这是避免画面静止时导致重复对相同的位置采样从而导致整个图像相当于采样次数没有增加，造成抗锯齿失效。

其中，TAA 使用了运动矢量（motion vector）来确定前一帧在何处进行采样，然后将与当前帧的像素进行混合。

所谓运动矢量，其实就是一个空间中的物体（更准确说是物体像素点）在上一帧的位置与下一帧的位置之差，这往往要借助G Buffer信息来找到，具体算法稍微复杂。

TAA 的缺点是，由于每一帧图像的像素颜色实际上是根据以前的帧来进行混合的，因此容易产生画面延迟感；而且当物体运动过快时，会出现物体的残影现象。

TXAA

TXAA 是后来NVIDIA提供的抗锯齿技术，实际上就是TAA+MSAA的组合。

通过引入额外的深度信息来支持在延迟渲染（Deferred Shading）上使用MSAA，TXAA综合了MSAA的强大能力与类似于CG电影中所采用的复杂的高画质过滤器。还可以抖动帧与帧之间的采样位置来获得更高画质。

DLSS（深度学习超采样）

DLSS（Deep Learning Super Sampling 深度学习超采样技术） 则是NVIDIA在Turing架构的时候推出的基于深度学习方法的图像后处理技术。

DLSS 1.0 的基本工作原理是：利用NVIDIA神经图形框架NGX，在超级计算机中以极低的帧率和每像素64个样本对数万张高分辨率的精美图像进行离线渲染，训练出一个深度神经网络。基于无数个小时的训练所获得的数据，网络就可以将分辨率较低的图像作为输入，输出一个高分辨率的精美图，并在一定程度上避免了出现 TAA 等传统方法的模糊、不清晰和透明问题。

DLSS 也不属于先前介绍的信号反走样思路，而是通过低分辨率画面去”猜测“出高分辨率画面，这种猜出来的信息已经不算是来源于正确的原始信号了。

DLSS 2.0 则额外依赖了G Buffer的信息（这点与TAA有一定相似），从而“猜测”更加有依据、精确，能够输出锯齿现象更加轻微、画面更加清晰的高分辨率画面。

可见性/遮挡（Visibility/Occlusion）

前面我们知道如何将一个三角形光栅化到屏幕上，而接下来的问题是当场景中有大量三角形时，我们还需要将它们光栅化的结果综合起来。

画家算法（Painter's Algorithm）

画家算法是最原始的算法，就是简单地将三角形进行排序，根据z值（离摄像机的前后距离）的顺序，将三角形逐个进行光栅化，并且当光栅化遇到冲突时（以前有三角形光栅化占据了这个像素）强制覆盖之。

画家算法的缺点：

以三角形的z距离进行排序，需要一定开销，时间复杂度为O(nlogn)�(��)，n为三角形个数
以三角形为单位可能会发生不准确的z值排序，如画家算法无法渲染出下图

深度测试（Z-Test）

Z-Test则是一种主流且被硬件支持的遮挡剔除技术，其原理是提供一个额外存储最小z值的buffer（经过变换后的坐标z值越小，实际上就是越接近摄像机），这样实际有两个buffer：

frame buffer：负责存储像素颜色，也就是存储图像用的
z-buffer(depth buffer)：负责存储深度值（z值）

Z-Test技术实际上就是：每次光栅化且像素着色（Pixel/Fragment Shader）后的每个像素z值先和z-buffer的对应像素深度进行比较，若更小（意味着离摄像机更近），则像素颜色写入frame buffer对应位置且z值覆盖写入z-buffer对应位置；若更大，则抛弃（discard）像素。

for (each triangle T)
for (each sample (x,y,z) in T){if (z < zbuffer[x,y]){      // closest sample so farframebuffer[x,y] = rgb; // update colorzbuffer[x,y] = z;       // update depth}else{;} // do nothing, this sample is occluded
}

总结Z-Test有如下特点：

Z-buffer的时间复杂度是O(n)，n为三角形个数
绝大部分GPU硬件都实现了Z-Test算法，可以较快执行

Early-Z

Z-Test的一个缺点是，当花费了较多的像素着色计算（Pixel/Fragment Shader 负责光照和纹理采样等大量计算）后得到的像素点有可能被抛弃，这就造成了计算性能的浪费。而 Early-Z 的原理就是把Z-Test的操作提前到光栅化之后和像素着色之前，这样就避免了本就该被抛弃的像素进行额外的像素着色计算。

有一些情况是不适用于Early-Z技术的：像素着色计算可能会修改z深度值、Alpha Test等。这时候用Early-Z技术是不准确的，必须老老实实用Z-test，即等到光栅化和着色后才决定是否抛弃像素。

然而Early-Z性能是不稳定的，最坏情况就是从远到近渲染每个三角形，这样对每个三角形的所有像素都要进行像素着色计算（代价和Z-test一样），而最好情况就是从近到远渲染，这样就不会出现overdraw。

Z-prepass 改进：使用额外一个pass（理解成跑多一次管线流程），每个三角形光栅化后仅写入深度而不做任何像素着色计算（不输出任何颜色），这样所有三角形通过第一个pass后，我们可以得到记录最小z值的屏幕深度图（实际就是z-buffer）；而第二个pass则作为正常渲染流程，只是每个三角形光栅化后需要关闭深度写入并通过比较深度（比较是否相等）来决定是否进行该像素的着色计算，这样就能保证屏幕每个像素只可能对应有最多一次像素着色计算。

总结Early-Z有如下特点：