目录
1.深度优先搜索
2.迷宫(经典深搜)
2.1 建图
2.2 深搜与回溯
2.3 完整代码
3.洛谷DFS
3.1 跳马
3.2 八皇后
3.2.1 建图
3.2.2 搜索
3.2.3 完整代码
3.3 Lake Counting(水坑计数)
今天主要来了解深度优先搜索(DFS)。
1.深度优先搜索
深搜的过程是从根节点进入,向下走,走到底再向上走,最后从根退出
深搜是通过系统栈实现的。
递归调用的过程,系统自动通过栈去维护函数的状态空间。
系统栈记录函数返回地址、局部变量、参数传递等。向下走,压栈;向上走,弹栈。
其实深搜就是枚举,暴力搜索而已。
2.迷宫(经典深搜)

输入
3 3 1
1 2 3 3
2 3输出
4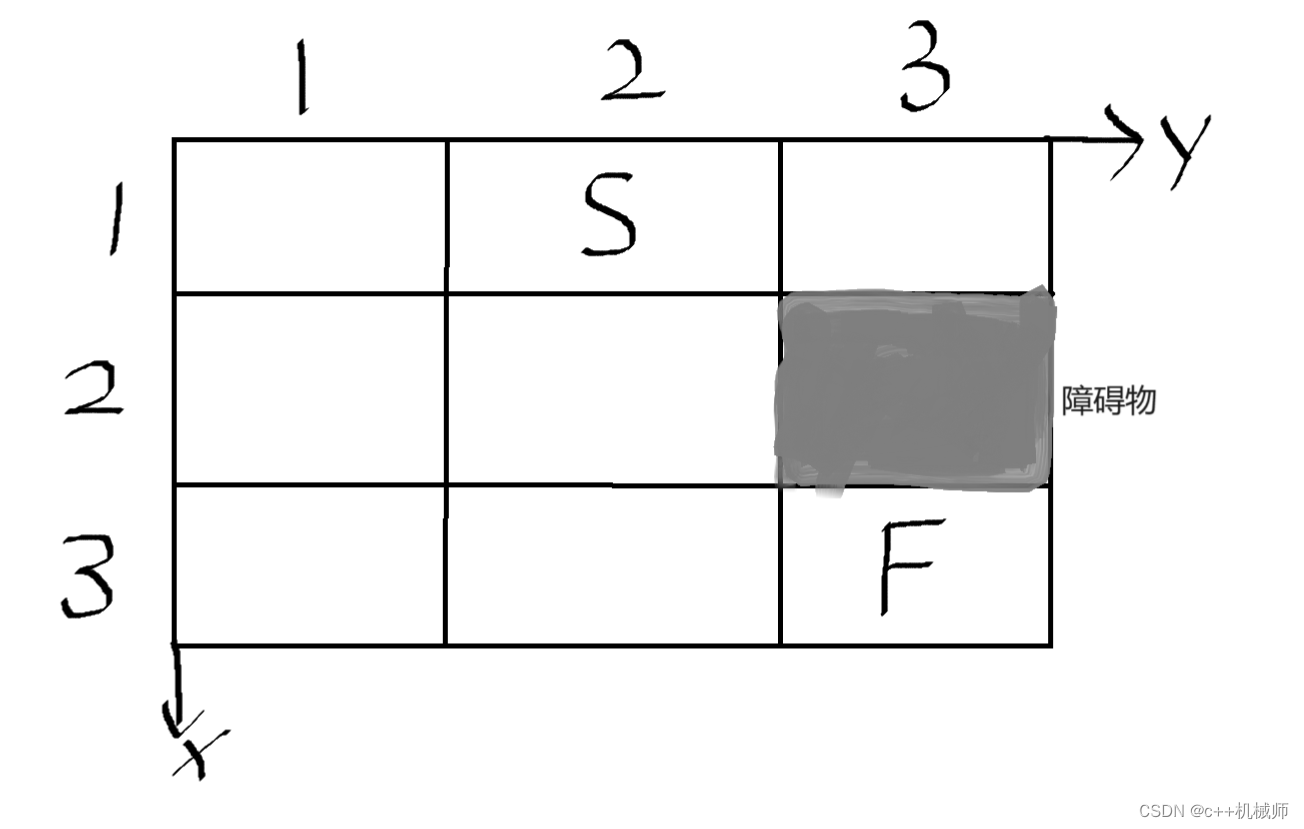
如图,起点坐标为(1,2),终点坐标为(3,3),障碍物坐标为(2,3),问我们从起点到终点有多少种走法,对于这种方案数的问题,正合DFS的口味,DFS就是通过暴力搜索、枚举所有可能的情况来找到答案,下面来看如何使用DFS:
2.1 建图
g[x][y]存入迷宫图,并进行判重
dx[4],dy[4]存方向偏移量,因为走到每个格子,我们又有四个方向可以走,需要枚举每个方向
格子就是点,格子到格子就是边
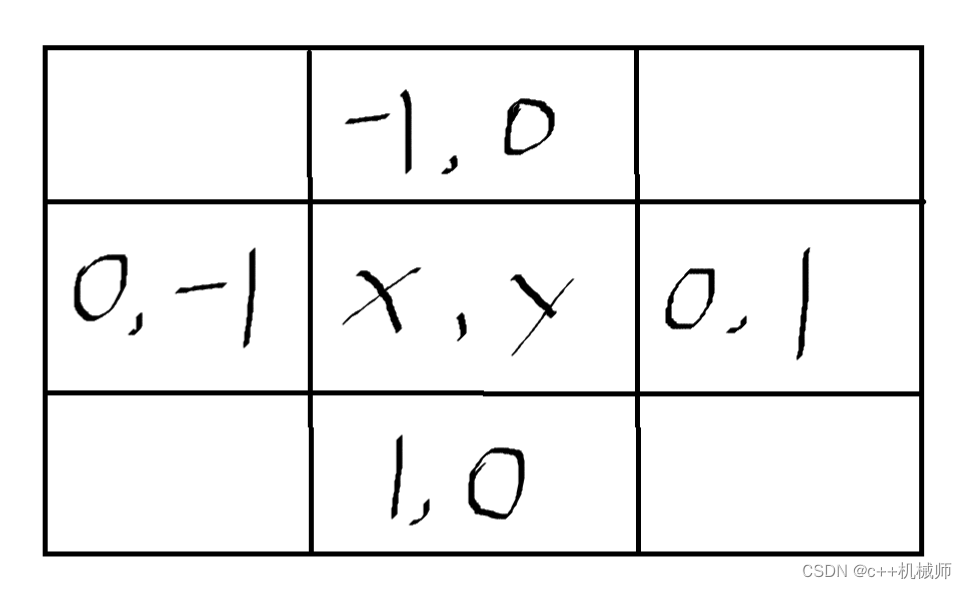
int m,n,t,sx,sy,fx,fy,a,b,ans;
int g[N][N];//存图并判重
int dx[4]={-1,0,1,0};//存方向偏移量
int dy[4]={0,1,0,-1};//存方向偏移量int main()
{cin>>n>>m>>t;//输入迷宫长度和障碍物总数cin>>sx>>sy>>fx>>fy;//输入起点和终点坐标for(int i=0;i<t;i++)cin>>a>>b,g[a][b]=1;//障碍物坐标,不能走,g[a][b]=1,表示已经走过,之后不会重复搜索,0表示还没有走过g[sx][sy]=1;//起点已经走过dfs(sx,sy);//从起点开始搜索cout<<ans;//输出答案return 0;
}2.2 深搜与回溯
从起点开始,四个方向进行搜索,能走就进行标记,锁定现场,然后走过去;一直走到无路可走就返回或者到达目的地,更新答案后返回,返回后要去除标记,恢复现场,之后还能继续走;继续尝试,直到枚举完所有可能,最后从入口退出。
void dfs(int x,int y)
{if(x==fx&&y==fy){ans++;return;}for(int i=0;i<4;i++){int a=x+dx[i],b=y+dy[i];if(a<1||a>n||b<1||b>m)continue;//坐标超出图的范围if(g[a][b])continue;//在本次搜索中已经走过了,不再进行下一步的搜索g[a][b]=1;//锁定现场dfs(a,b);//进行进一步的搜索g[a][b]=0;//恢复现场}
}深搜会生成DFS树:

2.3 完整代码
#include<iostream>
using namespace std;
const int N=10;
int m,n,t,sx,sy,fx,fy,a,b,ans;
int g[N][N];//存图并判重
int dx[4]={-1,0,1,0};//存方向偏移量
int dy[4]={0,1,0,-1};//存方向偏移量void dfs(int x,int y)
{if(x==fx&&y==fy){ans++;return;}for(int i=0;i<4;i++){int a=x+dx[i],b=y+dy[i];if(a<1||a>n||b<1||b>m)continue;//坐标超出图的范围if(g[a][b])continue;//在本次搜索中已经走过了,不再进行下一步的搜索g[a][b]=1;//锁定现场dfs(a,b);//进行进一步的搜索g[a][b]=0;//恢复现场}
}int main()
{cin>>n>>m>>t;//输入迷宫长度和障碍物总数cin>>sx>>sy>>fx>>fy;//输入起点和终点坐标for(int i=0;i<t;i++)cin>>a>>b,g[a][b]=1;//障碍物坐标,不能走,g[a][b]=1,表示已经走过,之后不会重复搜索,0表示还没有走过g[sx][sy]=1;//起点已经走过dfs(sx,sy);//从起点开始搜索cout<<ans;//输出答案return 0;
}3.洛谷DFS
3.1 跳马
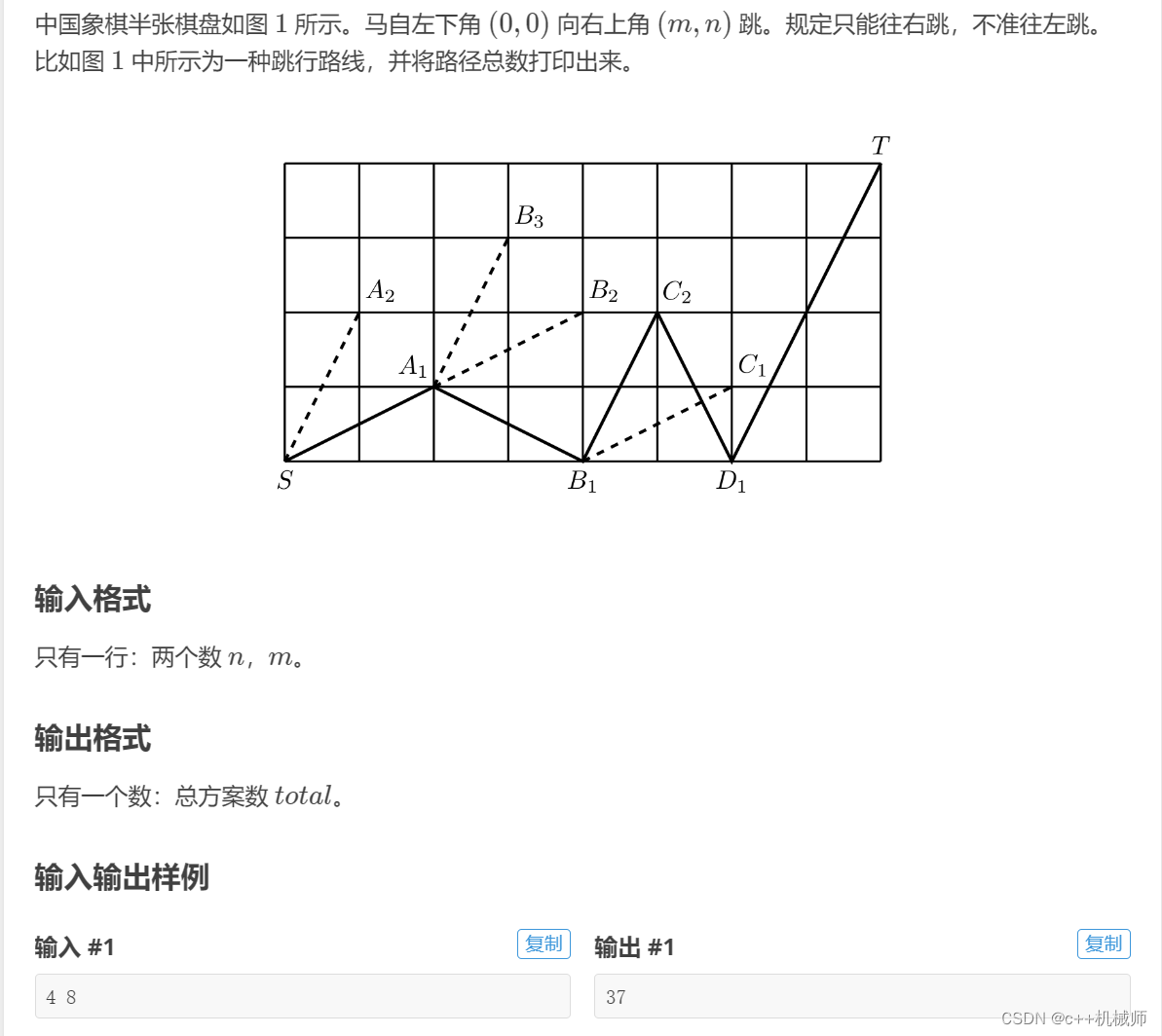
这个题和迷宫问题没什么区别,区别在于方向偏移量不一样,马只能走日,本来有八个方向,但只能往右上角跳,所以只有四个方向,同时因为不能向左跳,所以我们不用进行锁定现场和恢复现场进行判重,一直向右就完事了。
#include<iostream>
using namespace std;
int m,n,ans;
int dx[4]={2,1,-1,-2};
int dy[4]={1,2,2,1};void dfs(int x,int y)
{if(x==n&&y==m){ans++;return;}for(int i=0;i<4;i++){int a=x+dx[i],b=y+dy[i];if(a<0||a>n||b>m)continue;dfs(a,b);}
}int main()
{cin>>n>>m;dfs(0,0);cout<<ans;return 0;
}3.2 八皇后
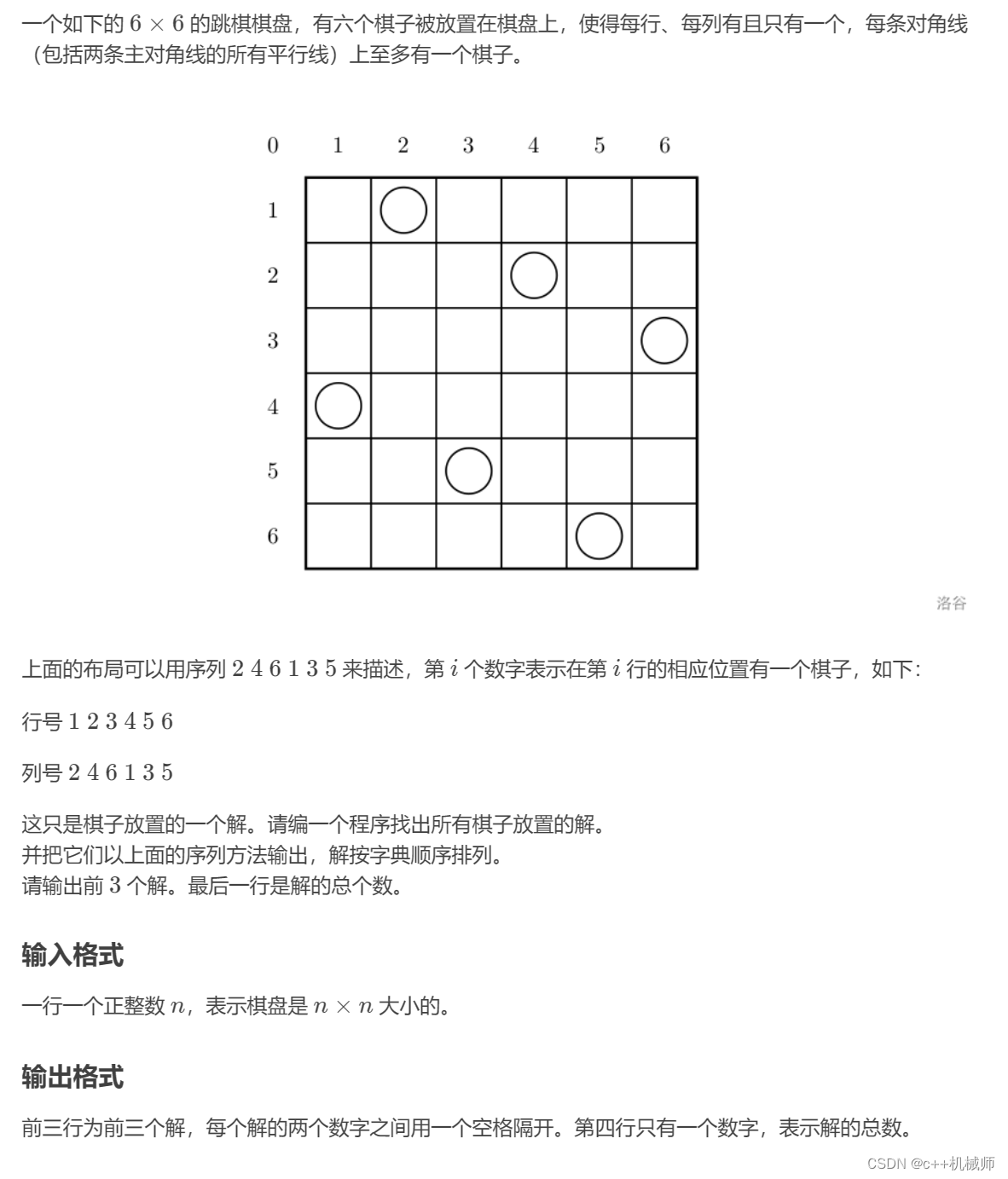

八皇后也是经典的DFS问题,也是方案数问题,以输入输出样例来看,简单来说就是每行每列每个对角线只能有一个皇后
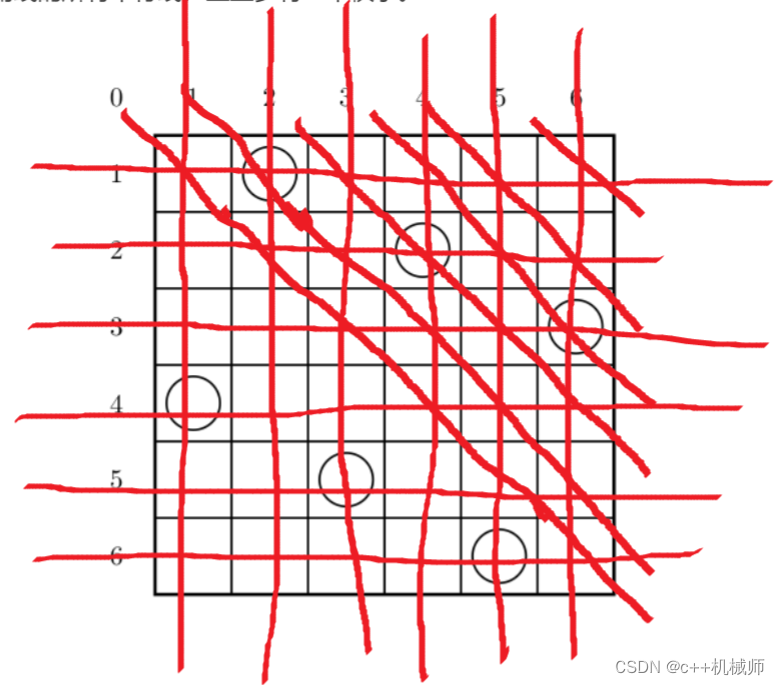
3.2.1 建图
pos数组记录各行放的位置。pos[1]=2
c数组标记列。c[2]=1
p数组标记撇对角线。p[1+2]=1 行列之和是定值(找行和列与对角线的映射关系)
q数组标记捺对角线。q[1-2+6]=1 行列之差是定值,防止下标为负数,都加上图的长度
p的下标(i+j) : 2,3,4,...,2n 范围
q的下标(i-j+n):1,2,3,...2n-1 范围
int n,ans;
int pos[N],c[N],p[N],q[N];//pos存每行皇后放在第几列int main()
{cin>>n;dfs(1);cout<<ans<<endl;return 0;
}3.2.2 搜索
从第一行开始放,之和尝试放2-n行。
对于第i行,依次枚举1-n列,如果第j列能放,记住该位置,记住其对角线和列,然后继续搜索第i+1行。
如果第i+1行的n列均不能放,则退回到第i行的状态,恢复现场,尝试第i行的下一列
如果能放满n行,说明找到了一种方案,则更新答案,返回上一行,继续搜索另一个合法方案,直到搜完所有可能方案
void print()
{if(ans<=3){for(int i=1;i<=n;i++)printf("%d ",pos[i]);puts("");}
}void dfs(int i)
{if(i>n){ans++;print();return;}for(int j=1;j<=n;j++)//枚举列{if(c[j]||p[i+j]||q[i-j+n])continue;pos[i]=j;//记录第i行放在了第j列c[j]=p[i+j]=q[i-j+n]=1;//宣布占领dfs(i+1);c[j]=p[i+j]=q[i-j+n]=0;//恢复现场}
}3.2.3 完整代码
#include<iostream>
using namespace std;
const int N=25;
int n,ans;
int pos[N],c[N],p[N],q[N];//pos存每行皇后放在第几列void print()
{if(ans<=3){for(int i=1;i<=n;i++)printf("%d ",pos[i]);puts("");}
}void dfs(int i)
{if(i>n){ans++;print();return;}for(int j=1;j<=n;j++)//枚举列{if(c[j]||p[i+j]||q[i-j+n])continue;pos[i]=j;//记录第i行放在了第j列c[j]=p[i+j]=q[i-j+n]=1;//宣布占领dfs(i+1);c[j]=p[i+j]=q[i-j+n]=0;//恢复现场}
}
int main()
{cin>>n;dfs(1);cout<<ans<<endl;return 0;
}3.3 Lake Counting(水坑计数)
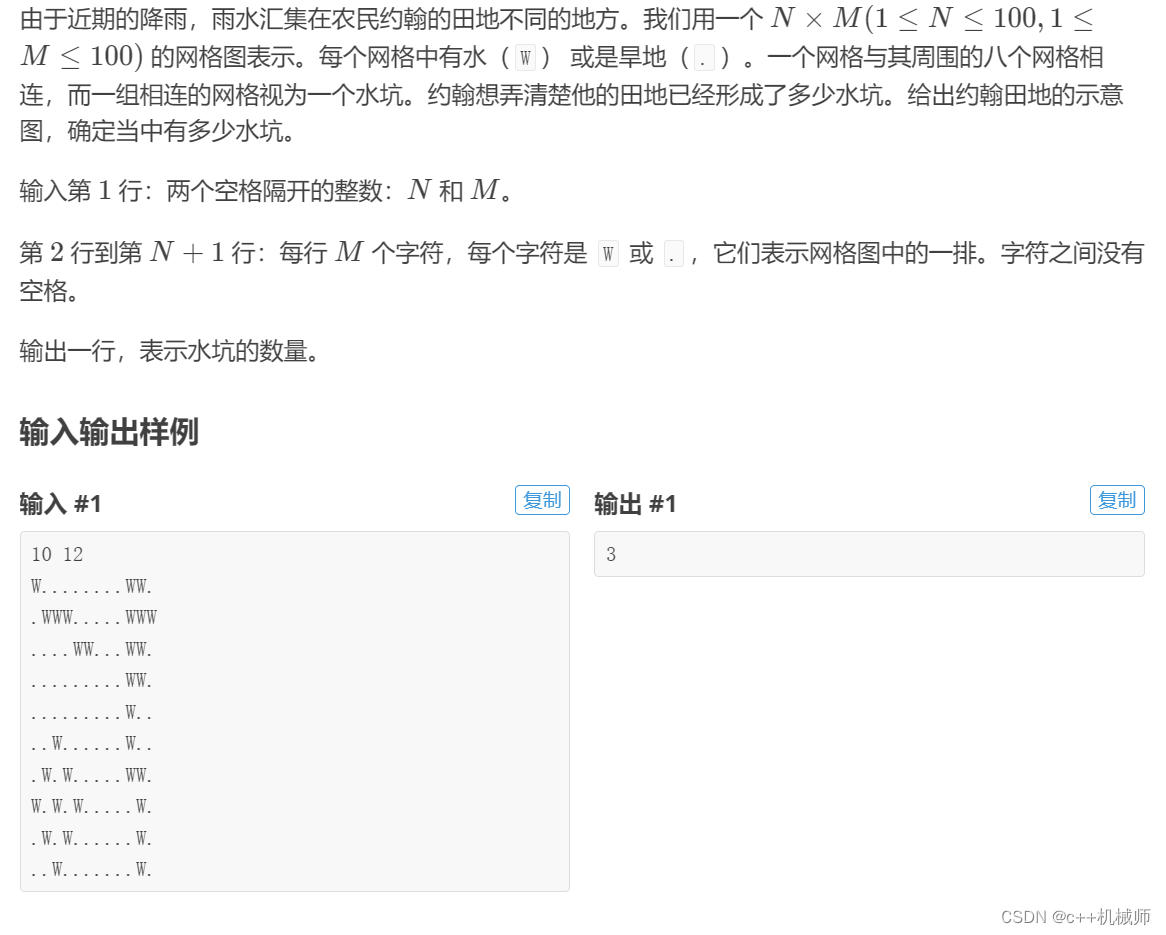
这个是DFS的另一个经典应用,连通块问题 ,如果一个网格有水,则周围的八个网格和这个网格就视为一个水坑,这个很明显也是要存方向偏移量,很明显的DFS,而且很明显是不需要回溯的,能连通就能,不能就放弃,只需要判重防止重复搜索就行了。
#include<iostream>
using namespace std;
const int N=110;
int n,m,ans;
char g[N][N];
int dx[8]={-1,-1,-1,0,1,1,1,0};
int dy[8]={-1,0,1,1,1,0,-1,-1};void dfs(int x,int y)
{g[x][y]='.';for(int i=0;i<8;i++){int a=x+dx[i],b=y+dy[i];if(a<0||a>=n||b<0||b>=m)continue;if(g[a][b]=='.')continue;dfs(a,b);}
}
int main(){cin>>n>>mfor(int i=0;i<n;i++)cin>>g[i];for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(g[i][j]=='W'){dfs(i,j);ans++;}}}cout<<ans;return 0;
}