对各种数据结构的感受

树状数组：

可以用来维护前缀的，满足交换律的东西？
方便好写，常数极小，但使用范围不广。
其实二分套树状数组可以通过倍增来做到 \(O(\log n)\) 的。

并查集：

可以用来维护一些联通块，无论是数值的还是位置上的。
特征也比较明显，因为应该没人写 ds 时维护 bfs 的状态吧！
要求是必须只关心整个块的信息，不能关心某几个跟他链接的点的信息。
常数也很小，不亚于树状数组。

线段树：

算是一种非常常用的数据结构了。
可以在 \(O(merge) \log n\) 的时间复杂度内完成任何满足交换律的东西。
一些技巧：

大多数二分套线段树可以被线段树二分/单侧递归线段树等来做到 \(O(\log)\)。

线段树合并 \(n\) 个大小为 \(n\) 的集合的时间复杂度为 \(O(n \log n)\)，可以通过势能分析。

动态开点线段树：是一种时间，空间都比较劣的线段树，但可以支持范围很大，重要的点较少的线段树。

主席树：

就是可持久化线段树，可以快速地在空间，时间都为 \(O(n \log n)\) 地限制内求出类似查询区间不同数地数量这种较复杂的东西的线段树，比线段树的优势在于可以支持区间求数值的操作。
一般是维护地权值线段树，然后建 \(n\) 棵线段树。

但主席树不支持修改，如果是动态区间第 k 大的话就得树套树，外层再套一个树状数组。

主席树有懒标记的话得开 3 倍空间。

猫树：

离线的线段树。
猫树的优势在于，只要线段树能做的无强制在线的，猫树几乎都能做。
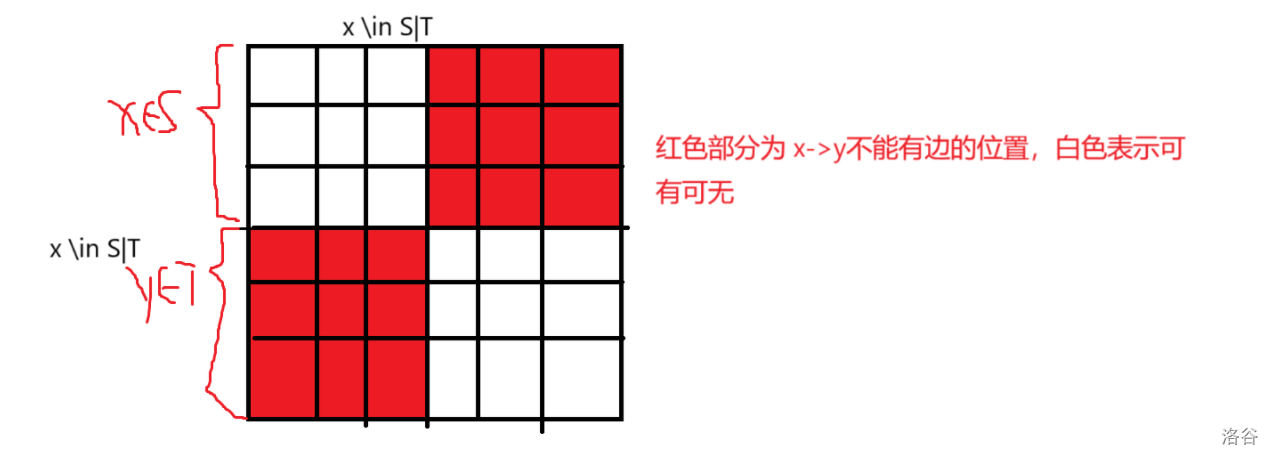
大体思路就是离线，然后分治，对于每个 \(x \in l \sim mid\) 且 \(y \in mid + 1 \sim r\) 的查询，预处理出左边的每一个后缀，右边的每一个前缀，再暴力合并即可。
往往能达到很好的效果。

平衡树：

treap 感觉没什么用，因为不支持区间操作。
FHQ 的本质就是通过很多次分裂于合并让树高不会太高。
Splay 的本质是时间复杂度均摊，每次将询问的点旋到根，且复杂度严格 \(log\)，也就是因为复杂度均摊，所以 LCT 用 Splay 的话是单 log。
支持 reverse 操作。

分块：

比较全能的数据结构。
他对于线段树的优势在于：能做更多的操作。
有的时候线段树不方便下传标记，或者将多个标记合并时，就可以考虑分块。
前面分块唯一不能取代的就是不支持 reverse 操作。
且分块的常数和时间复杂度都不小。
谨慎使用。

莫队：

也是一种离线算法。
本质就是当你直接做不好做，且知道 \(l,r\) 之后就能知道 \(l,r+1\) 类似这种东西时可以考虑莫队。