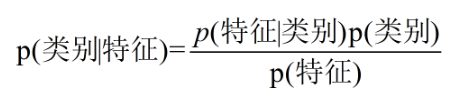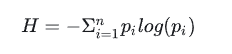人工智能原理实验4（2）——贝叶斯、决策求解汽车评估数据集-编程知识

🧡🧡实验内容🧡🧡

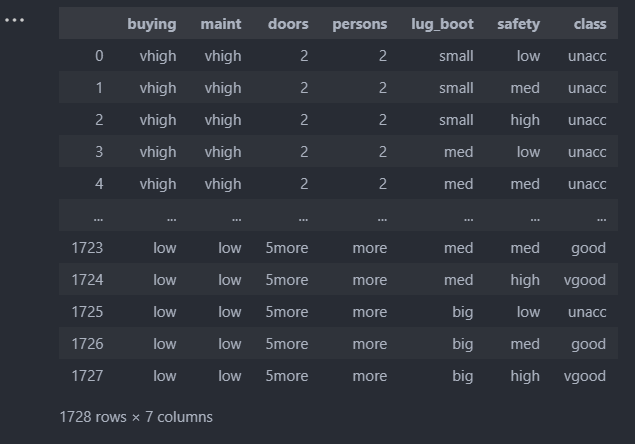
汽车数据集
车子具有 buying,maint,doors,persons,lug_boot and safety六种属性，而车子的好坏分为uncc,ucc,good and vgood四种。

🧡🧡贝叶斯求解🧡🧡

数据预处理

1.转为数字编码
将数据集中的中文分类编码转为数字编码，以便更好地训练。这里采用sklearn的LabelEncoder库进行快速转换。

2.拆分数据集
按7：3的比例拆出训练集和测试集，这里也采用sklearn的train_test_split快速拆分，比手动拆分能更具随机性

3.将dataframe对象转为array
在手动实现的贝叶斯算法类中，通过numpy可以很方便的操纵和计算矩阵格式的数据，因此通过dataframe对象导入数据后，通过df.values将其转为array

朴素贝叶斯原理

核心公式：

对于二分类问题，在已知样本特征的情况下，分别求出两个分类的后验概率：P（类别1 | 特征集），P（类别2 | 特征集），选择后验概率最大的分类作为最终预测结果。
为何需要等式右边？
对于某一特定样本，很难直接计算它的后验概率（左边部分），而根据贝叶斯公式即可转为等式右边的先验概率（P（特征）、P（类别））和条件概率（P（特征 | 类别）），这些可以直接从原有训练样本中求得，其次，由于最后只比较相对大小，因此分母P（特征）在计算过程中可以忽略。
右边P（特征 | 类别）和P（特征）如何求？
例如，对于car-evalution这个数据集，假设特征只有doors、persons、safety，目标为class。
对于某个样本，它的特征是doors=2、persons=3、safety=low。
则它是unacc的概率是
P(unacc | doors=2、persons=3、safety=low) =
P(doors=2、persons=3、safety=low | unacc) * P(unacc) / P(doors=2、persons=3、safety=low)
对于P(unacc)，即原训练样本集中的unacc的频率。
对于P(doors=2、persons=3、safety=low | unacc)，并不是直接求原训练样本集中满足unacc条件下，同时为doors=2、persons=3、safety=low的概率，这样由于数据的稀疏性，很容易导致统计频率为0，因此朴素贝叶斯算法就假设各个特征直接相互独立，即
P(doors=2、persons=3、safety=low | >unacc) = P(doors=2 | unacc)*P(persons=3 |unacc)*P(safety=low | unacc)，朴素一词由此而来。
对于P(doors=2、persons=3、safety=low) ，同上述，其等于P(doors=2)*P(persons=3)*P(safety=low)

代码

import pandas as pd
df=pd.read_excel("data/car_data1.xlsx")# ==================数据预处理==================
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
le=LabelEncoder()
for i in df.columns:df[i]=le.fit_transform(df[i])
# df
X=df[df.columns[:-1]]
y=df['class']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)#三七开
X_train=X_train.values
X_test=X_test.values
y_train=y_train.values
y_test=y_test.values# ==================朴素贝叶斯==================
import numpy as np
from sklearn.metrics import accuracy_score
class NaiveBayes:def fit(self, X, y):self.X = Xself.y = yself.classes = np.unique(y) # 目标分类名称集：（0 、 1），ex：嫁、不嫁self.prior_probs = {} # 先验概率self.cond_probs = {} # 条件概率# 计算先验概率——分子项 P(类别)， ex：P(嫁)、P(不嫁)for c in self.classes:self.prior_probs[c] = np.sum(y == c) / len(y)# 计算条件概率——分子项 P(特征/类别)， ex：P(帅、性格好、身高矮、上进 | 嫁)for feature_idx in range(X.shape[1]): # 0....featureNum 表示每一列特征索引，ex：是否帅、是否性格好、身高程度、上不上进self.cond_probs[feature_idx] = {}for c in self.classes:feature_values = np.unique(X[:, feature_idx]) # featureValue1、featureValue2、...ex：帅、不帅self.cond_probs[feature_idx][c] = {}for value in feature_values:idx = (X[:, feature_idx] == value) & (y == c) # [0,1,0,0,0.......]self.cond_probs[feature_idx][c][value] = np.sum(idx) / np.sum(y == c) # ex：P[是否帅][嫁][帅]def predict(self, X_test):pred_label = []pred_scores = []# 对每个测试样本进行预测for x in X_test:posterior_probs = {}# 计算后验概率——P(嫁|帅、性格好、身高矮、上进) 和 P(不嫁|帅、性格好、身高矮、上进)for c in self.classes:posterior_probs[c] = self.prior_probs[c]for feature_idx, value in enumerate(x):if value in self.cond_probs[feature_idx][c]:posterior_probs[c] *= self.cond_probs[feature_idx][c][value]# 选择后验概率最大的类别作为预测结果predicted_class = max(posterior_probs, key=posterior_probs.get) # 获得最大的value对应的keypred_score = posterior_probs[predicted_class] # 获得最大的valuepred_label.append(predicted_class)pred_scores.append(pred_score)return pred_label, pred_scores# ==================训练+预测==================
nb = NaiveBayes()
nb.fit(X_train, y_train)
y_pred, y_scores = nb.predict(X_test)# ==================评估==================
import matplotlib.pyplot as plt
import seaborn as sns# 混淆矩阵
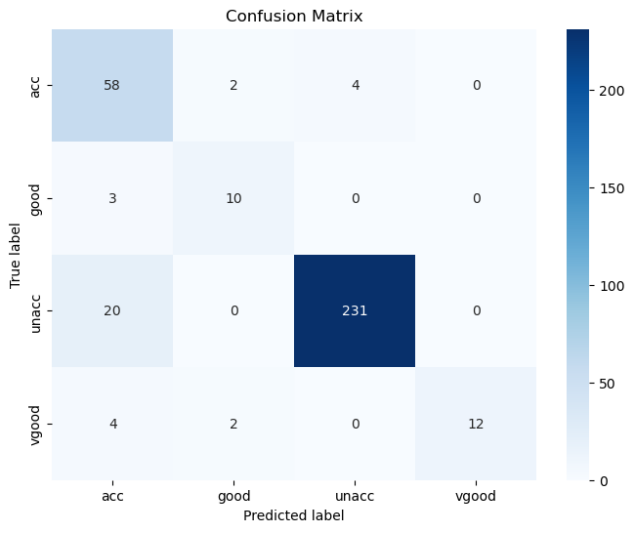
def cal_ConfusialMatrix(y_true_labels, y_pred_labels):cm = np.zeros((4, 4))for i in range(len(y_true_labels)):cm[ y_true_labels[i], y_pred_labels[i] ] += 1plt.figure(figsize=(8, 6))sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['acc','good','unacc', 'vgood'], yticklabels=['acc','good','unacc', 'vgood'])plt.xlabel('Predicted label')plt.ylabel('True label')plt.title('Confusion Matrix')plt.show()
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率：", accuracy)
y_pred=[int(x) for x in y_pred]
cal_ConfusialMatrix(y_test, y_pred)

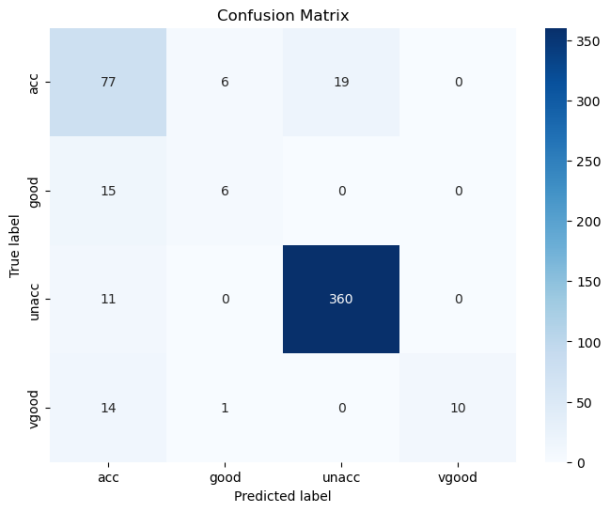
结果

在这里插入图片描述

🧡🧡决策树算法求解🧡🧡

数据预处理：

和上述贝叶斯算法中的数据预处理基本一致，这里因为计算信息熵时，要根据信息熵的收敛精度才决定是否跳出递归，经过几次尝试，选择将训练集和测试集8:2的比例拆分，并且random_state=10，避免随机性导致程序死循环。

决策树原理

决策树的决策流程就是从所有输入特征中选择一个特征做为决策的依据，找出一个阈值来决定将其划分到哪一类。
也就是说，创建一个决策树的主要问题在于：
1.决策树中每个节点在哪个维度的特征上面进行划分？
2.被选中的维度的特征具体在哪个值上进行划分？
信息熵的计算公式：
其中n是指数据中一共有n类信息，pi就是指第i类数据所占的比例。
信息熵简单的来说就是表示随机变量不确定度的度量。
熵越大，数据的不确定性就越大。
熵越小，数据的不确定性就越小，也就是越确定。

举个例子
假设我们的数据中一共有三类。每一类所占比例为1/3，那么信息熵就是：
假设我们数据一共有三类，每类所占比例是0，0，1，那么信息熵就是：
（实际上log（0）是不能计算的，定义上不允许，程序中直接置为inf即可）
很显然第二组数据比第一组数据信息熵小，也就是不确定性要少，换句话讲就是更为确定。
我们希望决策树每次划分数据都能让信息熵降低，当划分到最后一个叶子节点里面只有一类数据的时候，信息熵就自然的降为了0，所属的类别就完全确定了。
那么怎样找到一个这样的划分使得划分后的信息熵会降低？对着所有维度的特征来一次搜索就行了。

代码

import pandas as pd
import numpy as np
from collections import Counter
from math import logdf=pd.read_excel("data/car_data1.xlsx")# ==================数据预处理==================
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
le=LabelEncoder()
for i in df.columns:df[i]=le.fit_transform(df[i])
# df
X=df[df.columns[:-1]]
y=df['class']
X = X.astype(float)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10) #二八开
X_train=X_train.values
X_test=X_test.values
y_train=y_train.values
y_test=y_test.values# ==================决策树==================
class Node:def __init__(self,x_data, y_label, dimension, value):self.x_data = x_dataself.y_label = y_labelself.dimension = dimensionself.value = valueself.left = Noneself.right = Noneclass DTree:def __init__(self):self.root = Nonedef fit(self,x_train, y_train):def entropy(y_label):counter = Counter(y_label)ent = 0.0for num in counter.values():p = num / len(y_label)ent += -p * log(p)return entdef one_split(x_data, y_label):best_entropy = float('inf')best_dimension = -1best_value = -1for d in range(x_data.shape[1]):sorted_index = np.argsort(x_data[:, d])for i in range(1,len(x_data)):if x_data[sorted_index[i], d] != x_data[sorted_index[i - 1], d]:value = (x_data[sorted_index[i], d] + x_data[sorted_index[i-1], d]) / 2x_left, x_right, y_left, y_right = split(x_data, y_label, d, value)p_left = len(x_left) / len(x_data)p_right = len(x_right) / len(x_data)ent = p_left * entropy(y_left) + p_right * entropy(y_right)if ent < best_entropy:best_entropy = entbest_dimension = dbest_value = valuereturn best_entropy, best_dimension, best_valuedef split(x_data, y_label, dimension, value):"""x_data:输入特征y_label:输入标签类别dimension:选取输入特征的维度索引value：划分特征的数值return 左子树特征，右子树特征，左子树标签，右子树标签"""index_left = (x_data[:,dimension] <= value)index_right = (x_data[:,dimension] > value)return x_data[index_left], x_data[index_right], y_label[index_left], y_label[index_right]def create_tree(x_data, y_label):ent, dim, value = one_split(x_data, y_label)x_left, x_right, y_left, y_right = split(x_data, y_label, dim, value)node = Node(x_data, y_label, dim, value)if ent < 0.3:return nodenode.left = create_tree(x_left, y_left)node.right = create_tree(x_right, y_right)return nodeself.root = create_tree(x_train, y_train)return selfdef predict(self,x_predict):def travel(x_data, node):p = nodeif x_data[p.dimension] <= p.value and p.left:pred = travel(x_data, p.left)elif x_data[p.dimension] > p.value and p.right:pred = travel(x_data, p.right)else:counter = Counter(p.y_label)pred = counter.most_common(1)[0][0]return predy_predict = []for data in x_predict:y_pred = travel(data, self.root)y_predict.append(y_pred)return np.array(y_predict)def score(self,x_test,y_test):y_predict = self.predict(x_test)return np.sum(y_predict == y_test) / len(y_predict), y_predictdef __repr__(self):return "DTree(criterion='entropy')"# =================训练=================
dt = DTree()
dt.fit(X_train, y_train)# ==================评估==================
import matplotlib.pyplot as plt
import seaborn as sns
# 混淆矩阵
def cal_ConfusialMatrix(y_true_labels, y_pred_labels):cm = np.zeros((4, 4))for i in range(len(y_true_labels)):cm[ y_true_labels[i], y_pred_labels[i] ] += 1plt.figure(figsize=(8, 6))sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['acc','good','unacc', 'vgood'], yticklabels=['acc','good','unacc', 'vgood'])plt.xlabel('Predicted label')plt.ylabel('True label')plt.title('Confusion Matrix')plt.show()
accuracy, y_pred = dt.score(X_test,y_test)
print("准确率：", accuracy)
y_pred=[int(x) for x in y_pred]
cal_ConfusialMatrix(y_test, y_pred)