目录
- 一、二叉树的创建(伪)
- 二、二叉树的遍历
- 2.1 前序遍历
- 2.2 中序遍历
- 2.3 后序遍历
- 三、二叉树节点个数及高度
- 3.1 二叉树节点个数
- 3.2 二叉树叶子节点个数
- 3.3二叉树第k层节点个数
- 3.4 二叉树查找值为x的节点
- 四、二叉树的创建(真)
一、二叉树的创建(伪)
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,且为了方便后面的介绍,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
基于二叉树的链式结构,于是可以先malloc动态开辟出二叉树的每个节点并初始化,然后通过节点中的指针struct BinaryTreeNode* left(指向左树)和struct BinaryTreeNode* right(指向右树),将各个节点连接起来,最后大致模拟出了一棵二叉树,代码如下:
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left; //左树struct BinaryTreeNode* right; //右树
}BTNode;
BTNode* CreatBinaryTree()
{//动态开辟节点BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//链接节点node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
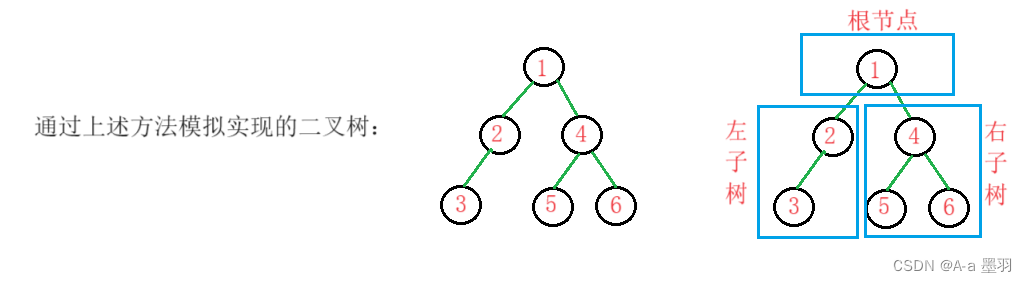
在实现二叉树基本操作前,再回顾下二叉树的概念,一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵分别称为左子树和右子树的二叉树组成
二叉树满足的条件:
- 二叉树不存在度大于2的结点;
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
其余二叉树的概念还请回顾:【数据结构和算法】—二叉树(1)–树概念及结构
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
注意: 上述代码并不是创建二叉树的方式,真正创建二叉树方式将在后面介绍。
二、二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。 访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。下图可以理解为是二叉树的前序遍历:

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。 NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
2.1 前序遍历
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。 依据此规律我们便可如下遍历二叉树,为了方便观察,每次遍历到根节点都输出一下:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){putchar('N');return;}putchar(root->val); //访问根节点BinaryTreePrevOrder(root->left); //访问左子树BinaryTreePrevOrder(root->right); //访问右子树
}
前序遍历代码,逻辑结构大致如下图,可以参考一下:
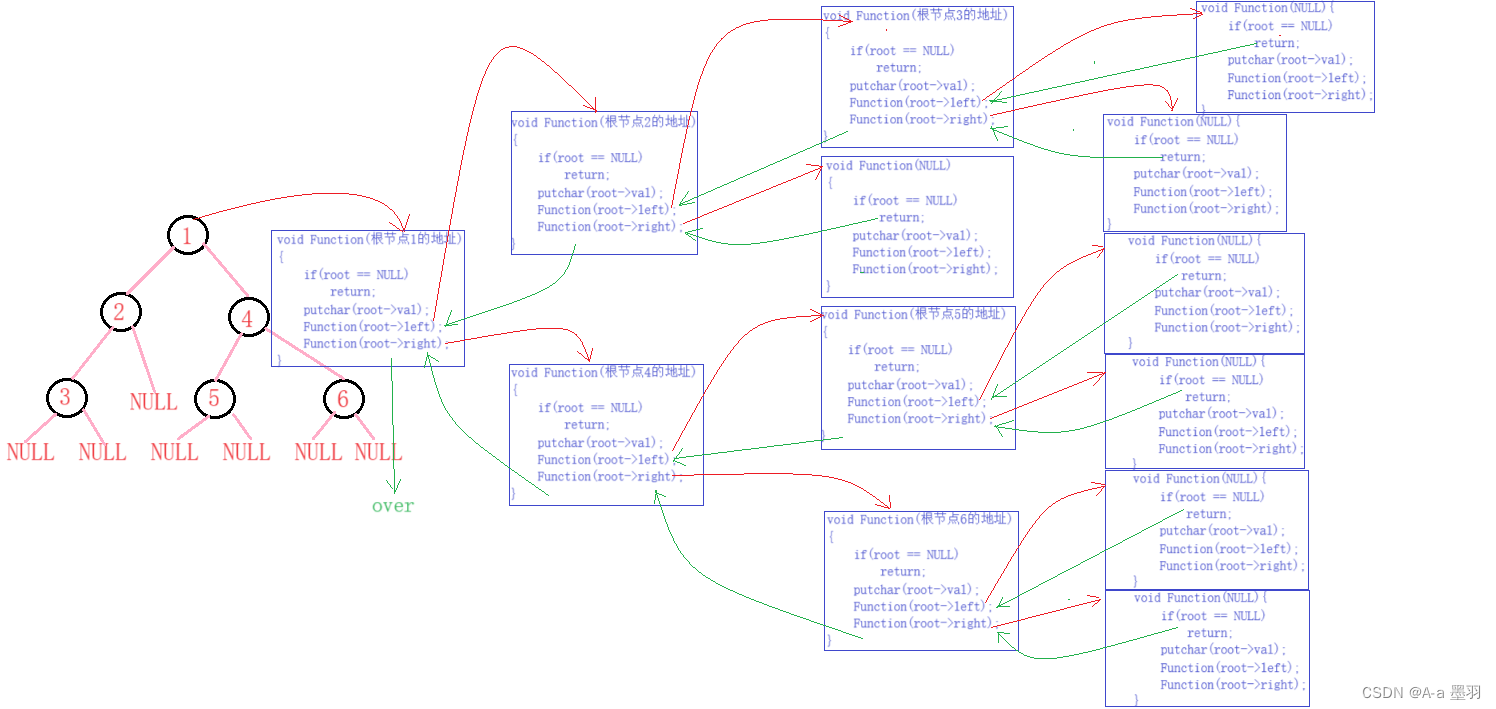
在这利用递归思想来解决前序遍历的问题,因为是前序遍历(访问顺序依次是根节点,左子树,右子树),所以在进入下层递归前可以先输出根节点。当进入左/右子树时,会更新根节点(原为上层根节点的左/右孩子节点) 。二叉树的叶子节点的左右孩子都为NULL,那么便可将递归的结束条件定为NULL。这便是前序遍历的递归逻辑。
2.2 中序遍历
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。 与前序遍历相似,只是访问顺序不同(依次是左子树,根节点,右子树),那么调整一下代码顺序即可,将输出根节点值的操作(putchar(root->val);),放在访问左子树之后。那么递归每次都会先进入左子树,且最先打印的为叶子节点。代码如下:
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){putchar('N');return;}BinaryTreeInOrder(root->left); //访问左子树putchar(root->val); //输出根节点BinaryTreeInOrder(root->right); //访问右子树
}
2.3 后序遍历
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。 同样与前序遍历相似,访问顺序不同(依次是左子树,右子树,根节点),依此特性所以我们只需将输出操作(putchar(root->val))放到最后,其余代码不变。实现思想-递归完左子树和右子树后再输出根节点。 代码如下:
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){putchar('N');return;}BinaryTreePostOrder(root->left); //访问左子树BinaryTreePostOrder(root->right); //访问右子树putchar(root->val); //输出根节点
}
三种遍历最后输出的结果(图中N表示递归时遇到了NULL):
- 前序遍历结果:1 2 3 4 5 6
- 中序遍历结果:3 2 1 5 4 6
- 后序遍历结果:3 2 5 6 4 1

- 设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为 ( D )。
A adbce
B decab
C debac
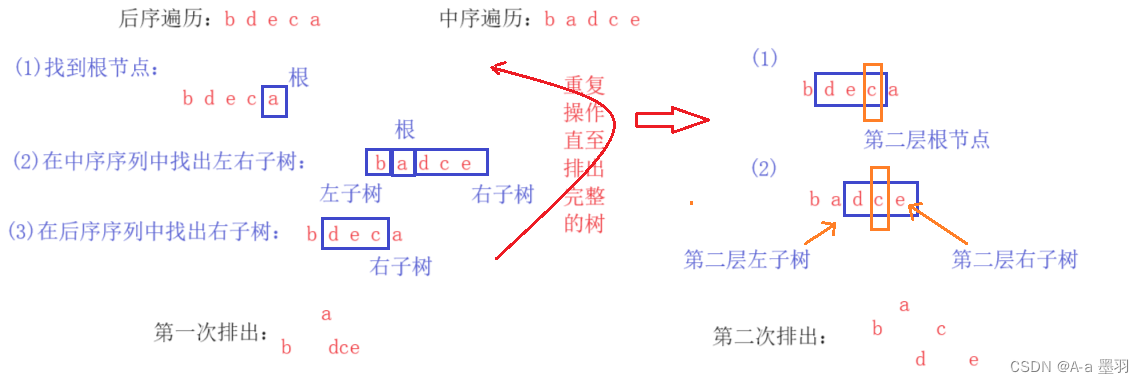
D abcde解: 解题思想(给定两种遍历序列,求出另外一种):我们可以根据各种遍历方法的特性来求解。( 1 ) 根据后续遍历序列找出根节点,因为后续遍历最后才会输出根,那么在序列的最后一个即为根节点
a;( 2 ) 接着在中序遍历序列中找出根节点,然后划分左子树和右子树;( 3 ) 然后再到后序遍历序列中去除左子树和根节点,那么得到的便是右子树,并将其看为独立的树;( 4 ) 重复上述三步操作,直到排出完整的树。
图解如下:
解决此类问题最重要的还是要弄懂代码的递归思想。
三、二叉树节点个数及高度
3.1 二叉树节点个数
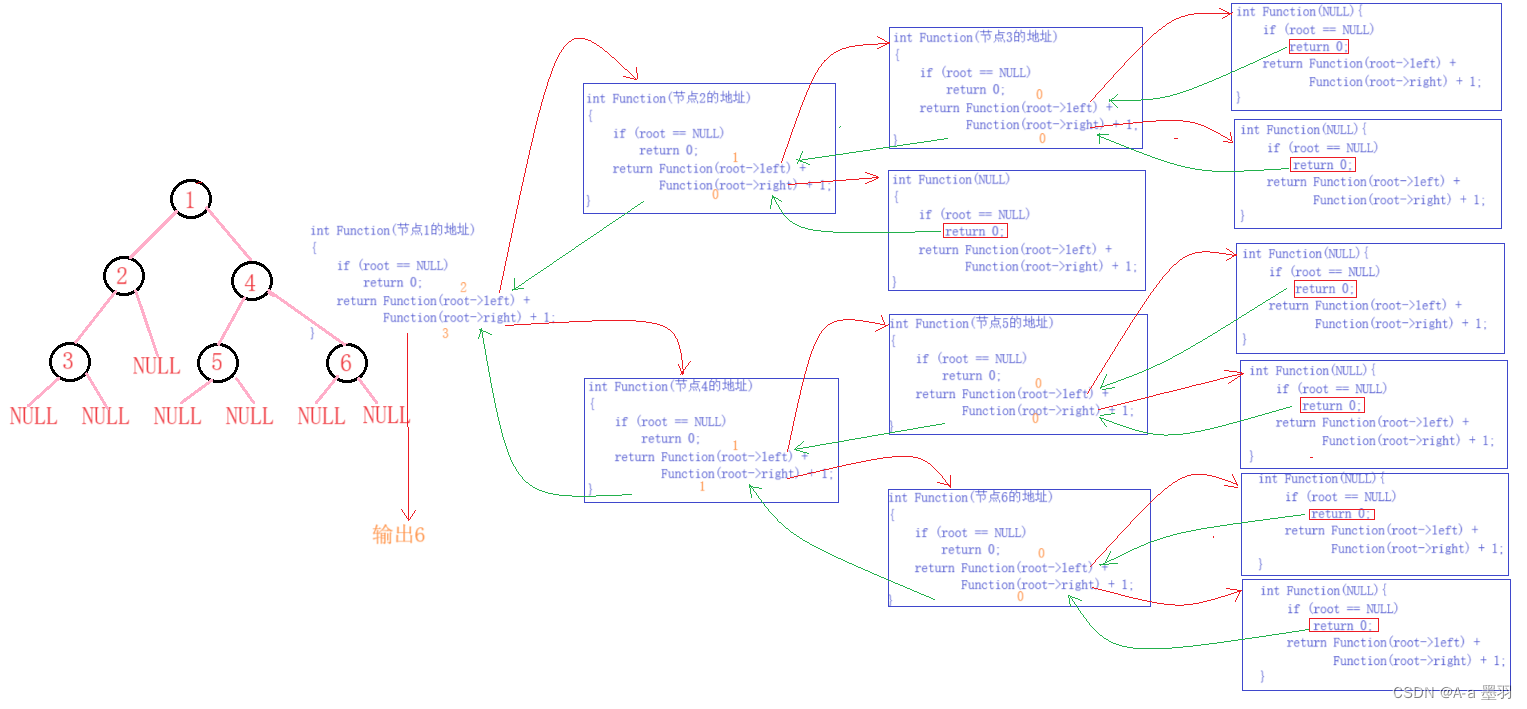
求二叉树的节点个数,利用的还是递归思想。我们可以将问题转化为----根节点(1),左子树的节点个数(root->left)和右子树的节点个数(root->right)的总结点个数。我们可以将根节点为空(root == NULL)作为递归结束的条件,并返回0(return 0)。 这种方法通常被称为递归分治。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
代码图解:
3.2 二叉树叶子节点个数
叶子节点概念:含有的子树个数为0的节点。 如本次创建的二叉树的节点3,节点5,节点6。
基于叶子节点的特性,同样可以利用递归分治的方法,将问题同化为----左子树的叶子节点个数和右子树的叶子节点个数之和。
函数返回的条件:
- 当前节点(
root)的左子树(root->left)和右子树(root->right)都为空时(即!(root->left && root->right)),那么此节点为叶子节点,并返回1; - 当前节点为空节点(即
(root == NULL)),返回0; - 函数执行到最后,返回当前树的叶子节点数。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (!(root->left && root->right))return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
代码图解:
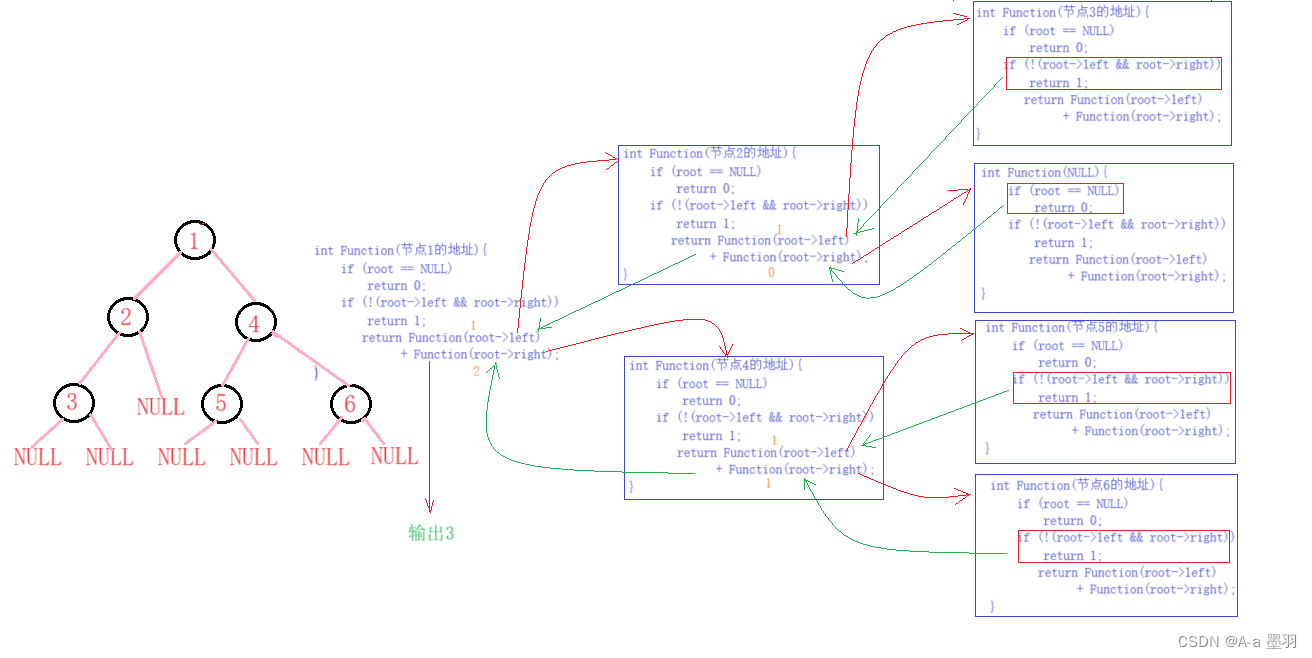
3.3二叉树第k层节点个数
既然是求第k层的节点个数,那我们便可以定义一个变量k,记录当前函数所要递归的层数。既然k的值是变化的,那么可以将他作为函数的参数,每递归一层便让他减一k - 1,那么当k的值到1时,便是我们所要求的二叉树的第k层。
依据上述关系,便可以得出 函数返回的条件:
- 当遇到空节点时(
root == NULL),返回0; - 当
k == 1时(说明到了二叉树的第k层),且当前节点不为空(root != NULL),那么便可返回1; - 函数执行到了最后,返回统计到的符合条件的节点个数。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1 && root != NULL)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
根据函数返回条件不难发现,当k == 1时递归便不会继续往下层执行,这是因为此时函数必定会满足两个if条件中的一个,这也避免了递归到二叉树的第k + 1层。
代码图解:
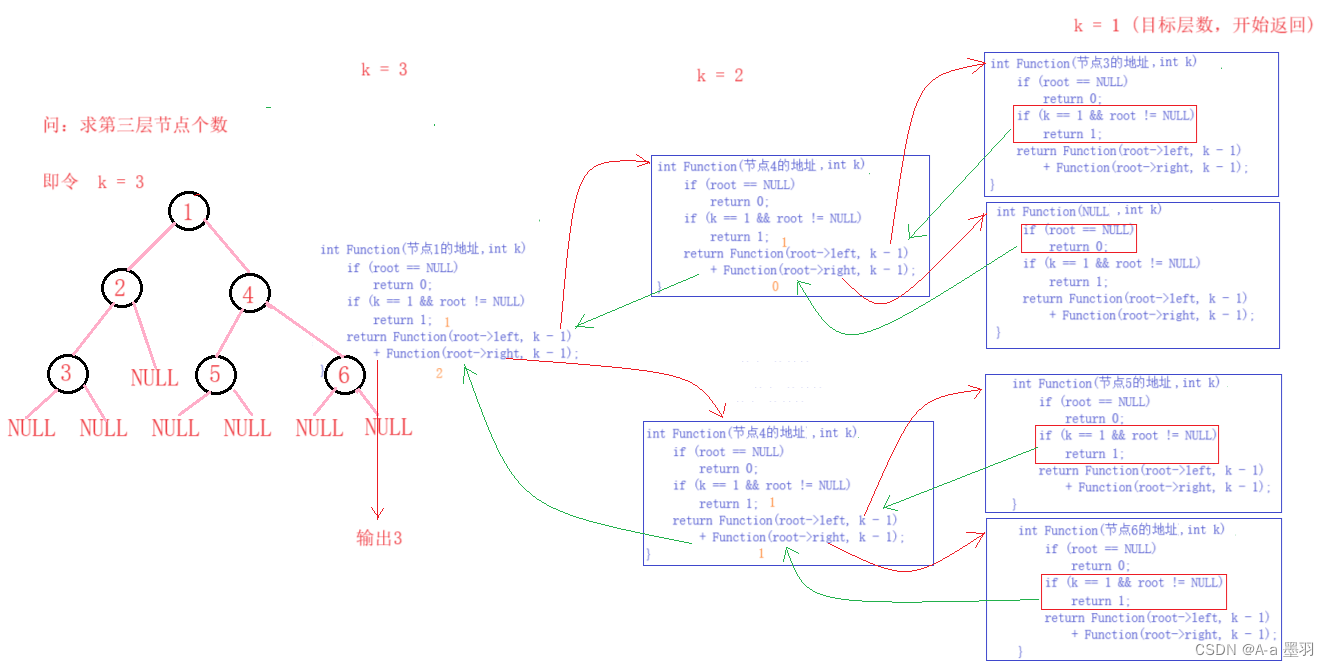
3.4 二叉树查找值为x的节点
查找值为x的节点,可以将递归分治为----判断当前节点,判断左子树,判断右子树。 那么当遇到空节点(root == NULL)就返回return NULL;如果遇到所要查找的值(root->val == x)就返回当前地址(return root);那么如果都不满足就继续搜寻左子树,然后右子树;直到最后搜寻完整棵二叉树,都没有找到x,那么便返回NULL。
还需要注意的一个问题是,如果在递归过程中找到了目标值x,返回了当前地址root,但是现在只是回到了上一层递归的地方,返回值并不会被接收,而是继续执行下一个逻辑。 那么我们便可以用BTNode* ret1来接受函数的返回值,并判断,当返回值(ret1)不为NULL时(即说明上一次递归时,找到了x)直接返回此值return ret1。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{//空节点if (root == NULL)return NULL;//值为x的节点if (root->val == x)return root;//左子树递归,ret接收返回值,并判断BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1 != NULL)return ret1;//方法一:易于理解//BTNode* ret2 = BinaryTreeFind(root->right, x);//if (ret2 != NULL)// return ret2;return BinaryTreeFind(root->right, x);return NULL;
}
代码图解:
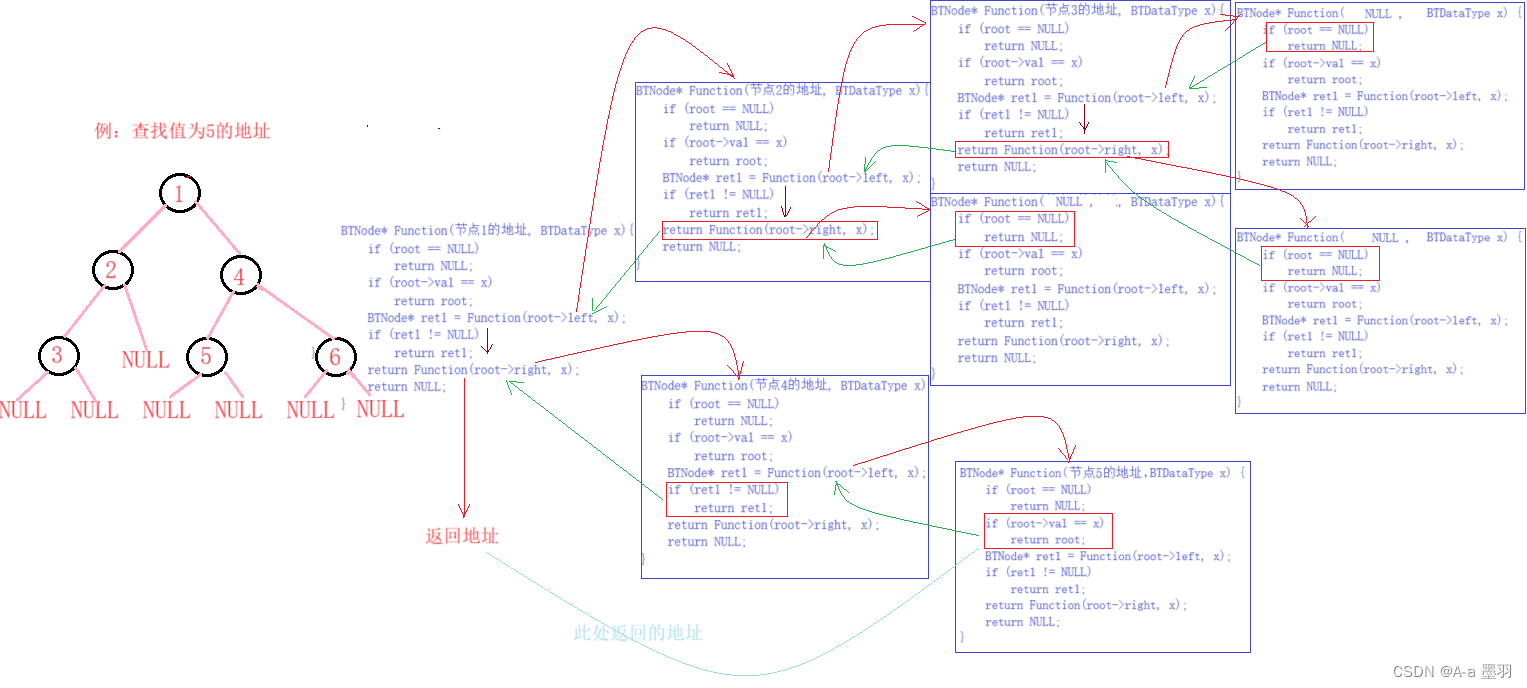
四、二叉树的创建(真)
通过上面对各种遍历方法和递归思想的讲解,相信使用递归来真正创建二叉树也不难了,如下:
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{//判断是否为空,即当a[*pi] == '#'时if (a[*pi] == '#'){(*pi)++;return NULL;}//动态开辟节点BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc()::fail");exit(-1);}//赋值并连接(递归)node->val = a[*pi];(*pi)++;node->left = BinaryTreeCreate(a, pi);node->right = BinaryTreeCreate(a, pi);retur
上面介绍的二叉树的一些函数的执行结果如下:
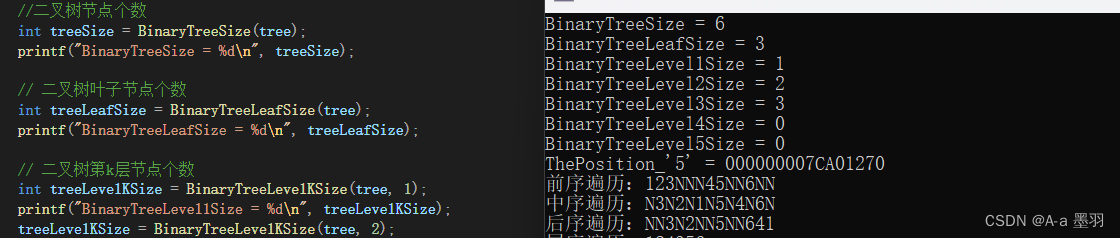
另外还有一些较为复杂的函数将在下一篇文章中介绍。