---

Bagging 算法 —— 多个基模型的聚合

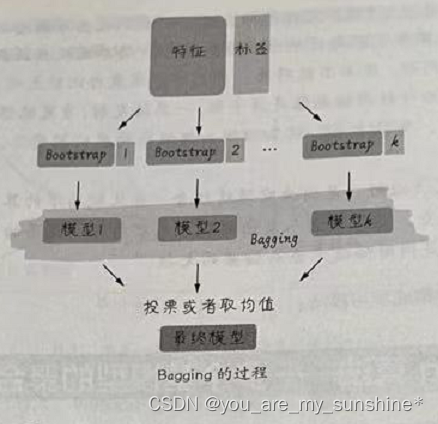
Bagging 是我们要讲的第一种集成学习算法，是Bootstrap Aggregating 的缩写。有人把它翻译为套袋法、装袋法，或者自助聚合，没有统一的叫法，就直接用它的英文名称。其算法的基本思想是从原始的数据集中抽取数据，形成K个随机的新训练集，然后训练出K个不同的模型。具体过程如下。

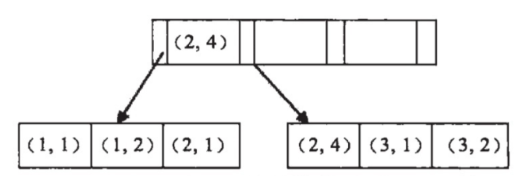
(1)从原始样本集中通过随机抽取形成K个训练集(如下图所示):每轮抽取n个训练样本(有些样本可能被多次抽取，而有些样本可能一次都没有被抽取，这叫作有放回的抽取)。这K个训练集是彼此独立的一这个过程也叫作bootstrap(可译为自举或自助采样)，它有点像K折验证但不同之处是其样本是有放回的。

(2)每次使用一个训练集通过相同的机器学习算法(如决策树、神经网络等)得到一个模型,K个训练集共得到K个模型。我们把这些模型称为基模型(base estimator ),或者基学习器。
基模型的集成有以下两种情况。

• 对于分类问题，K个模型采用投票的方式得到分类结果。
• 对于回归问题，计算K个模型的均值作为最后的结果。
  

决策树的聚合

多数情况下的Bagging，都是基于决策树的，构造随机森林的第一个步骤其实就是对多棵决策树进行Bagging，我们把它称为树的聚合(Bagging of Tree )。

树这种模型，具有显著的低偏差、高方差的特点。也就是受数据的影响特别大，一不小心，训练集准确率就接近100%了。但是这种效果不能够移植到其他的数据集。这是很明显的过拟合现象。集成学习的Bagging算法，就从树模型开始，着手解决它太过于精准，又不易泛化的问题。

当然，Bagging 的原理，并不仅限于决策树，还可以扩展到其他机器学习算法。因为通过随机抽取数据的方法减少了可能的数据干扰，所以经过Bagging 的模型将会具有低方差。

在Sklear 的集成学习库中，有BaggingClassifier和BaggingRegressor这两种Bagging模型，分别适用于分类问题和回归问题。

import numpy as np # 基础线性代数扩展包
import pandas as pd # 数据处理工具箱
df_bank = pd.read_csv("../数据集/BankCustomer.csv") # 读取文件# 构建特征和标签集合
y = df_bank['Exited']
X = df_bank.drop(['Name', 'Exited', 'City'], axis=1)from sklearn.model_selection import train_test_split # 拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 对多棵决策树进行Bagging，即树的聚合
from sklearn.ensemble import BaggingClassifier # 导入Bagging分类器
from sklearn.tree import DecisionTreeClassifier # 导入决策树分类器
from sklearn.metrics import (f1_score, confusion_matrix) # 导入评估标准
dt = BaggingClassifier(DecisionTreeClassifier()) # 只使用一棵决策树
dt.fit(X_train, y_train) # 拟合模型
y_pred = dt.predict(X_test) # 进行预测
print("决策树测试准确率: {:.2f}%".format(dt.score(X_test, y_test)*100))
print("决策树测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
bdt = BaggingClassifier(DecisionTreeClassifier()) #树的Bagging
bdt.fit(X_train, y_train) # 拟合模型
y_pred = bdt.predict(X_test) # 进行预测
print("决策树Bagging测试准确率: {:.2f}%".format(bdt.score(X_test, y_test)*100))
print("决策树Bagging测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

上面代码中的BaggingClassifier指定了DecisionTreeClassifier 决策树分类器作为基模型的类型，默认的基模型的数量是10，也就是在Bagging过程中会用Bootstrap算法生成10棵树。

在这里比较了只使用一棵决策树和经过Bagging之后的树这两种算法的预测效果，可以看到决策树 Bagging 的准确率及F1分数明显占优势。在没有调参的情况下，其验证集的F1分数达到58.76%。当然，因为Bagging 过程的随机性，每次测试的分数都稍有不同。

如果用网格搜索再进行参数优化:

from sklearn.model_selection import GridSearchCV # 导入网格搜索工具
# 使用网格搜索优化参数
bdt_param_grid = {'base_estimator__max_depth' : [5,10,20,50,100],'n_estimators' : [1, 5, 10, 50]}
bdt_gs = GridSearchCV(BaggingClassifier(DecisionTreeClassifier()),param_grid = bdt_param_grid, scoring = 'f1',n_jobs= 10, verbose = 1)
bdt_gs.fit(X_train, y_train) # 拟合模型
bdt_gs = bdt_gs.best_estimator_ # 最佳模型
y_pred = bdt.predict(X_test) # 进行预测
print("决策树Bagging测试准确率: {:.2f}%".format(bdt_gs.score(X_test, y_test)*100)) 
print("决策树Bagging测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

F1分数可能会进一步提升:

其中，base_estimator___max_depth 中的base_estimator 表示Bagging的基模型，即决策树分类器 DecisionTreeClassifier。因此，两个下划线后面的max_depth参数隶属于决策树分类器，指的是树的深度。而n_estimators参数隶属于BaggingClassifier，指的是 Bagging 过程中树的个数。
准确率为何会提升?其中的关键正是降低了模型的方差，增加了泛化能力。因为每一棵树都是在原始数据集的不同子集上进行训练的，这是以偏差的小幅增加为代价的，但是最终的模型应用于测试集后，性能会大幅提升。

从树的聚合到随机森林

当我们说到集成学习，最关键的一点是各个基模型的相关度要小，差异性要大。异质性越强，集成的效果越好。两个准确率为99%的模型，如果其预测结果都一致，也就没有提高的余地了。
那么对树的集成，关键在于这些树里面每棵树的差异性是否够大。
在树的聚合中，每一次树分叉时，都会遍历所有的特征，找到最佳的分支方案。而随机森林在此算法基础上的改善就是在树分叉时，增加了对特征选择的随机性，而并不总是考量全部的特征，这个小小的改进，就在较大程度上进一步提高了各棵树的差异。
假设树分叉时选取的特征数为m，m这个参数值通常遵循下面的规则。

• 对于分类问题，m可以设置为特征数的平方根，也就是如果特征是36，那么m大概是6。
• 对于回归问题，m可以设置为特征数的1/3，也就是如果特征是36，那么m大概是12。

在Sklearm的集成学习库中，也有RandomForestClassifier和RandomForestRegressor两种随机森林模型，分别适用于分类问题和回归问题。
下面用随机森林算法解决同样的问题，看一下预测效率:

from sklearn.ensemble import RandomForestClassifier # 导入随机森林分类器
rf = RandomForestClassifier() # 随机森林模型
# 使用网格搜索优化参数
rf_param_grid = {"max_depth": [None],"max_features": [1, 3, 10],"min_samples_split": [2, 3, 10],"min_samples_leaf": [1, 3, 10],"bootstrap": [True,False],"n_estimators" :[100,300],"criterion": ["gini"]}
rf_gs = GridSearchCV(rf,param_grid = rf_param_grid, scoring="f1", n_jobs= 10, verbose = 1)
rf_gs.fit(X_train,y_train) # 拟合模型
rf_gs = rf_gs.best_estimator_ # 最佳模型
y_pred = rf_gs.predict(X_test) # 进行预测
print("随机森林测试准确率: {:.2f}%".format(rf_gs.score(X_test, y_test)*100))
print("随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100)) 

从随机森林到极端随机森林

随机森林算法在树分叉时会随机选取m个特征作为考量，对于每一次分叉，它还是会遍历所有的分支，然后选择基于这些特征的最优分支。这本质上仍属于贪心算法(greedyeorthm),即在每一步选择中都采取在当前状态下最优的选择。而极端随机森林算法一点也不"贪心“，它甚至不去考量所有的分支，而是随机选择一些分支，从中拿到一个最优解。
下面用极端随机森林算法来解决同样的问题:

from sklearn.ensemble import ExtraTreesClassifier # 导入极端随机森林模型
ext = ExtraTreesClassifier() # 极端随机森林模型
# 使用网格搜索优化参数
ext_param_grid = {"max_depth": [None],"max_features": [1, 3, 10],"min_samples_split": [2, 3, 10],"min_samples_leaf": [1, 3, 10],"bootstrap": [True,False],"n_estimators" :[100,300],"criterion": ["gini"]}
ext_gs = GridSearchCV(ext,param_grid = ext_param_grid, scoring="f1", n_jobs= 4, verbose = 1)
ext_gs.fit(X_train,y_train) # 拟合模型
ext_gs = ext_gs.best_estimator_ # 最佳模型
y_pred = ext_gs.predict(X_test) # 进行预测
print("极端随机森林测试准确率: {:.2f}%".format(ext_gs.score(X_test, y_test)*100))
print("极端随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

关于随机森林和极端随机森林算法的性能，有以下几点需要注意。
(1)随机森林算法在绝大多数情况下是优于极端随机森林算法的。
(2)极端随机森林算法不需要考虑所有分支的可能性，所以它的运算效率往往要高于随机森林算法，也就是说速度比较快。
(3)对于某些数据集，极端随机森林算法可能拥有更强的泛化功能。但是很难知道具体什么情况下会出现这样的结果，因此不妨各种算法都试试。

---

学习机器学习的参考资料：
（1）书籍
利用Python进行数据分析
西瓜书
百面机器学习
机器学习实战
阿里云天池大赛赛题解析(机器学习篇)
白话机器学习中的数学
零基础学机器学习
图解机器学习算法
…

（2）机构
光环大数据
开课吧
极客时间
七月在线
深度之眼
贪心学院
拉勾教育
博学谷
…