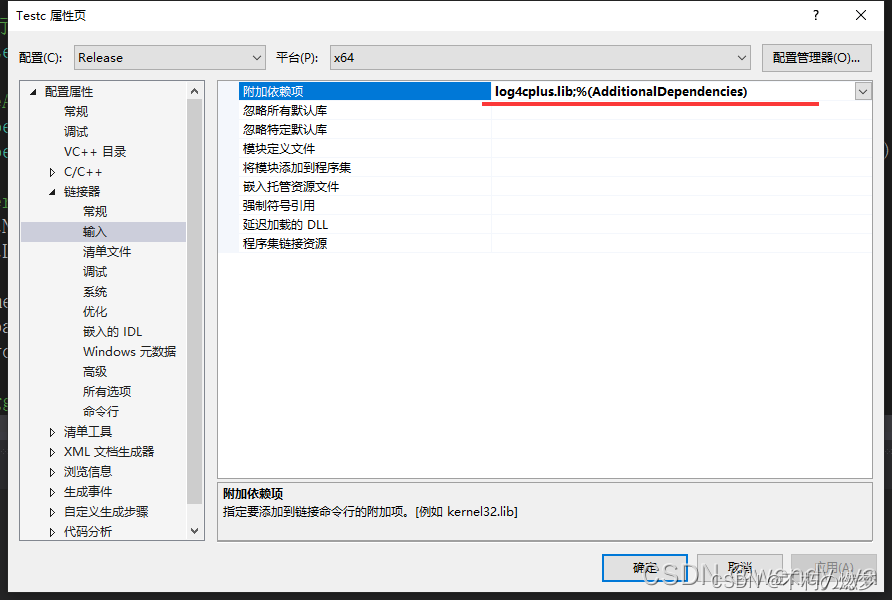
commintlint是一个npm包用来规范化我们的commit信息，当然这个行为的操作时期是在git的commit-msg生命周期期间，这一点当然是有husky来控制，需要注意的是commit-msg作为一个git生命周期会被git commit和git merge行为唤醒，并且可以通过git命令后缀跳过这一生命周期

一、准备工作

1.下载一下commitlint

npm install --save-dev @commitlint/config-conventional @commitlint/cli

 这个命令下载了两个东西，@commitlint/cli实际上是commintlint的别名，就是包的本体，@commitlint/config-convebtional实际上是默认的配置，后面会在配置表中extend字段进行注入

2.配置一下commintlint

这边的话我直接贴一下网上找来的配置，创建commitlint.config.js，并写下如下内容（网上找的，暂时看看）

export default {extends: ['@commitlint/config-conventional'],rules: {"type-enum": [2, 'always', ['feat', 'fix', 'docs', 'perf', 'revert', 'ci', 'test', 'refactor', 'build', 'style', 'chore']],'type-case': [0],//type 的输入格式,默认为小写‘lower-case’'type-empty': [0],//type 是否可为空'scope-empty': [0],//scope 是否为空'scope-case': [0],//scope 的格式,默认为小写‘lower-case’'subject-full-stop': [0, 'never'],//subject 结尾符,默认为.'subject-case': [0, 'never'],//subject 的格式，默认其中之一：['sentence-case', 'start-case', 'pascal-case', 'upper-case']'header-max-length': [0, 'always', 72]//header 最大长度，默认为72字符},};

3.创建husky的commit-msg钩子

我是分了两个步骤

npx husky add .husky/commit-msg

然后在这个钩子中写入

npx --no -- commitlint --edit

二、尝试一下写一个错误的提交

git commit -m "testhh"

看一下有什么错误

我们的commintlint果然很严格呢

三、什么才是合格的提交

我们可以看一下@commitlint/config-conventional这个默认配置的npm页面上是怎么写的

说明一下我们上面的commitlint.config.js之中配置应该是自定义部分和@commitlint/config-conventional这个配置的融合版本

下面借一张图说一下每个项的一些配置涉及什么内容

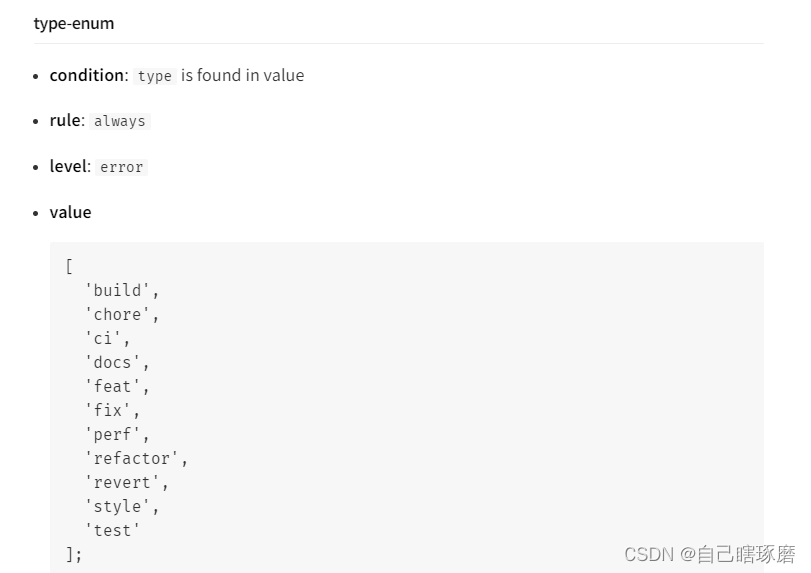
 上图是一个type-enum的配置，我们要配置的内容其实是value中的，condition代表了生效条件，也就是你的msg的类型一定要是在value之中，rule表示应该是检测的时机，这里是永远需要检测，level应该决定的是违反该规则是否报错，这样的话我们就能更好理解配置中每个内容了，这里其他配置默认配置我就不多说了。

那我们看一下我们写的commitlint.config.js里面的一些内容是啥意思

单说下面这个规则

"type-enum": [2, 'always', ['feat', 'fix', 'docs', 'perf', 'revert', 'ci', 'test','refactor', 'build', 'style', 'chore']]

type-enum我们在上面见到过，它的value是一个数组，为啥这里的值是三个呢，前面那个2和always是啥意思？

实际上每个规则都有三个参数

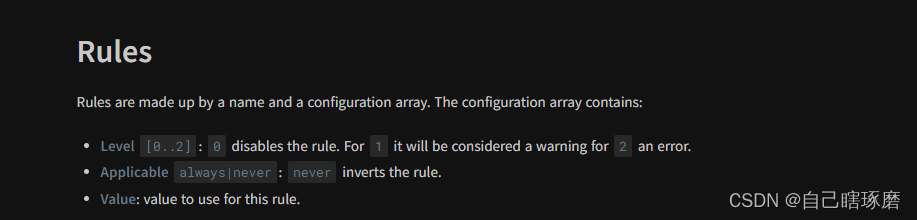
level表示层级，0表示取消该规则，1表示违反该规则会导致warning，2表示违反规则会抛出一个错误

applicable的值则表示是否逆转这个规则，如 type-enum如果第二个参数写上never，则你提交的msg的type必须不在value的范围之内。

第三个value就是正常的value。

那么我们重看上面的我们在网上找的commitlint.config.js，里面的内容实际上就是取消了@commitlint/config-conventional这个默认配置表的一些规则，这样的话，我觉得如何定制自己的配置大概就有数了。

四、一个完整的正确的提交信息例子

build: 进行一次提交测试这里是提交信息的body部分这个我不知道干什么的footer部分

注意这个“build:"后面有一个空格一定要写，你不写就提示你缺少subject

git有一个提交约定，可以看约定式提交

上面这个网页有详述 ，这样的话就可以理解上面的那些fix等等到底意味着什么，这里我就不写了